ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

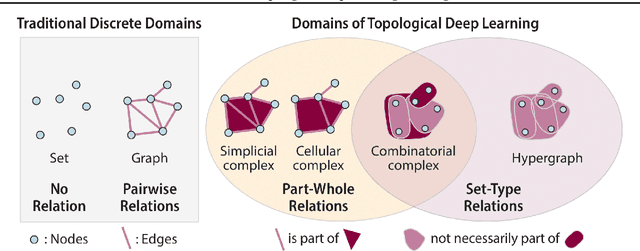
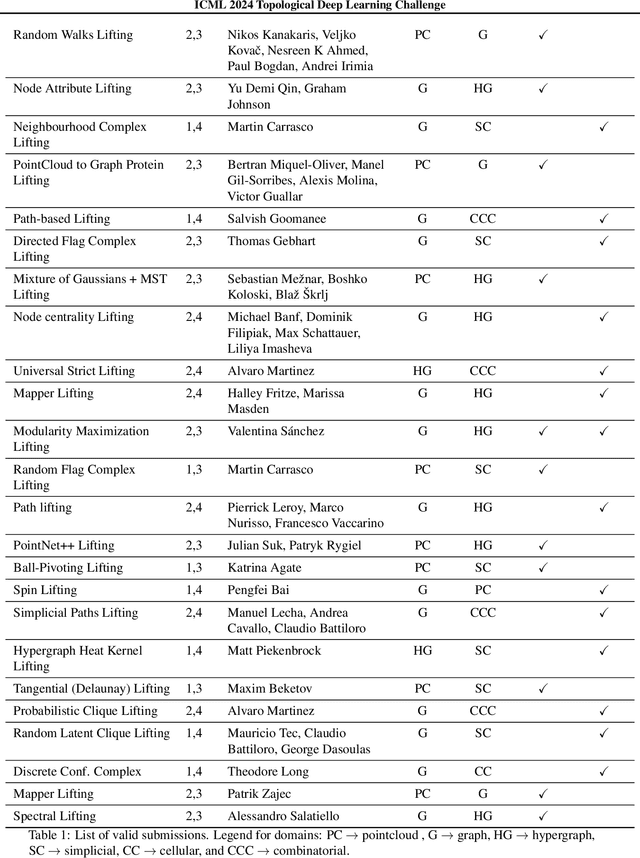
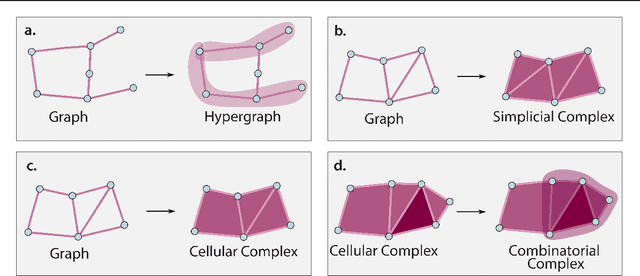
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

Global cognitive graph properties dynamics of hippocampal formation

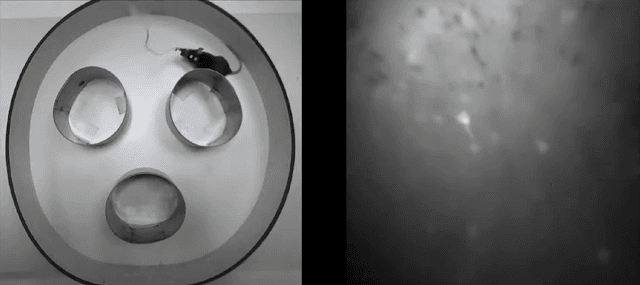
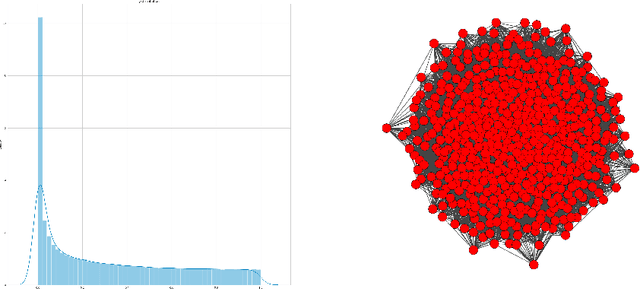
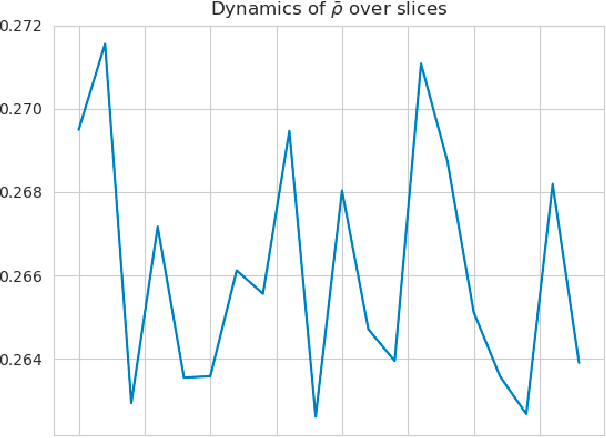
In the present study we have used a set of methods and metrics to build a graph of relative neural connections in a hippocampus of a rodent. A set of graphs was built on top of time-sequenced data and analyzed in terms of dynamics of a connection genesis. The analysis has shown that during the process of a rodent exploring a novel environment, the relations between neurons constantly change which indicates that globally memory is constantly updated even for known areas of space. Even if some neurons gain cognitive specialization, the global network though remains relatively stable. Additionally we suggest a set of methods for building a graph of cognitive neural network.

Topology of cognitive maps

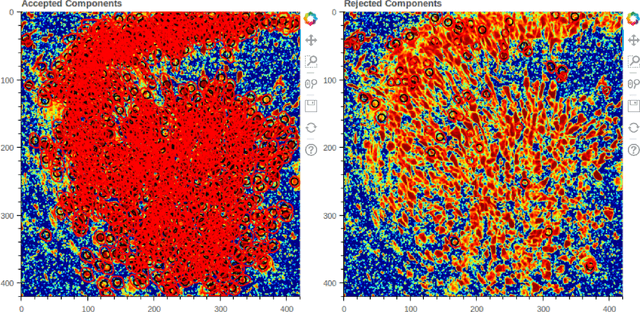
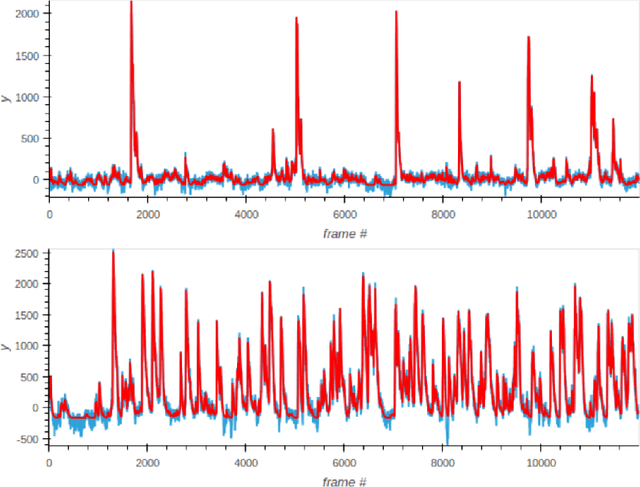
In present paper we discuss several approaches to reconstructing the topology of the physical space from neural activity data of CA1 fields in mice hippocampus, in particular, having Cognitome theory of brain function in mind. In our experiments, animals were placed in different new environments and discovered these moving freely while their physical and neural activity was recorded. We test possible approaches to identifying place cell groups out of the observed CA1 neurons. We also test and discuss various methods of dimension reduction and topology reconstruction. In particular, two main strategies we focus on are the Nerve theorem and point cloud-based methods. Conclusions on the results of reconstruction are supported with illustrations and mathematical background which is also briefly discussed.