Quiver Signal Processing (QSP)

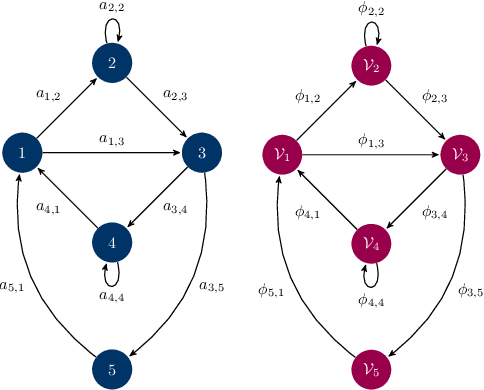
In this paper we state the basics for a signal processing framework on quiver representations. A quiver is a directed graph and a quiver representation is an assignment of vector spaces to the nodes of the graph and of linear maps between the vector spaces associated to the nodes. Leveraging the tools from representation theory, we propose a signal processing framework that allows us to handle heterogeneous multidimensional information in networks. We provide a set of examples where this framework provides a natural set of tools to understand apparently hidden structure in information. We remark that the proposed framework states the basis for building graph neural networks where information can be processed and handled in alternative ways.

Path Signatures on Lie Groups

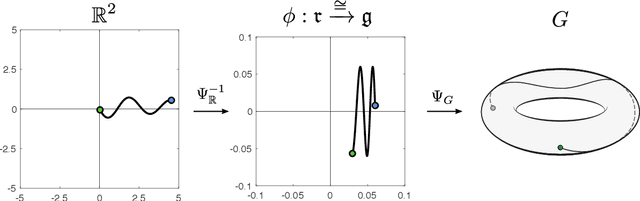
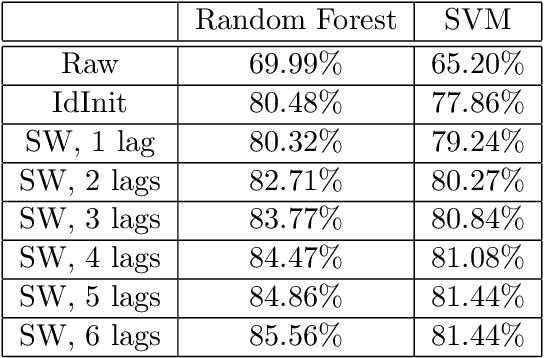
Path signatures are powerful nonparametric tools for time series analysis, shown to form a universal and characteristic feature map for Euclidean valued time series data. We lift the theory of path signatures to the setting of Lie group valued time series, adapting these tools for time series with underlying geometric constraints. We prove that this generalized path signature is universal and characteristic. To demonstrate universality, we analyze the human action recognition problem in computer vision, using $SO(3)$ representations for the time series, providing comparable performance to other shallow learning approaches, while offering an easily interpretable feature set. We also provide a two-sample hypothesis test for Lie group-valued random walks to illustrate its characteristic property. Finally we provide algorithms and a Julia implementation of these methods.

Path Homotopy Invariants and their Application to Optimal Trajectory Planning

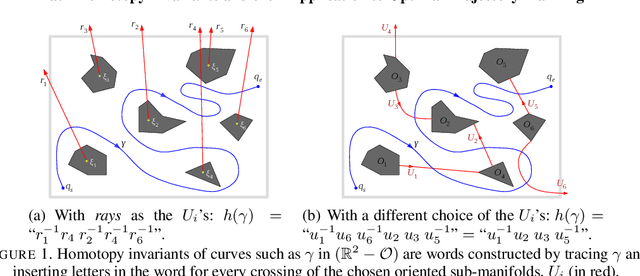
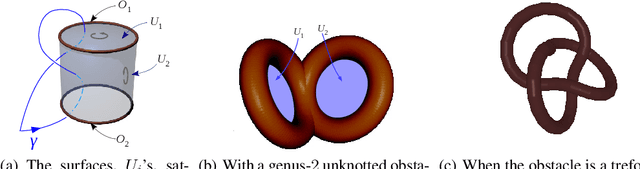
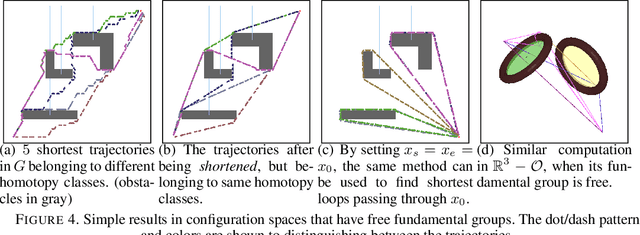
We consider the problem of optimal path planning in different homotopy classes in a given environment. Though important in robotics applications, path-planning with reasoning about homotopy classes of trajectories has typically focused on subsets of the Euclidean plane in the robotics literature. The problem of finding optimal trajectories in different homotopy classes in more general configuration spaces (or even characterizing the homotopy classes of such trajectories) can be difficult. In this paper we propose automated solutions to this problem in several general classes of configuration spaces by constructing presentations of fundamental groups and giving algorithms for solving the \emph{word problem} in such groups. We present explicit results that apply to knot and link complements in 3-space, discuss how to extend to cylindrically-deleted coordination spaces of arbitrary dimension, and also present results in the coordination space of robots navigating on an Euclidean plane.

Invariants for Homology Classes with Application to Optimal Search and Planning Problem in Robotics

We consider planning problems on a punctured Euclidean spaces, $\mathbb{R}^D - \widetilde{\mathcal{O}}$, where $\widetilde{\mathcal{O}}$ is a collection of obstacles. Such spaces are of frequent occurrence as configuration spaces of robots, where $\widetilde{\mathcal{O}}$ represent either physical obstacles that the robots need to avoid (e.g., walls, other robots, etc.) or illegal states (e.g., all legs off-the-ground). As state-planning is translated to path-planning on a configuration space, we collate equivalent plannings via topologically-equivalent paths. This prompts finding or exploring the different homology classes in such environments and finding representative optimal trajectories in each such class. In this paper we start by considering the problem of finding a complete set of easily computable homology class invariants for $(N-1)$-cycles in $(\mathbb{R}^D - \widetilde{\mathcal{O}})$. We achieve this by finding explicit generators of the $(N-1)^{st}$ de Rham cohomology group of this punctured Euclidean space, and using their integrals to define cocycles. The action of those dual cocycles on $(N-1)$-cycles gives the desired complete set of invariants. We illustrate the computation through examples. We further show that, due to the integral approach, this complete set of invariants is well-suited for efficient search-based planning of optimal robot trajectories with topological constraints. Finally we extend this approach to computation of invariants in spaces derived from $(\mathbb{R}^D - \widetilde{\mathcal{O}})$ by collapsing subspace, thereby permitting application to a wider class of non-Euclidean ambient spaces.

Safe cooperative robot dynamics on graphs

This paper initiates the use of vector fields to design, optimize, and implement reactive schedules for safe cooperative robot patterns on planar graphs. We consider Automated Guided Vehicles (AGV's) operating upon a predefined network of pathways. In contrast to the case of locally Euclidean configuration spaces, regularization of collisions is no longer a local procedure, and issues concerning the global topology of configuration spaces must be addressed. The focus of the present inquiry is the achievement of safe, efficient, cooperative patterns in the simplest nontrivial example (a pair of robots on a Y-network) by means of a state-event heirarchical controller.