Path Signatures on Lie Groups
Paper and Code
Jul 15, 2020
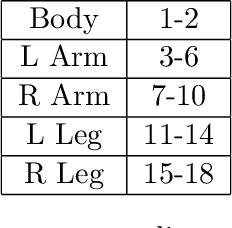
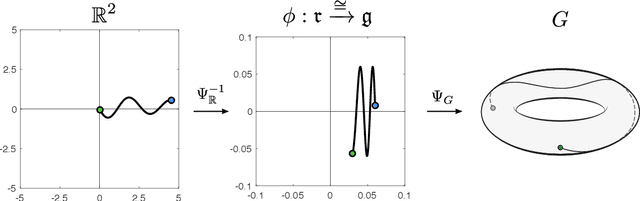
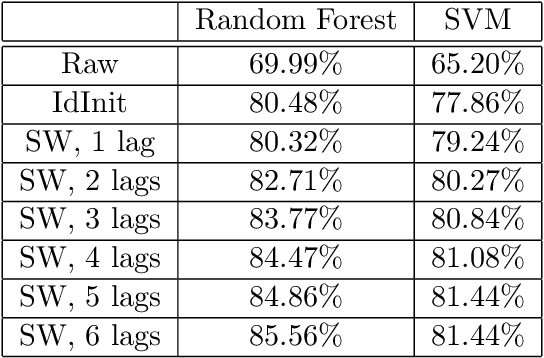
Path signatures are powerful nonparametric tools for time series analysis, shown to form a universal and characteristic feature map for Euclidean valued time series data. We lift the theory of path signatures to the setting of Lie group valued time series, adapting these tools for time series with underlying geometric constraints. We prove that this generalized path signature is universal and characteristic. To demonstrate universality, we analyze the human action recognition problem in computer vision, using $SO(3)$ representations for the time series, providing comparable performance to other shallow learning approaches, while offering an easily interpretable feature set. We also provide a two-sample hypothesis test for Lie group-valued random walks to illustrate its characteristic property. Finally we provide algorithms and a Julia implementation of these methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge