Towards Scalable Topological Regularizers

Latent space matching, which consists of matching distributions of features in latent space, is a crucial component for tasks such as adversarial attacks and defenses, domain adaptation, and generative modelling. Metrics for probability measures, such as Wasserstein and maximum mean discrepancy, are commonly used to quantify the differences between such distributions. However, these are often costly to compute, or do not appropriately take the geometric and topological features of the distributions into consideration. Persistent homology is a tool from topological data analysis which quantifies the multi-scale topological structure of point clouds, and has recently been used as a topological regularizer in learning tasks. However, computation costs preclude larger scale computations, and discontinuities in the gradient lead to unstable training behavior such as in adversarial tasks. We propose the use of principal persistence measures, based on computing the persistent homology of a large number of small subsamples, as a topological regularizer. We provide a parallelized GPU implementation of this regularizer, and prove that gradients are continuous for smooth densities. Furthermore, we demonstrate the efficacy of this regularizer on shape matching, image generation, and semi-supervised learning tasks, opening the door towards a scalable regularizer for topological features.

Ergodic Trajectory Optimization on Generalized Domains Using Maximum Mean Discrepancy

We present a novel formulation of ergodic trajectory optimization that can be specified over general domains using kernel maximum mean discrepancy. Ergodic trajectory optimization is an effective approach that generates coverage paths for problems related to robotic inspection, information gathering problems, and search and rescue. These optimization schemes compel the robot to spend time in a region proportional to the expected utility of visiting that region. Current methods for ergodic trajectory optimization rely on domain-specific knowledge, e.g., a defined utility map, and well-defined spatial basis functions to produce ergodic trajectories. Here, we present a generalization of ergodic trajectory optimization based on maximum mean discrepancy that requires only samples from the search domain. We demonstrate the ability of our approach to produce coverage trajectories on a variety of problem domains including robotic inspection of objects with differential kinematics constraints and on Lie groups without having access to domain specific knowledge. Furthermore, we show favorable computational scaling compared to existing state-of-the-art methods for ergodic trajectory optimization with a trade-off between domain specific knowledge and computational scaling, thus extending the versatility of ergodic coverage on a wider application domain.

Stein Variational Ergodic Search

Exploration requires that robots reason about numerous ways to cover a space in response to dynamically changing conditions. However, in continuous domains there are potentially infinitely many options for robots to explore which can prove computationally challenging. How then should a robot efficiently optimize and choose exploration strategies to adopt? In this work, we explore this question through the use of variational inference to efficiently solve for distributions of coverage trajectories. Our approach leverages ergodic search methods to optimize coverage trajectories in continuous time and space. In order to reason about distributions of trajectories, we formulate ergodic search as a probabilistic inference problem. We propose to leverage Stein variational methods to approximate a posterior distribution over ergodic trajectories through parallel computation. As a result, it becomes possible to efficiently optimize distributions of feasible coverage trajectories for which robots can adapt exploration. We demonstrate that the proposed Stein variational ergodic search approach facilitates efficient identification of multiple coverage strategies and show online adaptation in a model-predictive control formulation. Simulated and physical experiments demonstrate adaptability and diversity in exploration strategies online.

The Signature Kernel

The signature kernel is a positive definite kernel for sequential data. It inherits theoretical guarantees from stochastic analysis, has efficient algorithms for computation, and shows strong empirical performance. In this short survey paper for a forthcoming Springer handbook, we give an elementary introduction to the signature kernel and highlight these theoretical and computational properties.

Capturing Graphs with Hypo-Elliptic Diffusions

Convolutional layers within graph neural networks operate by aggregating information about local neighbourhood structures; one common way to encode such substructures is through random walks. The distribution of these random walks evolves according to a diffusion equation defined using the graph Laplacian. We extend this approach by leveraging classic mathematical results about hypo-elliptic diffusions. This results in a novel tensor-valued graph operator, which we call the hypo-elliptic graph Laplacian. We provide theoretical guarantees and efficient low-rank approximation algorithms. In particular, this gives a structured approach to capture long-range dependencies on graphs that is robust to pooling. Besides the attractive theoretical properties, our experiments show that this method competes with graph transformers on datasets requiring long-range reasoning but scales only linearly in the number of edges as opposed to quadratically in nodes.

Path Signatures on Lie Groups

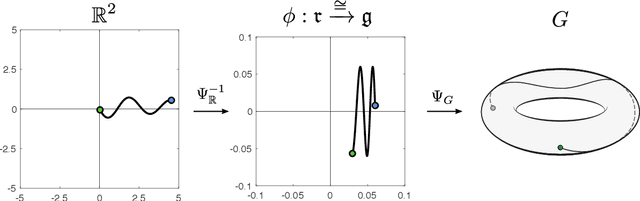
Path signatures are powerful nonparametric tools for time series analysis, shown to form a universal and characteristic feature map for Euclidean valued time series data. We lift the theory of path signatures to the setting of Lie group valued time series, adapting these tools for time series with underlying geometric constraints. We prove that this generalized path signature is universal and characteristic. To demonstrate universality, we analyze the human action recognition problem in computer vision, using $SO(3)$ representations for the time series, providing comparable performance to other shallow learning approaches, while offering an easily interpretable feature set. We also provide a two-sample hypothesis test for Lie group-valued random walks to illustrate its characteristic property. Finally we provide algorithms and a Julia implementation of these methods.