Celia Hacker
Simplicial Representation Learning with Neural $k$-forms
Dec 13, 2023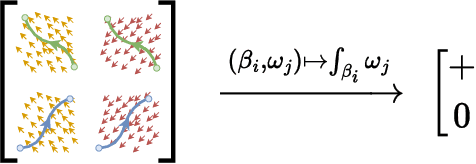

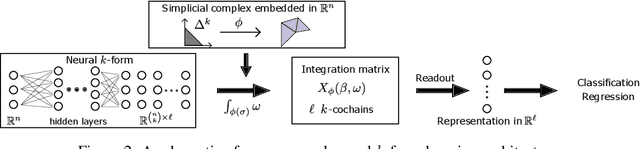

Abstract:Geometric deep learning extends deep learning to incorporate information about the geometry and topology data, especially in complex domains like graphs. Despite the popularity of message passing in this field, it has limitations such as the need for graph rewiring, ambiguity in interpreting data, and over-smoothing. In this paper, we take a different approach, focusing on leveraging geometric information from simplicial complexes embedded in $\mathbb{R}^n$ using node coordinates. We use differential k-forms in \mathbb{R}^n to create representations of simplices, offering interpretability and geometric consistency without message passing. This approach also enables us to apply differential geometry tools and achieve universal approximation. Our method is efficient, versatile, and applicable to various input complexes, including graphs, simplicial complexes, and cell complexes. It outperforms existing message passing neural networks in harnessing information from geometrical graphs with node features serving as coordinates.
On the Surprising Behaviour of node2vec
Jun 16, 2022
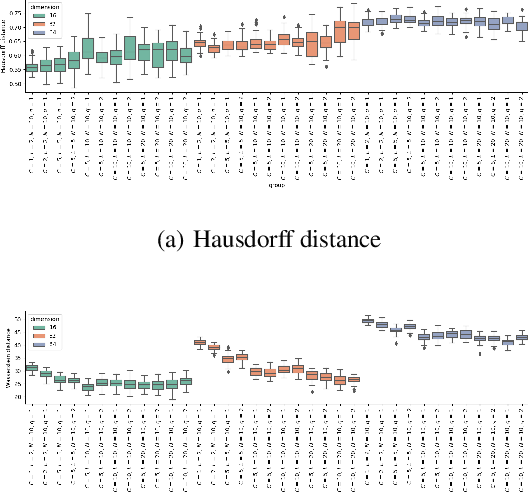
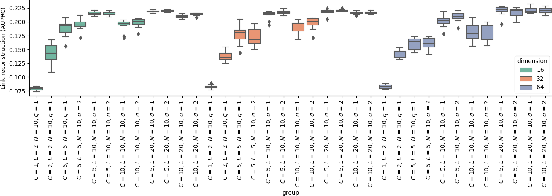
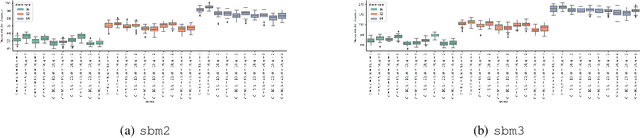
Abstract:Graph embedding techniques are a staple of modern graph learning research. When using embeddings for downstream tasks such as classification, information about their stability and robustness, i.e., their susceptibility to sources of noise, stochastic effects, or specific parameter choices, becomes increasingly important. As one of the most prominent graph embedding schemes, we focus on node2vec and analyse its embedding quality from multiple perspectives. Our findings indicate that embedding quality is unstable with respect to parameter choices, and we propose strategies to remedy this in practice.
Capturing Graphs with Hypo-Elliptic Diffusions
May 27, 2022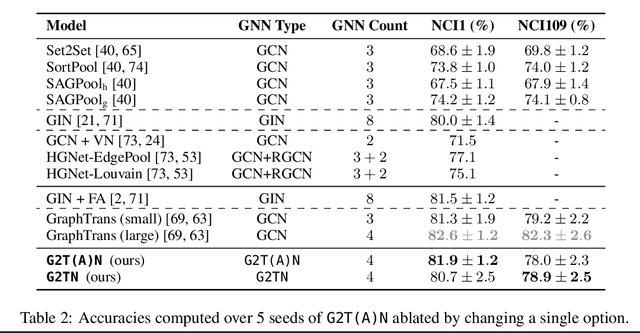



Abstract:Convolutional layers within graph neural networks operate by aggregating information about local neighbourhood structures; one common way to encode such substructures is through random walks. The distribution of these random walks evolves according to a diffusion equation defined using the graph Laplacian. We extend this approach by leveraging classic mathematical results about hypo-elliptic diffusions. This results in a novel tensor-valued graph operator, which we call the hypo-elliptic graph Laplacian. We provide theoretical guarantees and efficient low-rank approximation algorithms. In particular, this gives a structured approach to capture long-range dependencies on graphs that is robust to pooling. Besides the attractive theoretical properties, our experiments show that this method competes with graph transformers on datasets requiring long-range reasoning but scales only linearly in the number of edges as opposed to quadratically in nodes.
k-simplex2vec: a simplicial extension of node2vec
Oct 12, 2020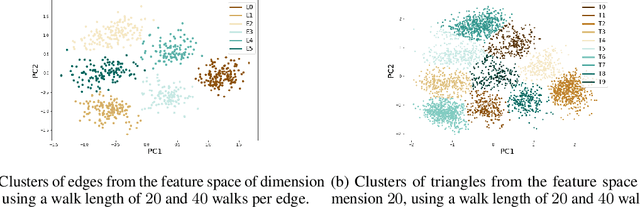
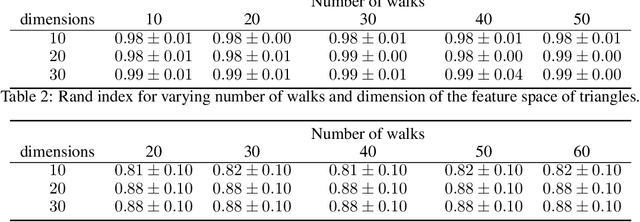
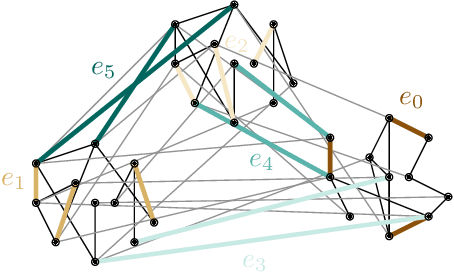
Abstract:We present a novel method of associating Euclidean features to simplicial complexes, providing a way to use them as input to statistical and machine learning tools. This method extends the node2vec algorithm to simplices of higher dimensions, providing insight into the structure of a simplicial complex, or into the higher-order interactions in a graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge