Random Fourier Signature Features

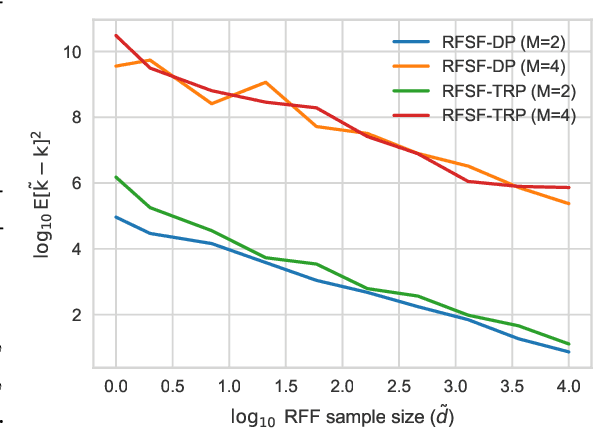
Tensor algebras give rise to one of the most powerful measures of similarity for sequences of arbitrary length called the signature kernel accompanied with attractive theoretical guarantees from stochastic analysis. Previous algorithms to compute the signature kernel scale quadratically in terms of the length and the number of the sequences. To mitigate this severe computational bottleneck, we develop a random Fourier feature-based acceleration of the signature kernel acting on the inherently non-Euclidean domain of sequences. We show uniform approximation guarantees for the proposed unbiased estimator of the signature kernel, while keeping its computation linear in the sequence length and number. In addition, combined with recent advances on tensor projections, we derive two even more scalable time series features with favourable concentration properties and computational complexity both in time and memory. Our empirical results show that the reduction in computational cost comes at a negligible price in terms of accuracy on moderate-sized datasets, and it enables one to scale to large datasets up to a million time series.

Capturing Graphs with Hypo-Elliptic Diffusions

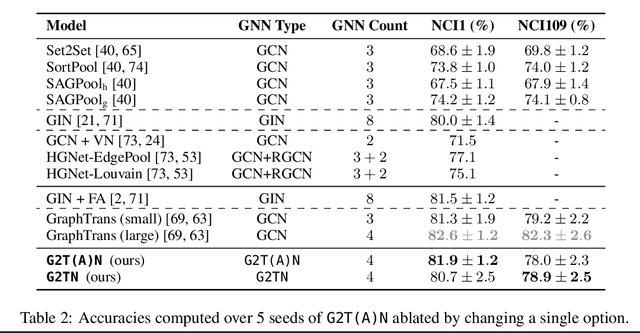
Convolutional layers within graph neural networks operate by aggregating information about local neighbourhood structures; one common way to encode such substructures is through random walks. The distribution of these random walks evolves according to a diffusion equation defined using the graph Laplacian. We extend this approach by leveraging classic mathematical results about hypo-elliptic diffusions. This results in a novel tensor-valued graph operator, which we call the hypo-elliptic graph Laplacian. We provide theoretical guarantees and efficient low-rank approximation algorithms. In particular, this gives a structured approach to capture long-range dependencies on graphs that is robust to pooling. Besides the attractive theoretical properties, our experiments show that this method competes with graph transformers on datasets requiring long-range reasoning but scales only linearly in the number of edges as opposed to quadratically in nodes.

Seq2Tens: An Efficient Representation of Sequences by Low-Rank Tensor Projections

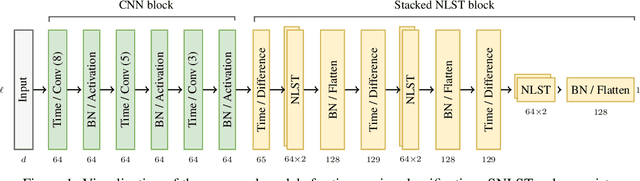
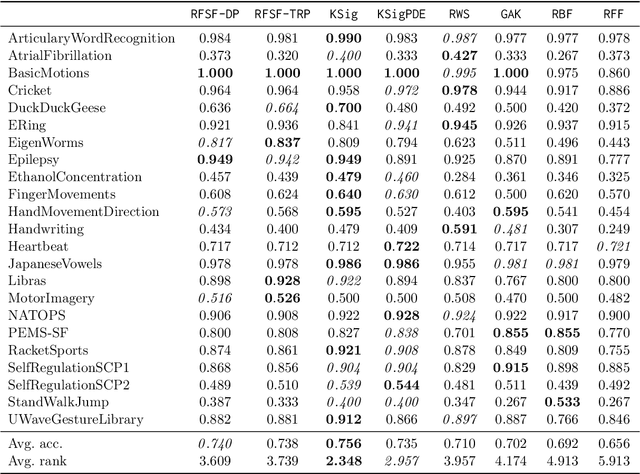
Sequential data such as time series, video, or text can be challenging to analyse as the ordered structure gives rise to complex dependencies. At the heart of this is non-commutativity, in the sense that reordering the elements of a sequence can completely change its meaning. We use a classical mathematical object -- the tensor algebra -- to capture such dependencies. To address the innate computational complexity of high degree tensors, we use compositions of low-rank tensor projections. This yields modular and scalable building blocks for neural networks that give state-of-the-art performance on standard benchmarks such as multivariate time series classification and generative models for video.

Variational Gaussian Processes with Signature Covariances

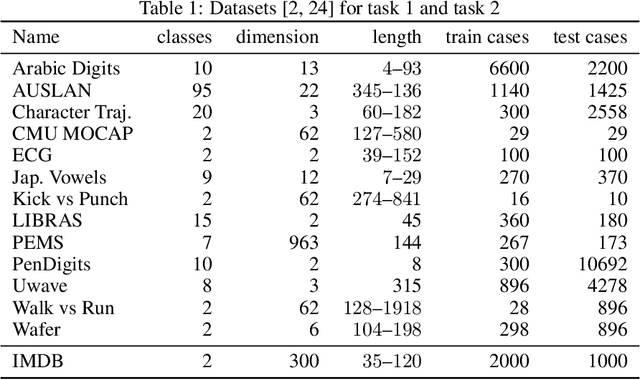
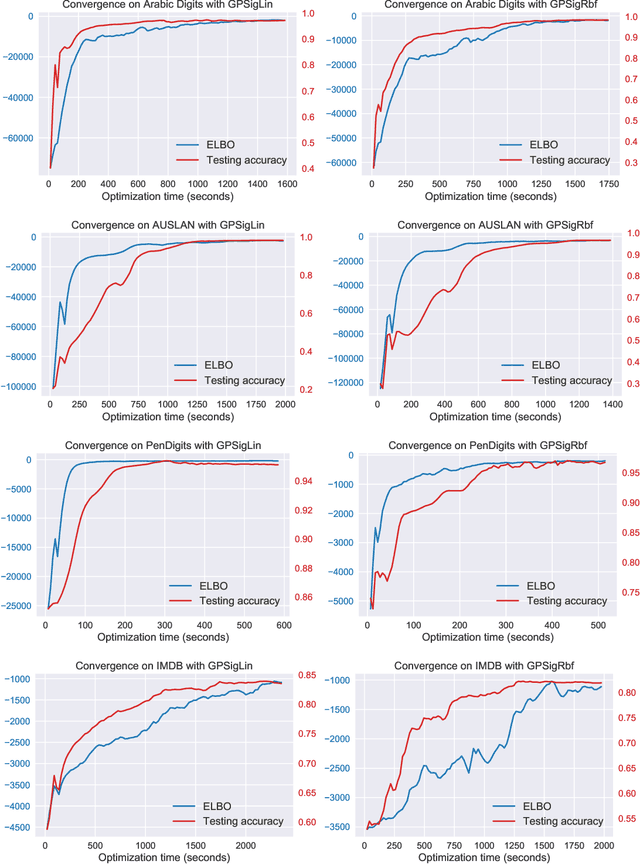
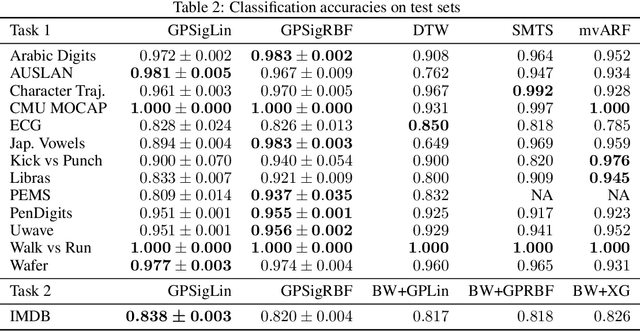
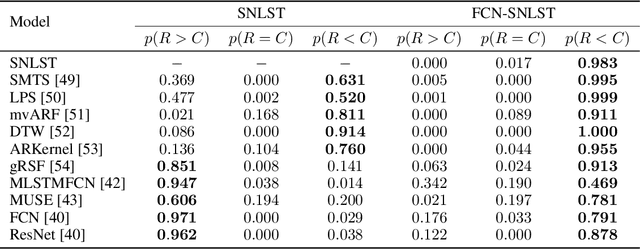
We introduce a Bayesian approach to learn from stream-valued data by using Gaussian processes with the recently introduced signature kernel as covariance function. To cope with the computational complexity in time and memory that arises with long streams that evolve in large state spaces, we develop a variational Bayes approach with sparse inducing tensors. We provide an implementation based on GPFlow and benchmark this variational Gaussian process model on supervised classification tasks for time series and text (a stream of words).