Grammar-based Ordinary Differential Equation Discovery

The understanding and modeling of complex physical phenomena through dynamical systems has historically driven scientific progress, as it provides the tools for predicting the behavior of different systems under diverse conditions through time. The discovery of dynamical systems has been indispensable in engineering, as it allows for the analysis and prediction of complex behaviors for computational modeling, diagnostics, prognostics, and control of engineered systems. Joining recent efforts that harness the power of symbolic regression in this domain, we propose a novel framework for the end-to-end discovery of ordinary differential equations (ODEs), termed Grammar-based ODE Discovery Engine (GODE). The proposed methodology combines formal grammars with dimensionality reduction and stochastic search for efficiently navigating high-dimensional combinatorial spaces. Grammars allow us to seed domain knowledge and structure for both constraining, as well as, exploring the space of candidate expressions. GODE proves to be more sample- and parameter-efficient than state-of-the-art transformer-based models and to discover more accurate and parsimonious ODE expressions than both genetic programming- and other grammar-based methods for more complex inference tasks, such as the discovery of structural dynamics. Thus, we introduce a tool that could play a catalytic role in dynamics discovery tasks, including modeling, system identification, and monitoring tasks.

Neuro-Symbolic AI for Analytical Solutions of Differential Equations

Analytical solutions of differential equations offer exact insights into fundamental behaviors of physical processes. Their application, however, is limited as finding these solutions is difficult. To overcome this limitation, we combine two key insights. First, constructing an analytical solution requires a composition of foundational solution components. Second, iterative solvers define parameterized function spaces with constraint-based updates. Our approach merges compositional differential equation solution techniques with iterative refinement by using formal grammars, building a rich space of candidate solutions that are embedded into a low-dimensional (continuous) latent manifold for probabilistic exploration. This integration unifies numerical and symbolic differential equation solvers via a neuro-symbolic AI framework to find analytical solutions of a wide variety of differential equations. By systematically constructing candidate expressions and applying constraint-based refinement, we overcome longstanding barriers to extract such closed-form solutions. We illustrate advantages over commercial solvers, symbolic methods, and approximate neural networks on a diverse set of problems, demonstrating both generality and accuracy.

Accelerated Patient-Specific Calibration via Differentiable Hemodynamics Simulations

One of the goals of personalized medicine is to tailor diagnostics to individual patients. Diagnostics are performed in practice by measuring quantities, called biomarkers, that indicate the existence and progress of a disease. In common cardiovascular diseases, such as hypertension, biomarkers that are closely related to the clinical representation of a patient can be predicted using computational models. Personalizing computational models translates to considering patient-specific flow conditions, for example, the compliance of blood vessels that cannot be a priori known and quantities such as the patient geometry that can be measured using imaging. Therefore, a patient is identified by a set of measurable and nonmeasurable parameters needed to well-define a computational model; else, the computational model is not personalized, meaning it is prone to large prediction errors. Therefore, to personalize a computational model, sufficient information needs to be extracted from the data. The current methods by which this is done are either inefficient, due to relying on slow-converging optimization methods, or hard to interpret, due to using `black box` deep-learning algorithms. We propose a personalized diagnostic procedure based on a differentiable 0D-1D Navier-Stokes reduced order model solver and fast parameter inference methods that take advantage of gradients through the solver. By providing a faster method for performing parameter inference and sensitivity analysis through differentiability while maintaining the interpretability of well-understood mathematical models and numerical methods, the best of both worlds is combined. The performance of the proposed solver is validated against a well-established process on different geometries, and different parameter inference processes are successfully performed.

FUSE: Fast Unified Simulation and Estimation for PDEs

The joint prediction of continuous fields and statistical estimation of the underlying discrete parameters is a common problem for many physical systems, governed by PDEs. Hitherto, it has been separately addressed by employing operator learning surrogates for field prediction while using simulation-based inference (and its variants) for statistical parameter determination. Here, we argue that solving both problems within the same framework can lead to consistent gains in accuracy and robustness. To this end, We propose a novel and flexible formulation of the operator learning problem that allows jointly predicting continuous quantities and inferring distributions of discrete parameters, and thus amortizing the cost of both the inverse and the surrogate models to a joint pre-training step. We present the capabilities of the proposed methodology for predicting continuous and discrete biomarkers in full-body haemodynamics simulations under different levels of missing information. We also consider a test case for atmospheric large-eddy simulation of a two-dimensional dry cold bubble, where we infer both continuous time-series and information about the systems conditions. We present comparisons against different baselines to showcase significantly increased accuracy in both the inverse and the surrogate tasks.

Variational Autoencoding Neural Operators

Unsupervised learning with functional data is an emerging paradigm of machine learning research with applications to computer vision, climate modeling and physical systems. A natural way of modeling functional data is by learning operators between infinite dimensional spaces, leading to discretization invariant representations that scale independently of the sample grid resolution. Here we present Variational Autoencoding Neural Operators (VANO), a general strategy for making a large class of operator learning architectures act as variational autoencoders. For this purpose, we provide a novel rigorous mathematical formulation of the variational objective in function spaces for training. VANO first maps an input function to a distribution over a latent space using a parametric encoder and then decodes a sample from the latent distribution to reconstruct the input, as in classic variational autoencoders. We test VANO with different model set-ups and architecture choices for a variety of benchmarks. We start from a simple Gaussian random field where we can analytically track what the model learns and progressively transition to more challenging benchmarks including modeling phase separation in Cahn-Hilliard systems and real world satellite data for measuring Earth surface deformation.

NOMAD: Nonlinear Manifold Decoders for Operator Learning

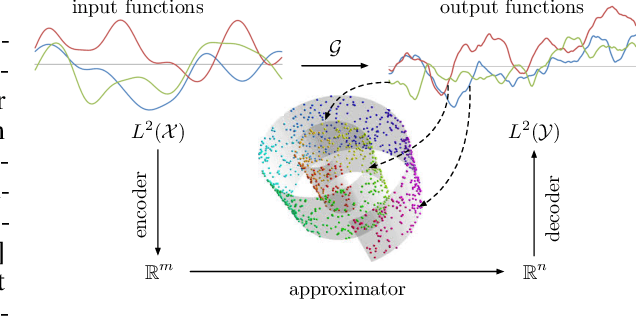
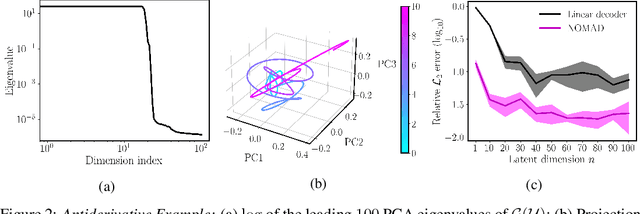
Supervised learning in function spaces is an emerging area of machine learning research with applications to the prediction of complex physical systems such as fluid flows, solid mechanics, and climate modeling. By directly learning maps (operators) between infinite dimensional function spaces, these models are able to learn discretization invariant representations of target functions. A common approach is to represent such target functions as linear combinations of basis elements learned from data. However, there are simple scenarios where, even though the target functions form a low dimensional submanifold, a very large number of basis elements is needed for an accurate linear representation. Here we present NOMAD, a novel operator learning framework with a nonlinear decoder map capable of learning finite dimensional representations of nonlinear submanifolds in function spaces. We show this method is able to accurately learn low dimensional representations of solution manifolds to partial differential equations while outperforming linear models of larger size. Additionally, we compare to state-of-the-art operator learning methods on a complex fluid dynamics benchmark and achieve competitive performance with a significantly smaller model size and training cost.

Scalable Uncertainty Quantification for Deep Operator Networks using Randomized Priors

We present a simple and effective approach for posterior uncertainty quantification in deep operator networks (DeepONets); an emerging paradigm for supervised learning in function spaces. We adopt a frequentist approach based on randomized prior ensembles, and put forth an efficient vectorized implementation for fast parallel inference on accelerated hardware. Through a collection of representative examples in computational mechanics and climate modeling, we show that the merits of the proposed approach are fourfold. (1) It can provide more robust and accurate predictions when compared against deterministic DeepONets. (2) It shows great capability in providing reliable uncertainty estimates on scarce data-sets with multi-scale function pairs. (3) It can effectively detect out-of-distribution and adversarial examples. (4) It can seamlessly quantify uncertainty due to model bias, as well as noise corruption in the data. Finally, we provide an optimized JAX library called {\em UQDeepONet} that can accommodate large model architectures, large ensemble sizes, as well as large data-sets with excellent parallel performance on accelerated hardware, thereby enabling uncertainty quantification for DeepONets in realistic large-scale applications.

Learning Operators with Coupled Attention

Supervised operator learning is an emerging machine learning paradigm with applications to modeling the evolution of spatio-temporal dynamical systems and approximating general black-box relationships between functional data. We propose a novel operator learning method, LOCA (Learning Operators with Coupled Attention), motivated from the recent success of the attention mechanism. In our architecture, the input functions are mapped to a finite set of features which are then averaged with attention weights that depend on the output query locations. By coupling these attention weights together with an integral transform, LOCA is able to explicitly learn correlations in the target output functions, enabling us to approximate nonlinear operators even when the number of output function in the training set measurements is very small. Our formulation is accompanied by rigorous approximation theoretic guarantees on the universal expressiveness of the proposed model. Empirically, we evaluate the performance of LOCA on several operator learning scenarios involving systems governed by ordinary and partial differential equations, as well as a black-box climate prediction problem. Through these scenarios we demonstrate state of the art accuracy, robustness with respect to noisy input data, and a consistently small spread of errors over testing data sets, even for out-of-distribution prediction tasks.

Machine learning in cardiovascular flows modeling: Predicting pulse wave propagation from non-invasive clinical measurements using physics-informed deep learning

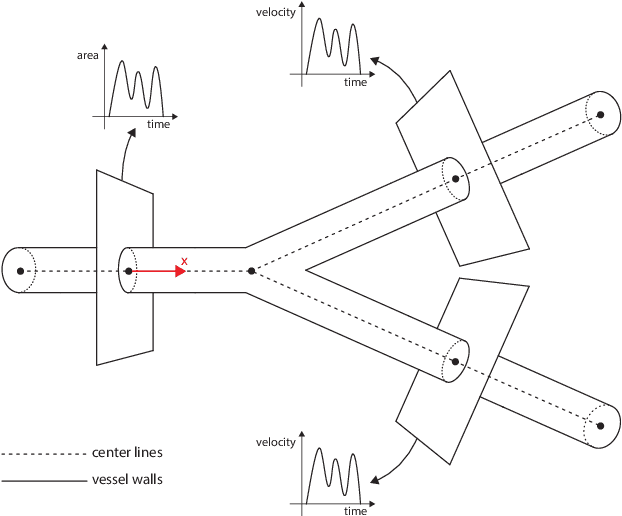
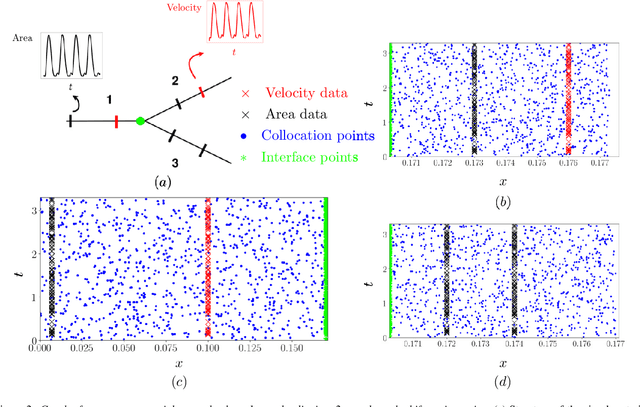
Advances in computational science offer a principled pipeline for predictive modeling of cardiovascular flows and aspire to provide a valuable tool for monitoring, diagnostics and surgical planning. Such models can be nowadays deployed on large patient-specific topologies of systemic arterial networks and return detailed predictions on flow patterns, wall shear stresses, and pulse wave propagation. However, their success heavily relies on tedious pre-processing and calibration procedures that typically induce a significant computational cost, thus hampering their clinical applicability. In this work we put forth a machine learning framework that enables the seamless synthesis of non-invasive in-vivo measurement techniques and computational flow dynamics models derived from first physical principles. We illustrate this new paradigm by showing how one-dimensional models of pulsatile flow can be used to constrain the output of deep neural networks such that their predictions satisfy the conservation of mass and momentum principles. Once trained on noisy and scattered clinical data of flow and wall displacement, these networks can return physically consistent predictions for velocity, pressure and wall displacement pulse wave propagation, all without the need to employ conventional simulators. A simple post-processing of these outputs can also provide a cheap and effective way for estimating Windkessel model parameters that are required for the calibration of traditional computational models. The effectiveness of the proposed techniques is demonstrated through a series of prototype benchmarks, as well as a realistic clinical case involving in-vivo measurements near the aorta/carotid bifurcation of a healthy human subject.