Adapting Vision-Language Models Without Labels: A Comprehensive Survey

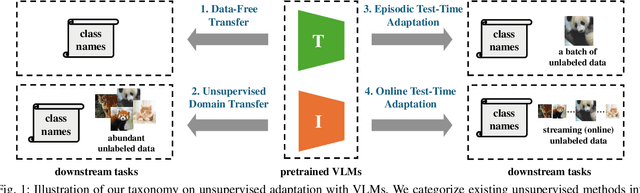
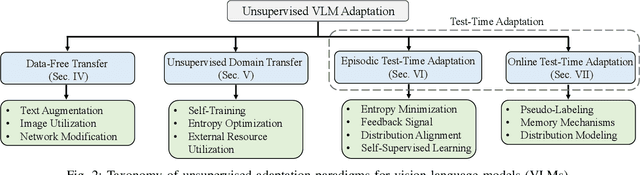
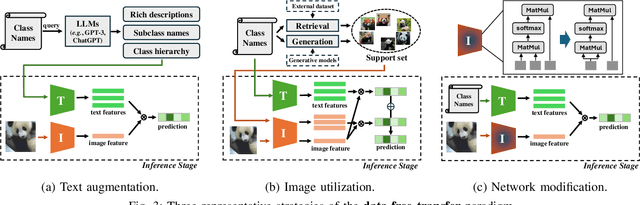
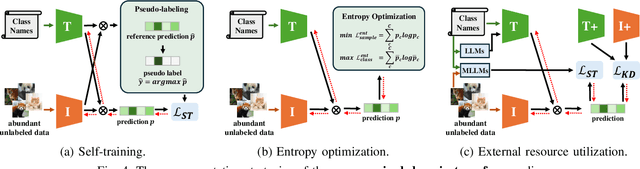
Vision-Language Models (VLMs) have demonstrated remarkable generalization capabilities across a wide range of tasks. However, their performance often remains suboptimal when directly applied to specific downstream scenarios without task-specific adaptation. To enhance their utility while preserving data efficiency, recent research has increasingly focused on unsupervised adaptation methods that do not rely on labeled data. Despite the growing interest in this area, there remains a lack of a unified, task-oriented survey dedicated to unsupervised VLM adaptation. To bridge this gap, we present a comprehensive and structured overview of the field. We propose a taxonomy based on the availability and nature of unlabeled visual data, categorizing existing approaches into four key paradigms: Data-Free Transfer (no data), Unsupervised Domain Transfer (abundant data), Episodic Test-Time Adaptation (batch data), and Online Test-Time Adaptation (streaming data). Within this framework, we analyze core methodologies and adaptation strategies associated with each paradigm, aiming to establish a systematic understanding of the field. Additionally, we review representative benchmarks across diverse applications and highlight open challenges and promising directions for future research. An actively maintained repository of relevant literature is available at https://github.com/tim-learn/Awesome-LabelFree-VLMs.

Beyond Static Models: Hypernetworks for Adaptive and Generalizable Forecasting in Complex Parametric Dynamical Systems

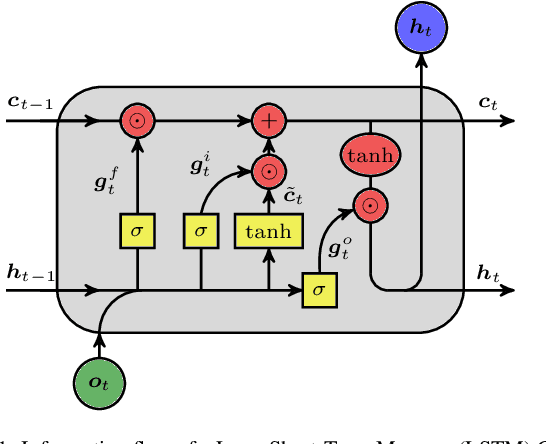
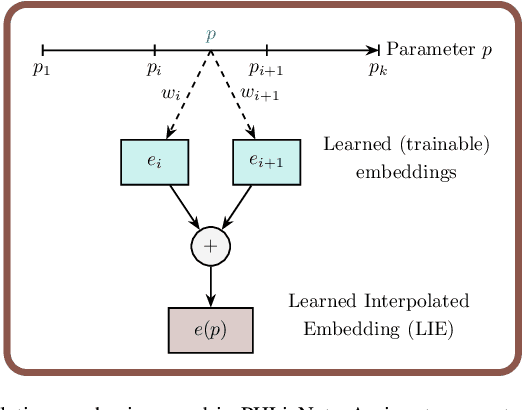
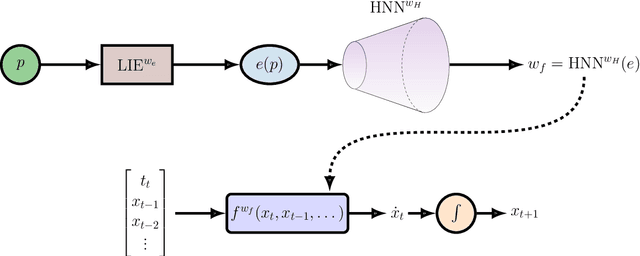
Dynamical systems play a key role in modeling, forecasting, and decision-making across a wide range of scientific domains. However, variations in system parameters, also referred to as parametric variability, can lead to drastically different model behavior and output, posing challenges for constructing models that generalize across parameter regimes. In this work, we introduce the Parametric Hypernetwork for Learning Interpolated Networks (PHLieNet), a framework that simultaneously learns: (a) a global mapping from the parameter space to a nonlinear embedding and (b) a mapping from the inferred embedding to the weights of a dynamics propagation network. The learned embedding serves as a latent representation that modulates a base network, termed the hypernetwork, enabling it to generate the weights of a target network responsible for forecasting the system's state evolution conditioned on the previous time history. By interpolating in the space of models rather than observations, PHLieNet facilitates smooth transitions across parameterized system behaviors, enabling a unified model that captures the dynamic behavior across a broad range of system parameterizations. The performance of the proposed technique is validated in a series of dynamical systems with respect to its ability to extrapolate in time and interpolate and extrapolate in the parameter space, i.e., generalize to dynamics that were unseen during training. In all cases, our approach outperforms or matches state-of-the-art baselines in both short-term forecast accuracy and in capturing long-term dynamical features, such as attractor statistics.

Automating Traffic Monitoring with SHM Sensor Networks via Vision-Supervised Deep Learning

Bridges, as critical components of civil infrastructure, are increasingly affected by deterioration, making reliable traffic monitoring essential for assessing their remaining service life. Among operational loads, traffic load plays a pivotal role, and recent advances in deep learning - particularly in computer vision (CV) - have enabled progress toward continuous, automated monitoring. However, CV-based approaches suffer from limitations, including privacy concerns and sensitivity to lighting conditions, while traditional non-vision-based methods often lack flexibility in deployment and validation. To bridge this gap, we propose a fully automated deep-learning pipeline for continuous traffic monitoring using structural health monitoring (SHM) sensor networks. Our approach integrates CV-assisted high-resolution dataset generation with supervised training and inference, leveraging graph neural networks (GNNs) to capture the spatial structure and interdependence of sensor data. By transferring knowledge from CV outputs to SHM sensors, the proposed framework enables sensor networks to achieve comparable accuracy of vision-based systems, with minimal human intervention. Applied to accelerometer and strain gauge data in a real-world case study, the model achieves state-of-the-art performance, with classification accuracies of 99% for light vehicles and 94% for heavy vehicles.

To Trust Or Not To Trust Your Vision-Language Model's Prediction

Vision-Language Models (VLMs) have demonstrated strong capabilities in aligning visual and textual modalities, enabling a wide range of applications in multimodal understanding and generation. While they excel in zero-shot and transfer learning scenarios, VLMs remain susceptible to misclassification, often yielding confident yet incorrect predictions. This limitation poses a significant risk in safety-critical domains, where erroneous predictions can lead to severe consequences. In this work, we introduce TrustVLM, a training-free framework designed to address the critical challenge of estimating when VLM's predictions can be trusted. Motivated by the observed modality gap in VLMs and the insight that certain concepts are more distinctly represented in the image embedding space, we propose a novel confidence-scoring function that leverages this space to improve misclassification detection. We rigorously evaluate our approach across 17 diverse datasets, employing 4 architectures and 2 VLMs, and demonstrate state-of-the-art performance, with improvements of up to 51.87% in AURC, 9.14% in AUROC, and 32.42% in FPR95 compared to existing baselines. By improving the reliability of the model without requiring retraining, TrustVLM paves the way for safer deployment of VLMs in real-world applications. The code will be available at https://github.com/EPFL-IMOS/TrustVLM.

Modal Decomposition and Identification for a Population of Structures Using Physics-Informed Graph Neural Networks and Transformers

Modal identification is crucial for structural health monitoring and structural control, providing critical insights into structural dynamics and performance. This study presents a novel deep learning framework that integrates graph neural networks (GNNs), transformers, and a physics-informed loss function to achieve modal decomposition and identification across a population of structures. The transformer module decomposes multi-degrees-of-freedom (MDOF) structural dynamic measurements into single-degree-of-freedom (SDOF) modal responses, facilitating the identification of natural frequencies and damping ratios. Concurrently, the GNN captures the structural configurations and identifies mode shapes corresponding to the decomposed SDOF modal responses. The proposed model is trained in a purely physics-informed and unsupervised manner, leveraging modal decomposition theory and the independence of structural modes to guide learning without the need for labeled data. Validation through numerical simulations and laboratory experiments demonstrates its effectiveness in accurately decomposing dynamic responses and identifying modal properties from sparse structural dynamic measurements, regardless of variations in external loads or structural configurations. Comparative analyses against established modal identification techniques and model variations further underscore its superior performance, positioning it as a favorable approach for population-based structural health monitoring.

Grammar-based Ordinary Differential Equation Discovery

The understanding and modeling of complex physical phenomena through dynamical systems has historically driven scientific progress, as it provides the tools for predicting the behavior of different systems under diverse conditions through time. The discovery of dynamical systems has been indispensable in engineering, as it allows for the analysis and prediction of complex behaviors for computational modeling, diagnostics, prognostics, and control of engineered systems. Joining recent efforts that harness the power of symbolic regression in this domain, we propose a novel framework for the end-to-end discovery of ordinary differential equations (ODEs), termed Grammar-based ODE Discovery Engine (GODE). The proposed methodology combines formal grammars with dimensionality reduction and stochastic search for efficiently navigating high-dimensional combinatorial spaces. Grammars allow us to seed domain knowledge and structure for both constraining, as well as, exploring the space of candidate expressions. GODE proves to be more sample- and parameter-efficient than state-of-the-art transformer-based models and to discover more accurate and parsimonious ODE expressions than both genetic programming- and other grammar-based methods for more complex inference tasks, such as the discovery of structural dynamics. Thus, we introduce a tool that could play a catalytic role in dynamics discovery tasks, including modeling, system identification, and monitoring tasks.

Deep Belief Markov Models for POMDP Inference

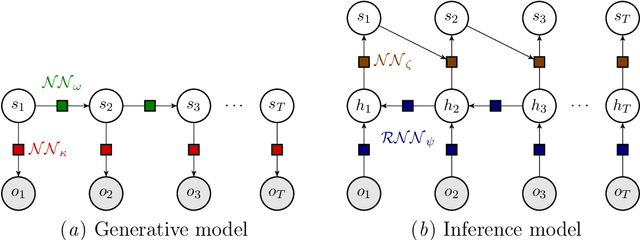
This work introduces a novel deep learning-based architecture, termed the Deep Belief Markov Model (DBMM), which provides efficient, model-formulation agnostic inference in Partially Observable Markov Decision Process (POMDP) problems. The POMDP framework allows for modeling and solving sequential decision-making problems under observation uncertainty. In complex, high-dimensional, partially observable environments, existing methods for inference based on exact computations (e.g., via Bayes' theorem) or sampling algorithms do not scale well. Furthermore, ground truth states may not be available for learning the exact transition dynamics. DBMMs extend deep Markov models into the partially observable decision-making framework and allow efficient belief inference entirely based on available observation data via variational inference methods. By leveraging the potency of neural networks, DBMMs can infer and simulate non-linear relationships in the system dynamics and naturally scale to problems with high dimensionality and discrete or continuous variables. In addition, neural network parameters can be dynamically updated efficiently based on data availability. DBMMs can thus be used to infer a belief variable, thus enabling the derivation of POMDP solutions over the belief space. We evaluate the efficacy of the proposed methodology by evaluating the capability of model-formulation agnostic inference of DBMMs in benchmark problems that include discrete and continuous variables.

Advances in Multimodal Adaptation and Generalization: From Traditional Approaches to Foundation Models

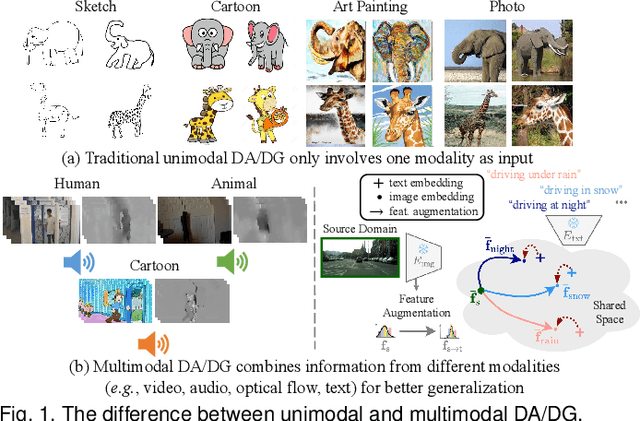
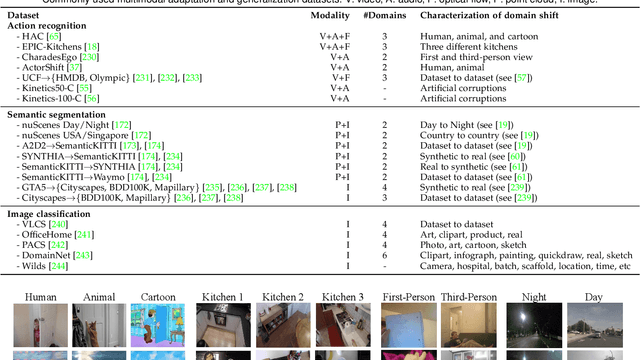
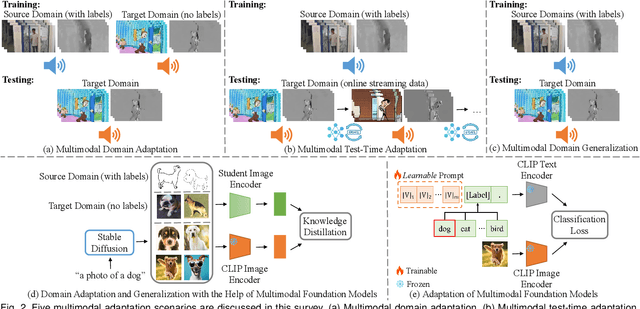
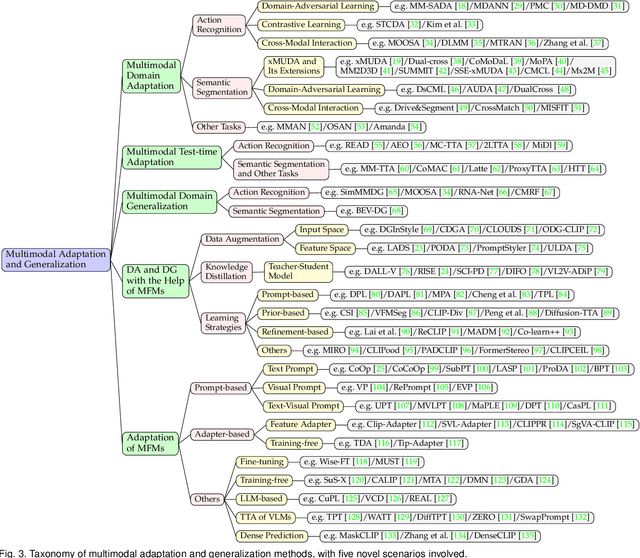
In real-world scenarios, achieving domain adaptation and generalization poses significant challenges, as models must adapt to or generalize across unknown target distributions. Extending these capabilities to unseen multimodal distributions, i.e., multimodal domain adaptation and generalization, is even more challenging due to the distinct characteristics of different modalities. Significant progress has been made over the years, with applications ranging from action recognition to semantic segmentation. Besides, the recent advent of large-scale pre-trained multimodal foundation models, such as CLIP, has inspired works leveraging these models to enhance adaptation and generalization performances or adapting them to downstream tasks. This survey provides the first comprehensive review of recent advances from traditional approaches to foundation models, covering: (1) Multimodal domain adaptation; (2) Multimodal test-time adaptation; (3) Multimodal domain generalization; (4) Domain adaptation and generalization with the help of multimodal foundation models; and (5) Adaptation of multimodal foundation models. For each topic, we formally define the problem and thoroughly review existing methods. Additionally, we analyze relevant datasets and applications, highlighting open challenges and potential future research directions. We maintain an active repository that contains up-to-date literature at https://github.com/donghao51/Awesome-Multimodal-Adaptation.

Graph Transformers for inverse physics: reconstructing flows around arbitrary 2D airfoils

We introduce a Graph Transformer framework that serves as a general inverse physics engine on meshes, demonstrated through the challenging task of reconstructing aerodynamic flow fields from sparse surface measurements. While deep learning has shown promising results in forward physics simulation, inverse problems remain particularly challenging due to their ill-posed nature and the difficulty of propagating information from limited boundary observations. Our approach addresses these challenges by combining the geometric expressiveness of message-passing neural networks with the global reasoning of Transformers, enabling efficient learning of inverse mappings from boundary conditions to complete states. We evaluate this framework on a comprehensive dataset of steady-state RANS simulations around diverse airfoil geometries, where the task is to reconstruct full pressure and velocity fields from surface pressure measurements alone. The architecture achieves high reconstruction accuracy while maintaining fast inference times. We conduct experiments and provide insights into the relative importance of local geometric processing and global attention mechanisms in mesh-based inverse problems. We also find that the framework is robust to reduced sensor coverage. These results suggest that Graph Transformers can serve as effective inverse physics engines across a broader range of applications where complete system states must be reconstructed from limited boundary observations.

Towards Robust Multimodal Open-set Test-time Adaptation via Adaptive Entropy-aware Optimization

Test-time adaptation (TTA) has demonstrated significant potential in addressing distribution shifts between training and testing data. Open-set test-time adaptation (OSTTA) aims to adapt a source pre-trained model online to an unlabeled target domain that contains unknown classes. This task becomes more challenging when multiple modalities are involved. Existing methods have primarily focused on unimodal OSTTA, often filtering out low-confidence samples without addressing the complexities of multimodal data. In this work, we present Adaptive Entropy-aware Optimization (AEO), a novel framework specifically designed to tackle Multimodal Open-set Test-time Adaptation (MM-OSTTA) for the first time. Our analysis shows that the entropy difference between known and unknown samples in the target domain strongly correlates with MM-OSTTA performance. To leverage this, we propose two key components: Unknown-aware Adaptive Entropy Optimization (UAE) and Adaptive Modality Prediction Discrepancy Optimization (AMP). These components enhance the ability of model to distinguish unknown class samples during online adaptation by amplifying the entropy difference between known and unknown samples. To thoroughly evaluate our proposed methods in the MM-OSTTA setting, we establish a new benchmark derived from existing datasets. This benchmark includes two downstream tasks and incorporates five modalities. Extensive experiments across various domain shift situations demonstrate the efficacy and versatility of the AEO framework. Additionally, we highlight the strong performance of AEO in long-term and continual MM-OSTTA settings, both of which are challenging and highly relevant to real-world applications. Our source code is available at https://github.com/donghao51/AEO.