Giacomo Arcieri
Deep Belief Markov Models for POMDP Inference
Mar 17, 2025

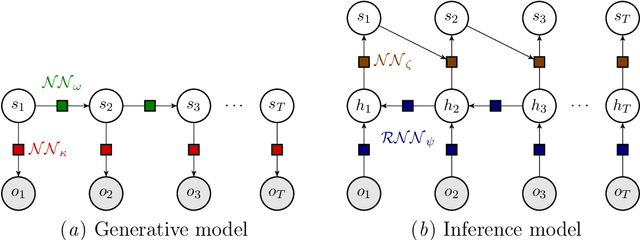

Abstract:This work introduces a novel deep learning-based architecture, termed the Deep Belief Markov Model (DBMM), which provides efficient, model-formulation agnostic inference in Partially Observable Markov Decision Process (POMDP) problems. The POMDP framework allows for modeling and solving sequential decision-making problems under observation uncertainty. In complex, high-dimensional, partially observable environments, existing methods for inference based on exact computations (e.g., via Bayes' theorem) or sampling algorithms do not scale well. Furthermore, ground truth states may not be available for learning the exact transition dynamics. DBMMs extend deep Markov models into the partially observable decision-making framework and allow efficient belief inference entirely based on available observation data via variational inference methods. By leveraging the potency of neural networks, DBMMs can infer and simulate non-linear relationships in the system dynamics and naturally scale to problems with high dimensionality and discrete or continuous variables. In addition, neural network parameters can be dynamically updated efficiently based on data availability. DBMMs can thus be used to infer a belief variable, thus enabling the derivation of POMDP solutions over the belief space. We evaluate the efficacy of the proposed methodology by evaluating the capability of model-formulation agnostic inference of DBMMs in benchmark problems that include discrete and continuous variables.
POMDP inference and robust solution via deep reinforcement learning: An application to railway optimal maintenance
Jul 16, 2023Abstract:Partially Observable Markov Decision Processes (POMDPs) can model complex sequential decision-making problems under stochastic and uncertain environments. A main reason hindering their broad adoption in real-world applications is the lack of availability of a suitable POMDP model or a simulator thereof. Available solution algorithms, such as Reinforcement Learning (RL), require the knowledge of the transition dynamics and the observation generating process, which are often unknown and non-trivial to infer. In this work, we propose a combined framework for inference and robust solution of POMDPs via deep RL. First, all transition and observation model parameters are jointly inferred via Markov Chain Monte Carlo sampling of a hidden Markov model, which is conditioned on actions, in order to recover full posterior distributions from the available data. The POMDP with uncertain parameters is then solved via deep RL techniques with the parameter distributions incorporated into the solution via domain randomization, in order to develop solutions that are robust to model uncertainty. As a further contribution, we compare the use of transformers and long short-term memory networks, which constitute model-free RL solutions, with a model-based/model-free hybrid approach. We apply these methods to the real-world problem of optimal maintenance planning for railway assets.
Bridging POMDPs and Bayesian decision making for robust maintenance planning under model uncertainty: An application to railway systems
Dec 15, 2022Abstract:Structural Health Monitoring (SHM) describes a process for inferring quantifiable metrics of structural condition, which can serve as input to support decisions on the operation and maintenance of infrastructure assets. Given the long lifespan of critical structures, this problem can be cast as a sequential decision making problem over prescribed horizons. Partially Observable Markov Decision Processes (POMDPs) offer a formal framework to solve the underlying optimal planning task. However, two issues can undermine the POMDP solutions. Firstly, the need for a model that can adequately describe the evolution of the structural condition under deterioration or corrective actions and, secondly, the non-trivial task of recovery of the observation process parameters from available monitoring data. Despite these potential challenges, the adopted POMDP models do not typically account for uncertainty on model parameters, leading to solutions which can be unrealistically confident. In this work, we address both key issues. We present a framework to estimate POMDP transition and observation model parameters directly from available data, via Markov Chain Monte Carlo (MCMC) sampling of a Hidden Markov Model (HMM) conditioned on actions. The MCMC inference estimates distributions of the involved model parameters. We then form and solve the POMDP problem by exploiting the inferred distributions, to derive solutions that are robust to model uncertainty. We successfully apply our approach on maintenance planning for railway track assets on the basis of a "fractal value" indicator, which is computed from actual railway monitoring data.
Which Model To Trust: Assessing the Influence of Models on the Performance of Reinforcement Learning Algorithms for Continuous Control Tasks
Oct 25, 2021



Abstract:The need for algorithms able to solve Reinforcement Learning (RL) problems with few trials has motivated the advent of model-based RL methods. The reported performance of model-based algorithms has dramatically increased within recent years. However, it is not clear how much of the recent progress is due to improved algorithms or due to improved models. While different modeling options are available to choose from when applying a model-based approach, the distinguishing traits and particular strengths of different models are not clear. The main contribution of this work lies precisely in assessing the model influence on the performance of RL algorithms. A set of commonly adopted models is established for the purpose of model comparison. These include Neural Networks (NNs), ensembles of NNs, two different approximations of Bayesian NNs (BNNs), that is, the Concrete Dropout NN and the Anchored Ensembling, and Gaussian Processes (GPs). The model comparison is evaluated on a suite of continuous control benchmarking tasks. Our results reveal that significant differences in model performance do exist. The Concrete Dropout NN reports persistently superior performance. We summarize these differences for the benefit of the modeler and suggest that the model choice is tailored to the standards required by each specific application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge