Deep Belief Markov Models for POMDP Inference

This work introduces a novel deep learning-based architecture, termed the Deep Belief Markov Model (DBMM), which provides efficient, model-formulation agnostic inference in Partially Observable Markov Decision Process (POMDP) problems. The POMDP framework allows for modeling and solving sequential decision-making problems under observation uncertainty. In complex, high-dimensional, partially observable environments, existing methods for inference based on exact computations (e.g., via Bayes' theorem) or sampling algorithms do not scale well. Furthermore, ground truth states may not be available for learning the exact transition dynamics. DBMMs extend deep Markov models into the partially observable decision-making framework and allow efficient belief inference entirely based on available observation data via variational inference methods. By leveraging the potency of neural networks, DBMMs can infer and simulate non-linear relationships in the system dynamics and naturally scale to problems with high dimensionality and discrete or continuous variables. In addition, neural network parameters can be dynamically updated efficiently based on data availability. DBMMs can thus be used to infer a belief variable, thus enabling the derivation of POMDP solutions over the belief space. We evaluate the efficacy of the proposed methodology by evaluating the capability of model-formulation agnostic inference of DBMMs in benchmark problems that include discrete and continuous variables.

POMDP inference and robust solution via deep reinforcement learning: An application to railway optimal maintenance

Partially Observable Markov Decision Processes (POMDPs) can model complex sequential decision-making problems under stochastic and uncertain environments. A main reason hindering their broad adoption in real-world applications is the lack of availability of a suitable POMDP model or a simulator thereof. Available solution algorithms, such as Reinforcement Learning (RL), require the knowledge of the transition dynamics and the observation generating process, which are often unknown and non-trivial to infer. In this work, we propose a combined framework for inference and robust solution of POMDPs via deep RL. First, all transition and observation model parameters are jointly inferred via Markov Chain Monte Carlo sampling of a hidden Markov model, which is conditioned on actions, in order to recover full posterior distributions from the available data. The POMDP with uncertain parameters is then solved via deep RL techniques with the parameter distributions incorporated into the solution via domain randomization, in order to develop solutions that are robust to model uncertainty. As a further contribution, we compare the use of transformers and long short-term memory networks, which constitute model-free RL solutions, with a model-based/model-free hybrid approach. We apply these methods to the real-world problem of optimal maintenance planning for railway assets.

Bridging POMDPs and Bayesian decision making for robust maintenance planning under model uncertainty: An application to railway systems

Structural Health Monitoring (SHM) describes a process for inferring quantifiable metrics of structural condition, which can serve as input to support decisions on the operation and maintenance of infrastructure assets. Given the long lifespan of critical structures, this problem can be cast as a sequential decision making problem over prescribed horizons. Partially Observable Markov Decision Processes (POMDPs) offer a formal framework to solve the underlying optimal planning task. However, two issues can undermine the POMDP solutions. Firstly, the need for a model that can adequately describe the evolution of the structural condition under deterioration or corrective actions and, secondly, the non-trivial task of recovery of the observation process parameters from available monitoring data. Despite these potential challenges, the adopted POMDP models do not typically account for uncertainty on model parameters, leading to solutions which can be unrealistically confident. In this work, we address both key issues. We present a framework to estimate POMDP transition and observation model parameters directly from available data, via Markov Chain Monte Carlo (MCMC) sampling of a Hidden Markov Model (HMM) conditioned on actions. The MCMC inference estimates distributions of the involved model parameters. We then form and solve the POMDP problem by exploiting the inferred distributions, to derive solutions that are robust to model uncertainty. We successfully apply our approach on maintenance planning for railway track assets on the basis of a "fractal value" indicator, which is computed from actual railway monitoring data.

Inference and dynamic decision-making for deteriorating systems with probabilistic dependencies through Bayesian networks and deep reinforcement learning

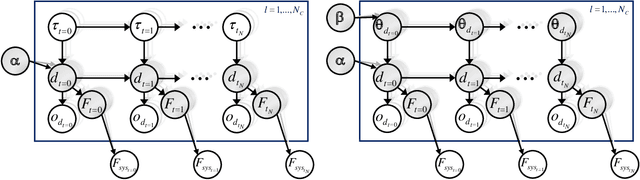
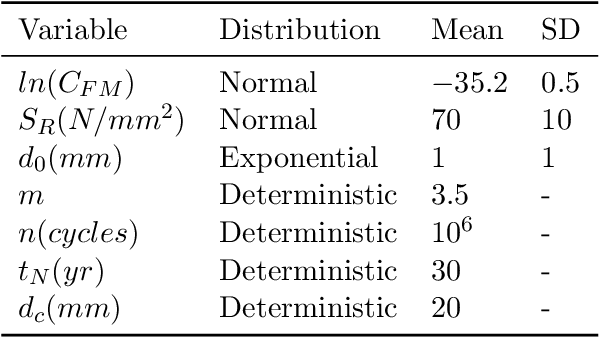
In the context of modern environmental and societal concerns, there is an increasing demand for methods able to identify management strategies for civil engineering systems, minimizing structural failure risks while optimally planning inspection and maintenance (I&M) processes. Most available methods simplify the I&M decision problem to the component level due to the computational complexity associated with global optimization methodologies under joint system-level state descriptions. In this paper, we propose an efficient algorithmic framework for inference and decision-making under uncertainty for engineering systems exposed to deteriorating environments, providing optimal management strategies directly at the system level. In our approach, the decision problem is formulated as a factored partially observable Markov decision process, whose dynamics are encoded in Bayesian network conditional structures. The methodology can handle environments under equal or general, unequal deterioration correlations among components, through Gaussian hierarchical structures and dynamic Bayesian networks. In terms of policy optimization, we adopt a deep decentralized multi-agent actor-critic (DDMAC) reinforcement learning approach, in which the policies are approximated by actor neural networks guided by a critic network. By including deterioration dependence in the simulated environment, and by formulating the cost model at the system level, DDMAC policies intrinsically consider the underlying system-effects. This is demonstrated through numerical experiments conducted for both a 9-out-of-10 system and a steel frame under fatigue deterioration. Results demonstrate that DDMAC policies offer substantial benefits when compared to state-of-the-art heuristic approaches. The inherent consideration of system-effects by DDMAC strategies is also interpreted based on the learned policies.