Safety integrity framework for automated driving

This paper describes the comprehensive safety framework that underpinned the development, release process, and regulatory approval of BMW's first SAE Level 3 Automated Driving System. The framework combines established qualitative and quantitative methods from the fields of Systems Engineering, Engineering Risk Analysis, Bayesian Data Analysis, Design of Experiments, and Statistical Learning in a novel manner. The approach systematically minimizes the risks associated with hardware and software faults, performance limitations, and insufficient specifications to an acceptable level that achieves a Positive Risk Balance. At the core of the framework is the systematic identification and quantification of uncertainties associated with hazard scenarios and the redundantly designed system based on designed experiments, field data, and expert knowledge. The residual risk of the system is then estimated through Stochastic Simulation and evaluated by Sensitivity Analysis. By integrating these advanced analytical techniques into the V-Model, the framework fulfills, unifies, and complements existing automotive safety standards. It therefore provides a comprehensive, rigorous, and transparent safety assurance process for the development and deployment of Automated Driving Systems.

Deep Belief Markov Models for POMDP Inference

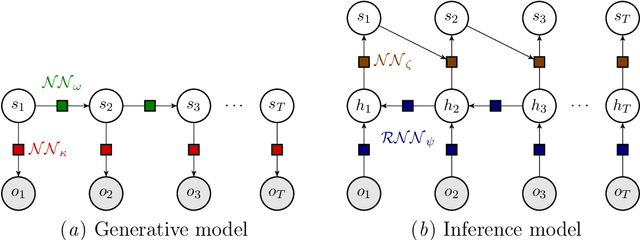
This work introduces a novel deep learning-based architecture, termed the Deep Belief Markov Model (DBMM), which provides efficient, model-formulation agnostic inference in Partially Observable Markov Decision Process (POMDP) problems. The POMDP framework allows for modeling and solving sequential decision-making problems under observation uncertainty. In complex, high-dimensional, partially observable environments, existing methods for inference based on exact computations (e.g., via Bayes' theorem) or sampling algorithms do not scale well. Furthermore, ground truth states may not be available for learning the exact transition dynamics. DBMMs extend deep Markov models into the partially observable decision-making framework and allow efficient belief inference entirely based on available observation data via variational inference methods. By leveraging the potency of neural networks, DBMMs can infer and simulate non-linear relationships in the system dynamics and naturally scale to problems with high dimensionality and discrete or continuous variables. In addition, neural network parameters can be dynamically updated efficiently based on data availability. DBMMs can thus be used to infer a belief variable, thus enabling the derivation of POMDP solutions over the belief space. We evaluate the efficacy of the proposed methodology by evaluating the capability of model-formulation agnostic inference of DBMMs in benchmark problems that include discrete and continuous variables.

Convex Is Back: Solving Belief MDPs With Convexity-Informed Deep Reinforcement Learning

We present a novel method for Deep Reinforcement Learning (DRL), incorporating the convex property of the value function over the belief space in Partially Observable Markov Decision Processes (POMDPs). We introduce hard- and soft-enforced convexity as two different approaches, and compare their performance against standard DRL on two well-known POMDP environments, namely the Tiger and FieldVisionRockSample problems. Our findings show that including the convexity feature can substantially increase performance of the agents, as well as increase robustness over the hyperparameter space, especially when testing on out-of-distribution domains. The source code for this work can be found at https://github.com/Dakout/Convex_DRL.

An investigation of belief-free DRL and MCTS for inspection and maintenance planning

We propose a novel Deep Reinforcement Learning (DRL) architecture for sequential decision processes under uncertainty, as encountered in inspection and maintenance (I&M) planning. Unlike other DRL algorithms for (I&M) planning, the proposed +RQN architecture dispenses with computing the belief state and directly handles erroneous observations instead. We apply the algorithm to a basic I&M planning problem for a one-component system subject to deterioration. In addition, we investigate the performance of Monte Carlo tree search for the I&M problem and compare it to the +RQN. The comparison includes a statistical analysis of the two methods' resulting policies, as well as their visualization in the belief space.

POMDP inference and robust solution via deep reinforcement learning: An application to railway optimal maintenance

Partially Observable Markov Decision Processes (POMDPs) can model complex sequential decision-making problems under stochastic and uncertain environments. A main reason hindering their broad adoption in real-world applications is the lack of availability of a suitable POMDP model or a simulator thereof. Available solution algorithms, such as Reinforcement Learning (RL), require the knowledge of the transition dynamics and the observation generating process, which are often unknown and non-trivial to infer. In this work, we propose a combined framework for inference and robust solution of POMDPs via deep RL. First, all transition and observation model parameters are jointly inferred via Markov Chain Monte Carlo sampling of a hidden Markov model, which is conditioned on actions, in order to recover full posterior distributions from the available data. The POMDP with uncertain parameters is then solved via deep RL techniques with the parameter distributions incorporated into the solution via domain randomization, in order to develop solutions that are robust to model uncertainty. As a further contribution, we compare the use of transformers and long short-term memory networks, which constitute model-free RL solutions, with a model-based/model-free hybrid approach. We apply these methods to the real-world problem of optimal maintenance planning for railway assets.

Bridging POMDPs and Bayesian decision making for robust maintenance planning under model uncertainty: An application to railway systems

Structural Health Monitoring (SHM) describes a process for inferring quantifiable metrics of structural condition, which can serve as input to support decisions on the operation and maintenance of infrastructure assets. Given the long lifespan of critical structures, this problem can be cast as a sequential decision making problem over prescribed horizons. Partially Observable Markov Decision Processes (POMDPs) offer a formal framework to solve the underlying optimal planning task. However, two issues can undermine the POMDP solutions. Firstly, the need for a model that can adequately describe the evolution of the structural condition under deterioration or corrective actions and, secondly, the non-trivial task of recovery of the observation process parameters from available monitoring data. Despite these potential challenges, the adopted POMDP models do not typically account for uncertainty on model parameters, leading to solutions which can be unrealistically confident. In this work, we address both key issues. We present a framework to estimate POMDP transition and observation model parameters directly from available data, via Markov Chain Monte Carlo (MCMC) sampling of a Hidden Markov Model (HMM) conditioned on actions. The MCMC inference estimates distributions of the involved model parameters. We then form and solve the POMDP problem by exploiting the inferred distributions, to derive solutions that are robust to model uncertainty. We successfully apply our approach on maintenance planning for railway track assets on the basis of a "fractal value" indicator, which is computed from actual railway monitoring data.

Sparse Polynomial Chaos expansions using Variational Relevance Vector Machines

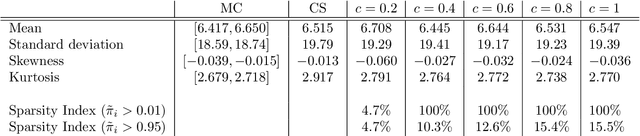
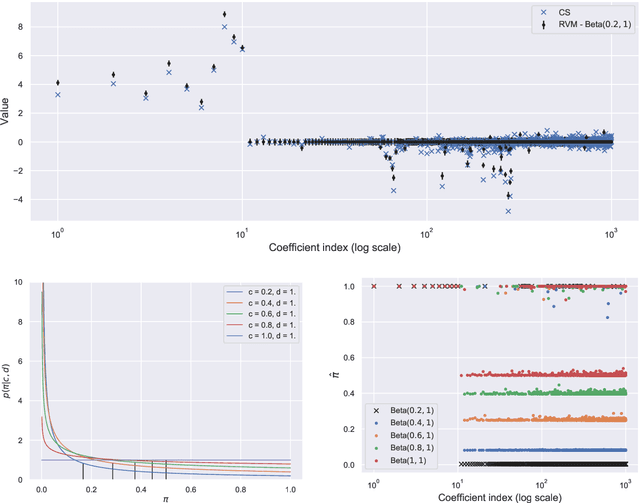
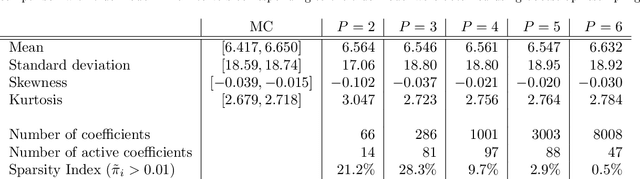
The challenges for non-intrusive methods for Polynomial Chaos modeling lie in the computational efficiency and accuracy under a limited number of model simulations. These challenges can be addressed by enforcing sparsity in the series representation through retaining only the most important basis terms. In this work, we present a novel sparse Bayesian learning technique for obtaining sparse Polynomial Chaos expansions which is based on a Relevance Vector Machine model and is trained using Variational Inference. The methodology shows great potential in high-dimensional data-driven settings using relatively few data points and achieves user-controlled sparse levels that are comparable to other methods such as compressive sensing. The proposed approach is illustrated on two numerical examples, a synthetic response function that is explored for validation purposes and a low-carbon steel plate with random Young's modulus and random loading, which is modeled by stochastic finite element with 38 input random variables.

Bayesian Network Enhanced with Structural Reliability Methods: Methodology

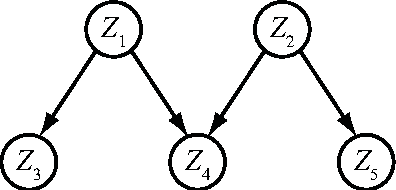
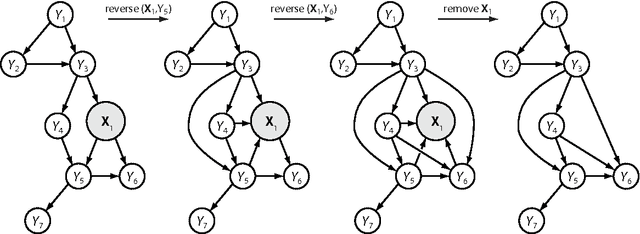
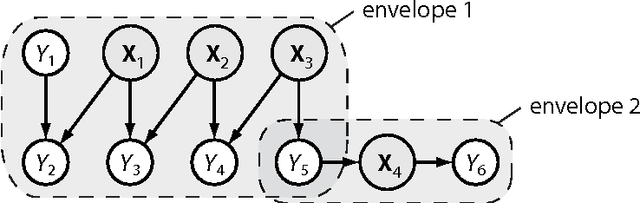
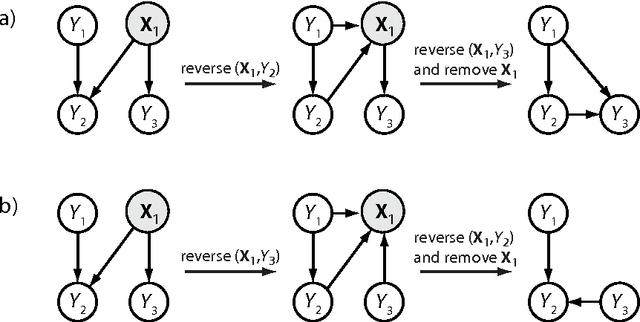
We combine Bayesian networks (BNs) and structural reliability methods (SRMs) to create a new computational framework, termed enhanced Bayesian network (eBN), for reliability and risk analysis of engineering structures and infrastructure. BNs are efficient in representing and evaluating complex probabilistic dependence structures, as present in infrastructure and structural systems, and they facilitate Bayesian updating of the model when new information becomes available. On the other hand, SRMs enable accurate assessment of probabilities of rare events represented by computationally demanding, physically-based models. By combining the two methods, the eBN framework provides a unified and powerful tool for efficiently computing probabilities of rare events in complex structural and infrastructure systems in which information evolves in time. Strategies for modeling and efficiently analyzing the eBN are described by way of several conceptual examples. The companion paper applies the eBN methodology to example structural and infrastructure systems.

Reliability updating with equality information

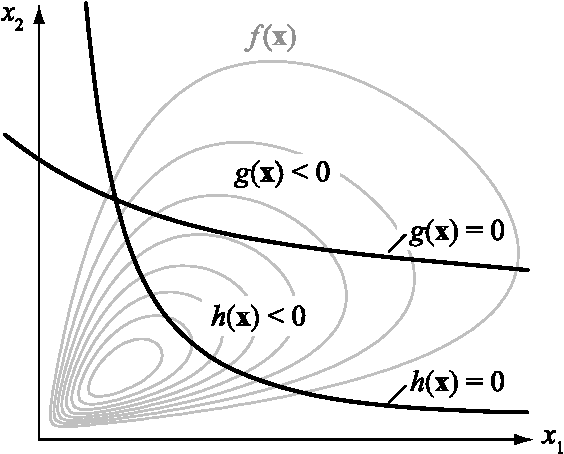
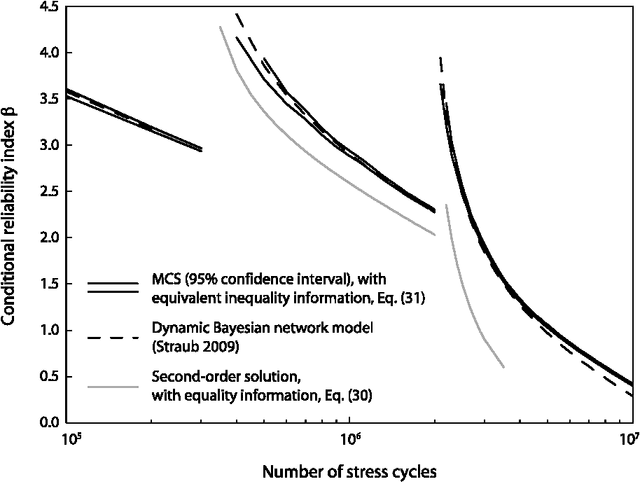
In many instances, information on engineering systems can be obtained through measurements, monitoring or direct observations of system performances and can be used to update the system reliability estimate. In structural reliability analysis, such information is expressed either by inequalities (e.g. for the observation that no defect is present) or by equalities (e.g. for quantitative measurements of system characteristics). When information Z is of the equality type, the a-priori probability of Z is zero and most structural reliability methods (SRM) are not directly applicable to the computation of the updated reliability. Hitherto, the computation of the reliability of engineering systems conditional on equality information was performed through first- and second order approximations. In this paper, it is shown how equality information can be transformed into inequality information, which enables reliability updating by solving a standard structural system reliability problem. This approach enables the use of any SRM, including those based on simulation, for reliability updating with equality information. It is demonstrated on three numerical examples, including an application to fatigue reliability.