Hierarchical Large Scale Multirobot Path (Re)Planning

We consider a large-scale multi-robot path planning problem in a cluttered environment. Our approach achieves real-time replanning by dividing the workspace into cells and utilizing a hierarchical planner. Specifically, multi-commodity flow-based high-level planners route robots through the cells to reduce congestion, while an anytime low-level planner computes collision-free paths for robots within each cell in parallel. Despite resulting in longer paths compared to the baseline multi-agent pathfinding algorithm, our method produces a solution with significant improvement in computation time. Specifically, we show empirical results of a 500-times speedup in computation time compared to the baseline multi-agent pathfinding approach on the environments we study. We account for the robot's embodiment and support non-stop execution when replanning continuously. We demonstrate the real-time performance of our algorithm with up to 142 robots in simulation, and a representative 32 physical Crazyflie nano-quadrotor experiment.

MARLAS: Multi Agent Reinforcement Learning for cooperated Adaptive Sampling

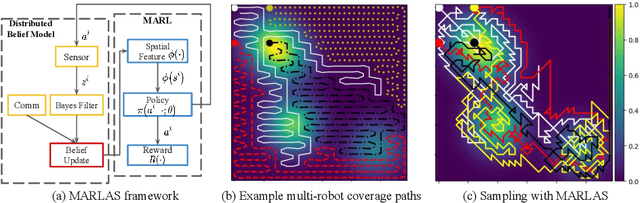
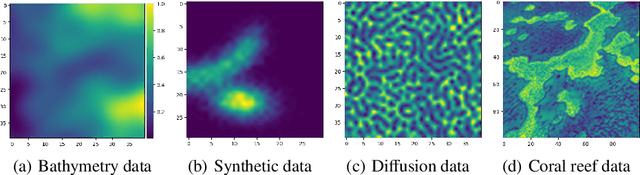
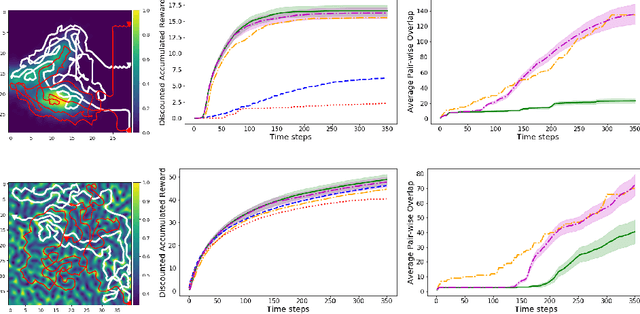
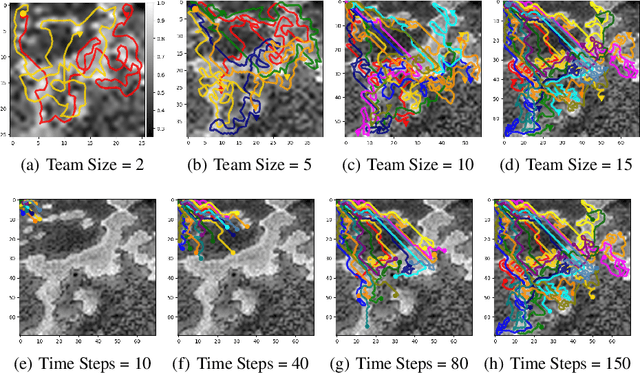
The multi-robot adaptive sampling problem aims at finding trajectories for a team of robots to efficiently sample the phenomenon of interest within a given endurance budget of the robots. In this paper, we propose a robust and scalable approach using decentralized Multi-Agent Reinforcement Learning for cooperated Adaptive Sampling (MARLAS) of quasi-static environmental processes. Given a prior on the field being sampled, the proposed method learns decentralized policies for a team of robots to sample high-utility regions within a fixed budget. The multi-robot adaptive sampling problem requires the robots to coordinate with each other to avoid overlapping sampling trajectories. Therefore, we encode the estimates of neighbor positions and intermittent communication between robots into the learning process. We evaluated MARLAS over multiple performance metrics and found it to outperform other baseline multi-robot sampling techniques. We further demonstrate robustness to communication failures and scalability with both the size of the robot team and the size of the region being sampled. The experimental evaluations are conducted both in simulations on real data and in real robot experiments on demo environmental setup.

Learning to Swarm with Knowledge-Based Neural Ordinary Differential Equations

Understanding single-agent dynamics from collective behaviors in natural swarms is crucial for informing robot controller designs in artificial swarms and multiagent robotic systems. However, the complexity in agent-to-agent interactions and the decentralized nature of most swarms pose a significant challenge to the extraction of single-robot control laws from global behavior. In this work, we consider the important task of learning decentralized single-robot controllers based solely on the state observations of a swarm's trajectory. We present a general framework by adopting knowledge-based neural ordinary differential equations (KNODE) -- a hybrid machine learning method capable of combining artificial neural networks with known agent dynamics. Our approach distinguishes itself from most prior works in that we do not require action data for learning. We apply our framework to two different flocking swarms in 2D and 3D respectively, and demonstrate efficient training by leveraging the graphical structure of the swarms' information network. We further show that the learnt single-robot controllers can not only reproduce flocking behavior in the original swarm but also scale to swarms with more robots.

Linear Multiple Low-Rank Kernel Based Stationary Gaussian Processes Regression for Time Series

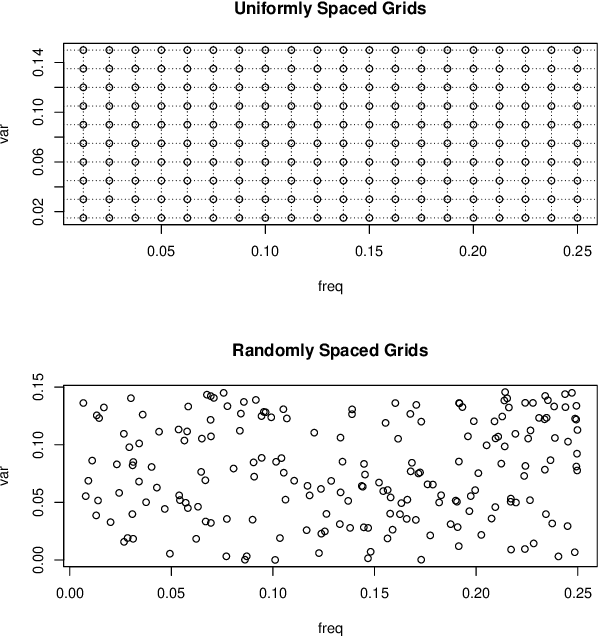
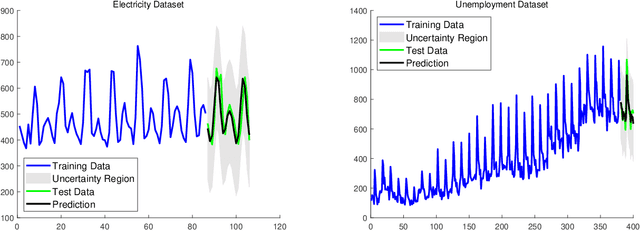
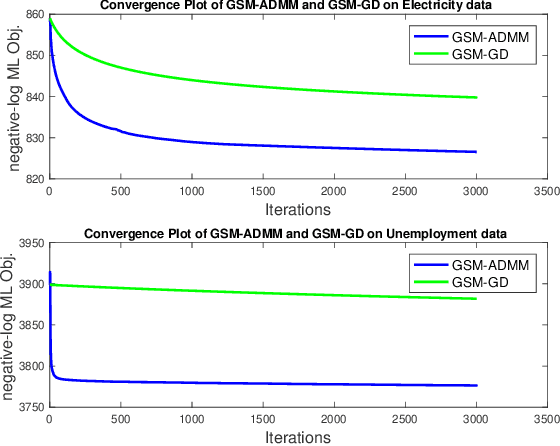
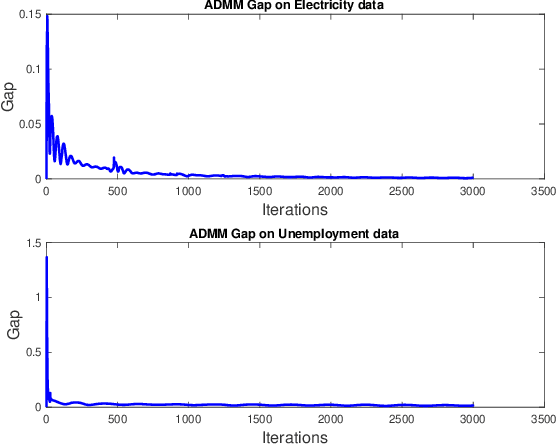
Gaussian processes (GP) for machine learning have been studied systematically over the past two decades and they are by now widely used in a number of diverse applications. However, GP kernel design and the associated hyper-parameter optimization are still hard and to a large extend open problems. In this paper, we consider the task of GP regression for time series modeling and analysis. The underlying stationary kernel can be approximated arbitrarily close by a new proposed grid spectral mixture (GSM) kernel, which turns out to be a linear combination of low-rank sub-kernels. In the case where a large number of the sub-kernels are used, either the Nystr\"{o}m or the random Fourier feature approximations can be adopted to deal efficiently with the computational demands. The unknown GP hyper-parameters consist of the non-negative weights of all sub-kernels as well as the noise variance; their estimation is performed via the maximum-likelihood (ML) estimation framework. Two efficient numerical optimization methods for solving the unknown hyper-parameters are derived, including a sequential majorization-minimization (MM) method and a non-linearly constrained alternating direction of multiplier method (ADMM). The MM matches perfectly with the proven low-rank property of the proposed GSM sub-kernels and turns out to be a part of efficiency, stable, and efficient solver, while the ADMM has the potential to generate better local minimum in terms of the test MSE. Experimental results, based on various classic time series data sets, corroborate that the proposed GSM kernel-based GP regression model outperforms several salient competitors of similar kind in terms of prediction mean-squared-error and numerical stability.