Amplitude-Domain Reflection Modulation for Active RIS-Assisted Wireless Communications

In this paper, we propose a novel active reconfigurable intelligent surface (RIS)-assisted amplitude-domain reflection modulation (ADRM) transmission scheme, termed as ARIS-ADRM. This innovative approach leverages the additional degree of freedom (DoF) provided by the amplitude domain of the active RIS to perform index modulation (IM), thereby enhancing spectral efficiency (SE) without increasing the costs associated with additional radio frequency (RF) chains. Specifically, the ARIS-ADRM scheme transmits information bits through both the modulation symbol and the index of active RIS amplitude allocation patterns (AAPs). To evaluate the performance of the proposed ARIS-ADRM scheme, we provide an achievable rate analysis and derive a closed-form expression for the upper bound on the average bit error probability (ABEP). Furthermore, we formulate an optimization problem to construct the AAP codebook, aiming to minimize the ABEP. Simulation results demonstrate that the proposed scheme significantly improves error performance under the same SE conditions compared to its benchmarks. This improvement is due to its ability to flexibly adapt the transmission rate by fully exploiting the amplitude domain DoF provided by the active RIS.

Beyond FVD: Enhanced Evaluation Metrics for Video Generation Quality

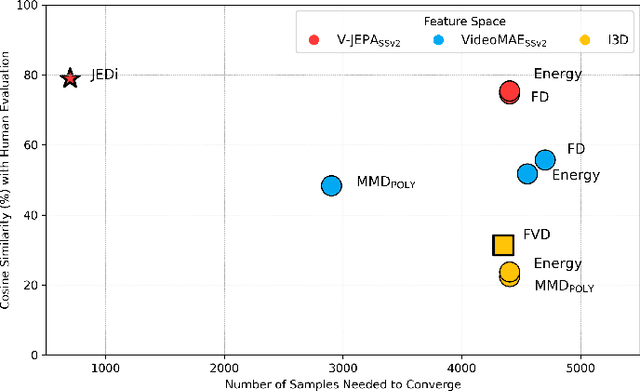
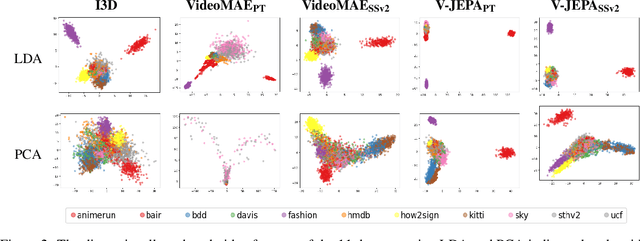
The Fr\'echet Video Distance (FVD) is a widely adopted metric for evaluating video generation distribution quality. However, its effectiveness relies on critical assumptions. Our analysis reveals three significant limitations: (1) the non-Gaussianity of the Inflated 3D Convnet (I3D) feature space; (2) the insensitivity of I3D features to temporal distortions; (3) the impractical sample sizes required for reliable estimation. These findings undermine FVD's reliability and show that FVD falls short as a standalone metric for video generation evaluation. After extensive analysis of a wide range of metrics and backbone architectures, we propose JEDi, the JEPA Embedding Distance, based on features derived from a Joint Embedding Predictive Architecture, measured using Maximum Mean Discrepancy with polynomial kernel. Our experiments on multiple open-source datasets show clear evidence that it is a superior alternative to the widely used FVD metric, requiring only 16% of the samples to reach its steady value, while increasing alignment with human evaluation by 34%, on average.

Linear Multiple Low-Rank Kernel Based Stationary Gaussian Processes Regression for Time Series

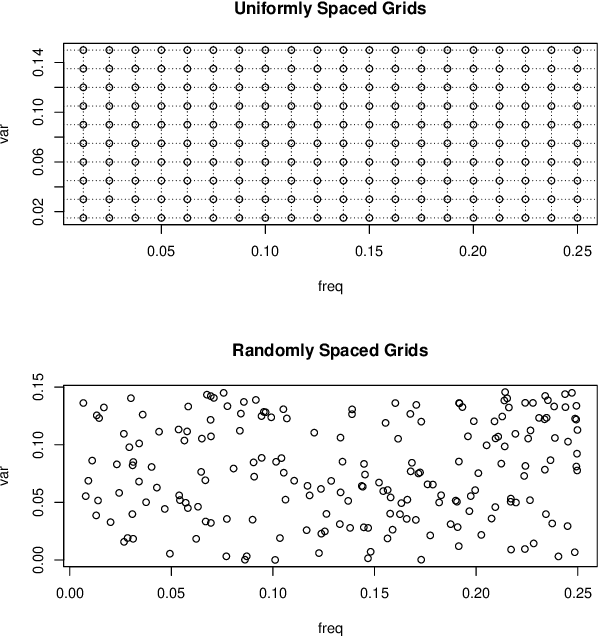
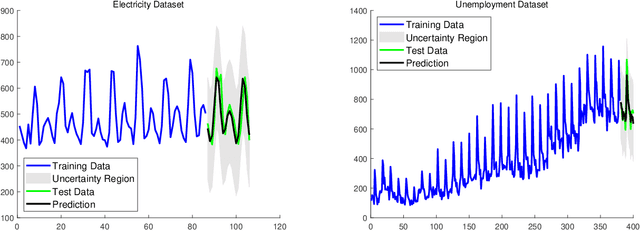
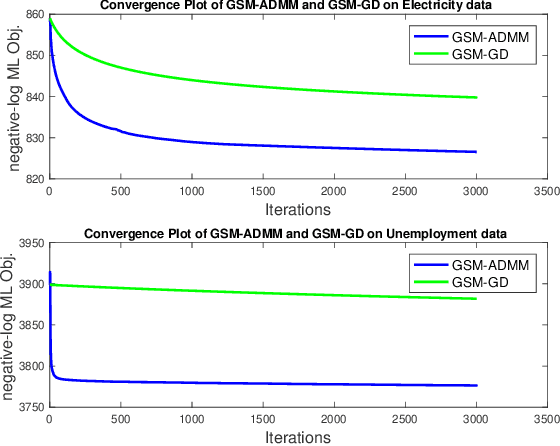
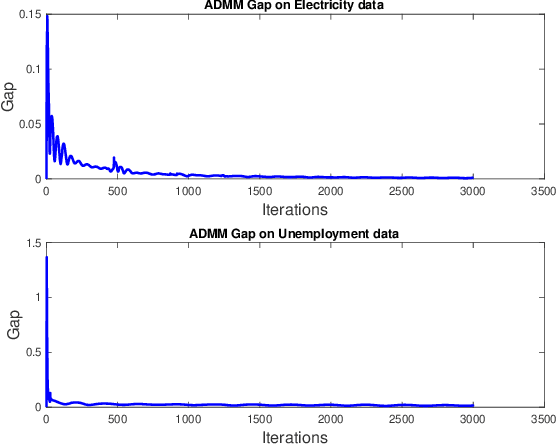
Gaussian processes (GP) for machine learning have been studied systematically over the past two decades and they are by now widely used in a number of diverse applications. However, GP kernel design and the associated hyper-parameter optimization are still hard and to a large extend open problems. In this paper, we consider the task of GP regression for time series modeling and analysis. The underlying stationary kernel can be approximated arbitrarily close by a new proposed grid spectral mixture (GSM) kernel, which turns out to be a linear combination of low-rank sub-kernels. In the case where a large number of the sub-kernels are used, either the Nystr\"{o}m or the random Fourier feature approximations can be adopted to deal efficiently with the computational demands. The unknown GP hyper-parameters consist of the non-negative weights of all sub-kernels as well as the noise variance; their estimation is performed via the maximum-likelihood (ML) estimation framework. Two efficient numerical optimization methods for solving the unknown hyper-parameters are derived, including a sequential majorization-minimization (MM) method and a non-linearly constrained alternating direction of multiplier method (ADMM). The MM matches perfectly with the proven low-rank property of the proposed GSM sub-kernels and turns out to be a part of efficiency, stable, and efficient solver, while the ADMM has the potential to generate better local minimum in terms of the test MSE. Experimental results, based on various classic time series data sets, corroborate that the proposed GSM kernel-based GP regression model outperforms several salient competitors of similar kind in terms of prediction mean-squared-error and numerical stability.