Exploring the Dynamics of Lotka-Volterra Systems: Efficiency, Extinction Order, and Predictive Machine Learning

For years, a main focus of ecological research has been to better understand the complex dynamical interactions between species which comprise food webs. Using the connectance properties of a widely explored synthetic food web called the cascade model, we explore the behavior of dynamics on Lotka-Volterra ecological systems. We show how trophic efficiency, a staple assumption in mathematical ecology, produces systems which are not persistent. With clustering analysis we show how straightforward inequalities of the summed values of the birth, death, self-regulation and interaction strengths provide insight into which food webs are more enduring or stable. Through these simplified summed values, we develop a random forest model and a neural network model, both of which are able to predict the number of extinctions that would occur without the need to simulate the dynamics. To conclude, we highlight the variable that plays the dominant role in determining the order in which species go extinct.

Learning Nonlinear Dynamics and Chaos: A Universal Framework for Knowledge-Based System Identification and Prediction

We present a universal framework for learning the behavior of dynamical systems from observations. We formulate the learning task as a constrained optimization problem which can be efficiently solved with the adjoint sensitivity method. Our scheme is flexible with regards to the choice of model, and existing knowledge can be readily incorporated for hybrid learning. We demonstrate the effectiveness of our scheme by learning a variety of systems including a stiff Van der Pol oscillator, a chaotic Lorenz system, and the Kuramoto-Sivashinsky equation. We also include examples of hybrid learning and learning from noisy observations.

Bridging the Gap: Machine Learning to Resolve Improperly Modeled Dynamics

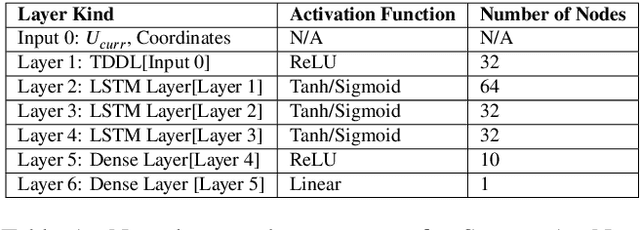
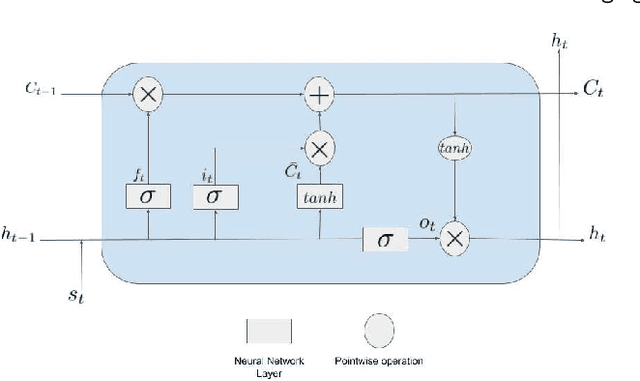
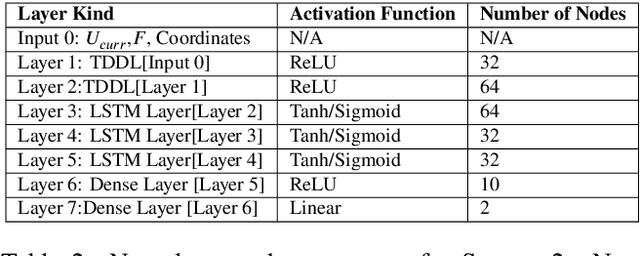
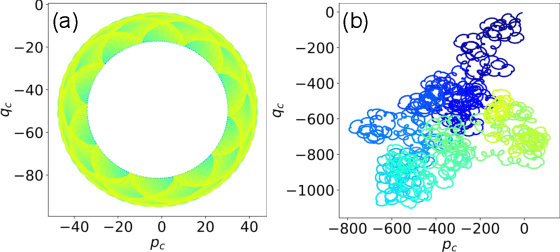
We present a data-driven modeling strategy to overcome improperly modeled dynamics for systems exhibiting complex spatio-temporal behaviors. We propose a Deep Learning framework to resolve the differences between the true dynamics of the system and the dynamics given by a model of the system that is either inaccurately or inadequately described. Our machine learning strategy leverages data generated from the improper system model and observational data from the actual system to create a neural network to model the dynamics of the actual system. We evaluate the proposed framework using numerical solutions obtained from three increasingly complex dynamical systems. Our results show that our system is capable of learning a data-driven model that provides accurate estimates of the system states both in previously unobserved regions as well as for future states. Our results show the power of state-of-the-art machine learning frameworks in estimating an accurate prior of the system's true dynamics that can be used for prediction up to a finite horizon.