Posterior Variance Analysis of Gaussian Processes with Application to Average Learning Curves
Paper and Code
Jun 04, 2019
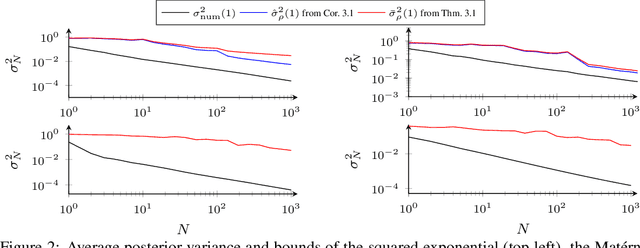
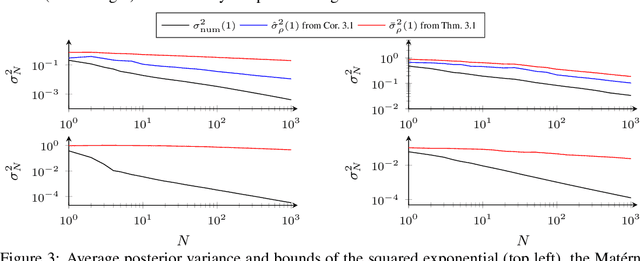
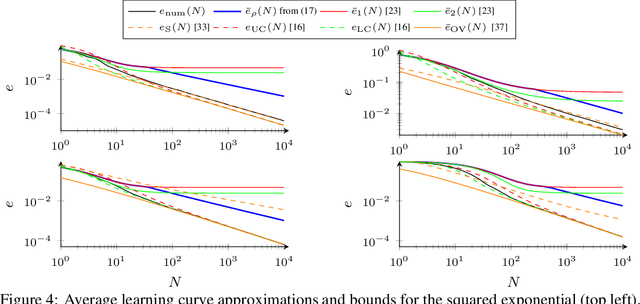
The posterior variance of Gaussian processes is a valuable measure of the learning error which is exploited in various applications such as safe reinforcement learning and control design. However, suitable analysis of the posterior variance which captures its behavior for finite and infinite number of training data is missing. This paper derives a novel bound for the posterior variance function which requires only local information because it depends only on the number of training samples in the proximity of a considered test point. Furthermore, we prove sufficient conditions which ensure the convergence of the posterior variance to zero. Finally, we demonstrate that the extension of our bound to an average learning bound outperforms existing approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge