Towards Efficient Risk-Sensitive Policy Gradient: An Iteration Complexity Analysis

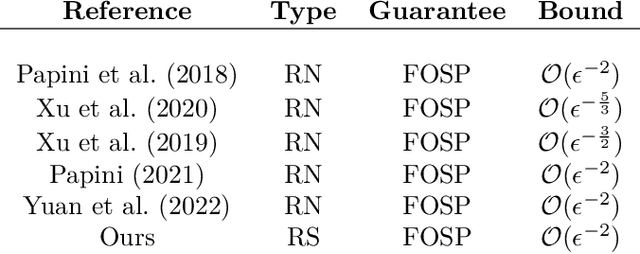
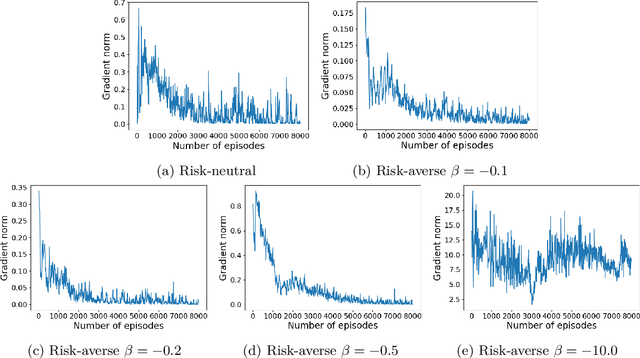
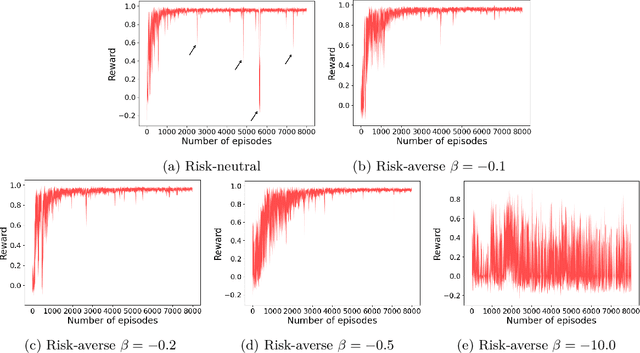
Reinforcement Learning (RL) has shown exceptional performance across various applications, enabling autonomous agents to learn optimal policies through interaction with their environments. However, traditional RL frameworks often face challenges in terms of iteration complexity and robustness. Risk-sensitive RL, which balances expected return and risk, has been explored for its potential to yield probabilistically robust policies, yet its iteration complexity analysis remains underexplored. In this study, we conduct a thorough iteration complexity analysis for the risk-sensitive policy gradient method, focusing on the REINFORCE algorithm and employing the exponential utility function. We obtain an iteration complexity of $\mathcal{O}(\epsilon^{-2})$ to reach an $\epsilon$-approximate first-order stationary point (FOSP). We investigate whether risk-sensitive algorithms can achieve better iteration complexity compared to their risk-neutral counterparts. Our theoretical analysis demonstrates that risk-sensitive REINFORCE can have a reduced number of iterations required for convergence. This leads to improved iteration complexity, as employing the exponential utility does not entail additional computation per iteration. We characterize the conditions under which risk-sensitive algorithms can achieve better iteration complexity. Our simulation results also validate that risk-averse cases can converge and stabilize more quickly after approximately half of the episodes compared to their risk-neutral counterparts.