Optimal Transport for Correctional Learning

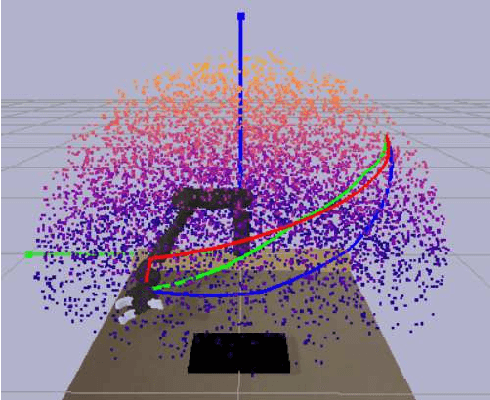
The contribution of this paper is a generalized formulation of correctional learning using optimal transport, which is about how to optimally transport one mass distribution to another. Correctional learning is a framework developed to enhance the accuracy of parameter estimation processes by means of a teacher-student approach. In this framework, an expert agent, referred to as the teacher, modifies the data used by a learning agent, known as the student, to improve its estimation process. The objective of the teacher is to alter the data such that the student's estimation error is minimized, subject to a fixed intervention budget. Compared to existing formulations of correctional learning, our novel optimal transport approach provides several benefits. It allows for the estimation of more complex characteristics as well as the consideration of multiple intervention policies for the teacher. We evaluate our approach on two theoretical examples, and on a human-robot interaction application in which the teacher's role is to improve the robots performance in an inverse reinforcement learning setting.

A teacher-student framework for online correctional learning

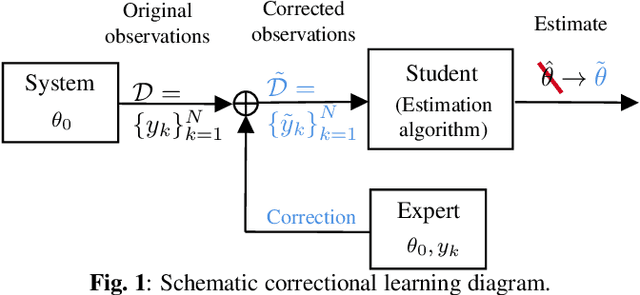
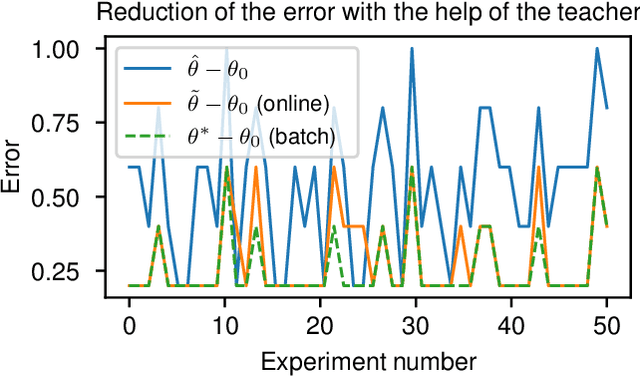
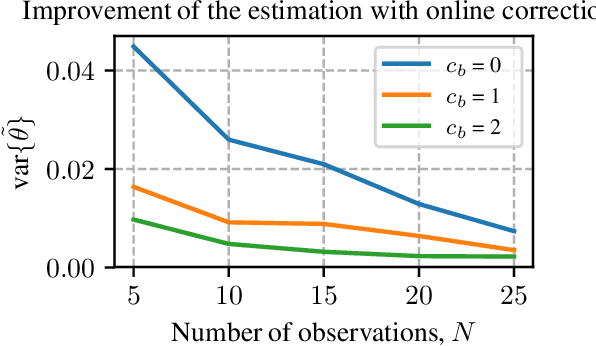
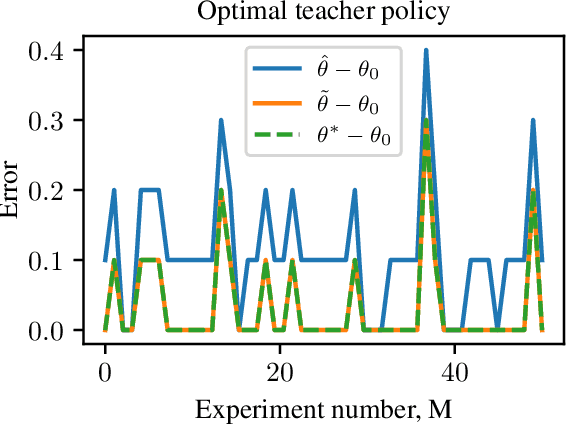
A classical learning setting is one in which a student collects data, or observations, about a system, and estimates a certain quantity of interest about it. Correctional learning is a type of cooperative teacher-student framework where a teacher, who has knowledge about the system, has the possibility to observe and alter (correct) the observations received by the student in order to improve its estimation. In this paper, we show that the variance of the estimate of the student is reduced with the help of the teacher. We further formulate the online problem - where the teacher has to decide at each time instant whether or not to change the observations - as a Markov decision process, from which the optimal policy is derived using dynamic programming. We validate the framework in numerical experiments, and compare the optimal online policy with the one from the batch setting.

On Training and Evaluation of Neural Network Approaches for Model Predictive Control

The contribution of this paper is a framework for training and evaluation of Model Predictive Control (MPC) implemented using constrained neural networks. Recent studies have proposed to use neural networks with differentiable convex optimization layers to implement model predictive controllers. The motivation is to replace real-time optimization in safety critical feedback control systems with learnt mappings in the form of neural networks with optimization layers. Such mappings take as the input the state vector and predict the control law as the output. The learning takes place using training data generated from off-line MPC simulations. However, a general framework for characterization of learning approaches in terms of both model validation and efficient training data generation is lacking in literature. In this paper, we take the first steps towards developing such a coherent framework. We discuss how the learning problem has similarities with system identification, in particular input design, model structure selection and model validation. We consider the study of neural network architectures in PyTorch with the explicit MPC constraints implemented as a differentiable optimization layer using CVXPY. We propose an efficient approach of generating MPC input samples subject to the MPC model constraints using a hit-and-run sampler. The corresponding true outputs are generated by solving the MPC offline using OSOP. We propose different metrics to validate the resulting approaches. Our study further aims to explore the advantages of incorporating domain knowledge into the network structure from a training and evaluation perspective. Different model structures are numerically tested using the proposed framework in order to obtain more insights in the properties of constrained neural networks based MPC.