Francesco Dinuzzo
Predictive Response Optimization: Using Reinforcement Learning to Fight Online Social Network Abuse
Feb 24, 2025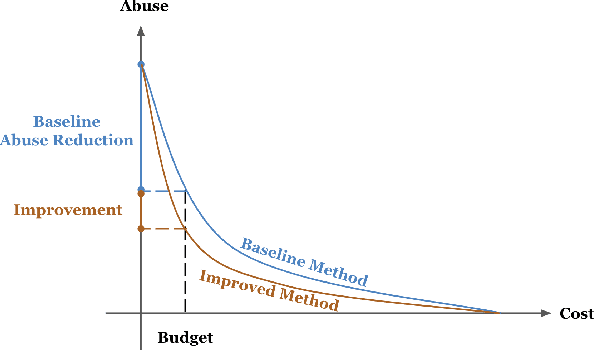

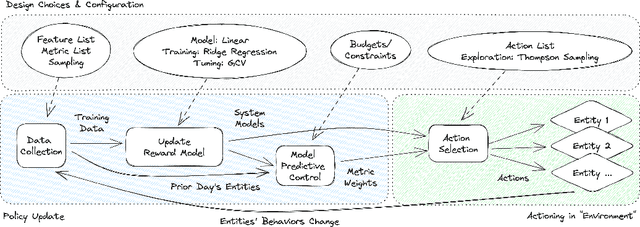
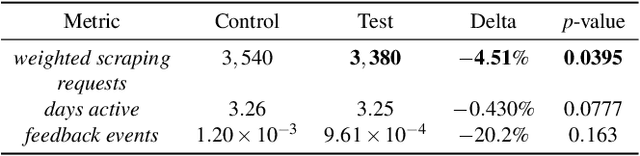
Abstract:Detecting phishing, spam, fake accounts, data scraping, and other malicious activity in online social networks (OSNs) is a problem that has been studied for well over a decade, with a number of important results. Nearly all existing works on abuse detection have as their goal producing the best possible binary classifier; i.e., one that labels unseen examples as "benign" or "malicious" with high precision and recall. However, no prior published work considers what comes next: what does the service actually do after it detects abuse? In this paper, we argue that detection as described in previous work is not the goal of those who are fighting OSN abuse. Rather, we believe the goal to be selecting actions (e.g., ban the user, block the request, show a CAPTCHA, or "collect more evidence") that optimize a tradeoff between harm caused by abuse and impact on benign users. With this framing, we see that enlarging the set of possible actions allows us to move the Pareto frontier in a way that is unattainable by simply tuning the threshold of a binary classifier. To demonstrate the potential of our approach, we present Predictive Response Optimization (PRO), a system based on reinforcement learning that utilizes available contextual information to predict future abuse and user-experience metrics conditioned on each possible action, and select actions that optimize a multi-dimensional tradeoff between abuse/harm and impact on user experience. We deployed versions of PRO targeted at stopping automated activity on Instagram and Facebook. In both cases our experiments showed that PRO outperforms a baseline classification system, reducing abuse volume by 59% and 4.5% (respectively) with no negative impact to users. We also present several case studies that demonstrate how PRO can quickly and automatically adapt to changes in business constraints, system behavior, and/or adversarial tactics.
Electricity Demand Forecasting by Multi-Task Learning
Dec 27, 2015



Abstract:We explore the application of kernel-based multi-task learning techniques to forecast the demand of electricity in multiple nodes of a distribution network. We show that recently developed output kernel learning techniques are particularly well suited to solve this problem, as they allow to flexibly model the complex seasonal effects that characterize electricity demand data, while learning and exploiting correlations between multiple demand profiles. We also demonstrate that kernels with a multiplicative structure yield superior predictive performance with respect to the widely adopted (generalized) additive models. Our study is based on residential and industrial smart meter data provided by the Irish Commission for Energy Regulation (CER).
Learning Output Kernels for Multi-Task Problems
Jan 16, 2013



Abstract:Simultaneously solving multiple related learning tasks is beneficial under a variety of circumstances, but the prior knowledge necessary to correctly model task relationships is rarely available in practice. In this paper, we develop a novel kernel-based multi-task learning technique that automatically reveals structural inter-task relationships. Building over the framework of output kernel learning (OKL), we introduce a method that jointly learns multiple functions and a low-rank multi-task kernel by solving a non-convex regularization problem. Optimization is carried out via a block coordinate descent strategy, where each subproblem is solved using suitable conjugate gradient (CG) type iterative methods for linear operator equations. The effectiveness of the proposed approach is demonstrated on pharmacological and collaborative filtering data.
Learning from Distributions via Support Measure Machines
Jan 12, 2013



Abstract:This paper presents a kernel-based discriminative learning framework on probability measures. Rather than relying on large collections of vectorial training examples, our framework learns using a collection of probability distributions that have been constructed to meaningfully represent training data. By representing these probability distributions as mean embeddings in the reproducing kernel Hilbert space (RKHS), we are able to apply many standard kernel-based learning techniques in straightforward fashion. To accomplish this, we construct a generalization of the support vector machine (SVM) called a support measure machine (SMM). Our analyses of SMMs provides several insights into their relationship to traditional SVMs. Based on such insights, we propose a flexible SVM (Flex-SVM) that places different kernel functions on each training example. Experimental results on both synthetic and real-world data demonstrate the effectiveness of our proposed framework.
The representer theorem for Hilbert spaces: a necessary and sufficient condition
Jul 17, 2012
Abstract:A family of regularization functionals is said to admit a linear representer theorem if every member of the family admits minimizers that lie in a fixed finite dimensional subspace. A recent characterization states that a general class of regularization functionals with differentiable regularizer admits a linear representer theorem if and only if the regularization term is a non-decreasing function of the norm. In this report, we improve over such result by replacing the differentiability assumption with lower semi-continuity and deriving a proof that is independent of the dimensionality of the space.
Fixed-point and coordinate descent algorithms for regularized kernel methods
Aug 30, 2010
Abstract:In this paper, we study two general classes of optimization algorithms for kernel methods with convex loss function and quadratic norm regularization, and analyze their convergence. The first approach, based on fixed-point iterations, is simple to implement and analyze, and can be easily parallelized. The second, based on coordinate descent, exploits the structure of additively separable loss functions to compute solutions of line searches in closed form. Instances of these general classes of algorithms are already incorporated into state of the art machine learning software for large scale problems. We start from a solution characterization of the regularized problem, obtained using sub-differential calculus and resolvents of monotone operators, that holds for general convex loss functions regardless of differentiability. The two methodologies described in the paper can be regarded as instances of non-linear Jacobi and Gauss-Seidel algorithms, and are both well-suited to solve large scale problems.
Kernel machines with two layers and multiple kernel learning
Jan 15, 2010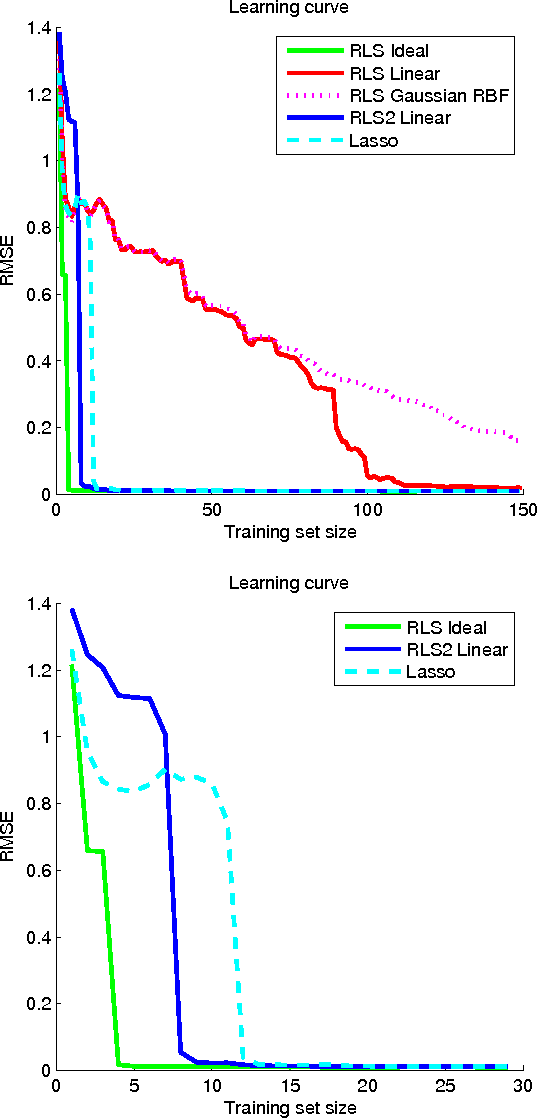
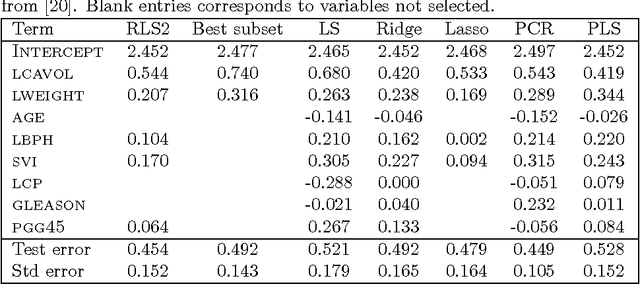
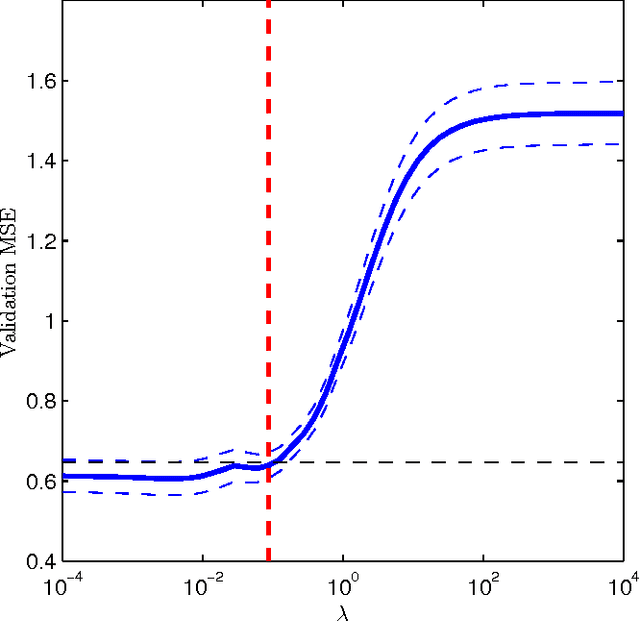
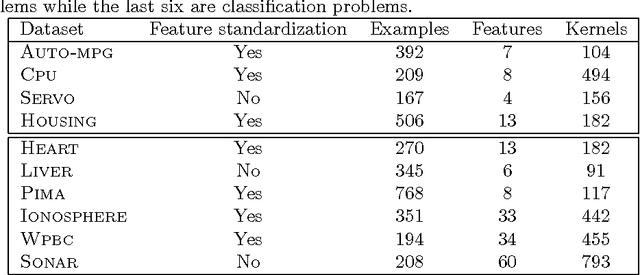
Abstract:In this paper, the framework of kernel machines with two layers is introduced, generalizing classical kernel methods. The new learning methodology provide a formal connection between computational architectures with multiple layers and the theme of kernel learning in standard regularization methods. First, a representer theorem for two-layer networks is presented, showing that finite linear combinations of kernels on each layer are optimal architectures whenever the corresponding functions solve suitable variational problems in reproducing kernel Hilbert spaces (RKHS). The input-output map expressed by these architectures turns out to be equivalent to a suitable single-layer kernel machines in which the kernel function is also learned from the data. Recently, the so-called multiple kernel learning methods have attracted considerable attention in the machine learning literature. In this paper, multiple kernel learning methods are shown to be specific cases of kernel machines with two layers in which the second layer is linear. Finally, a simple and effective multiple kernel learning method called RLS2 (regularized least squares with two layers) is introduced, and his performances on several learning problems are extensively analyzed. An open source MATLAB toolbox to train and validate RLS2 models with a Graphic User Interface is available.
Client-server multi-task learning from distributed datasets
Jan 11, 2010



Abstract:A client-server architecture to simultaneously solve multiple learning tasks from distributed datasets is described. In such architecture, each client is associated with an individual learning task and the associated dataset of examples. The goal of the architecture is to perform information fusion from multiple datasets while preserving privacy of individual data. The role of the server is to collect data in real-time from the clients and codify the information in a common database. The information coded in this database can be used by all the clients to solve their individual learning task, so that each client can exploit the informative content of all the datasets without actually having access to private data of others. The proposed algorithmic framework, based on regularization theory and kernel methods, uses a suitable class of mixed effect kernels. The new method is illustrated through a simulated music recommendation system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge