Kernel machines with two layers and multiple kernel learning
Paper and Code
Jan 15, 2010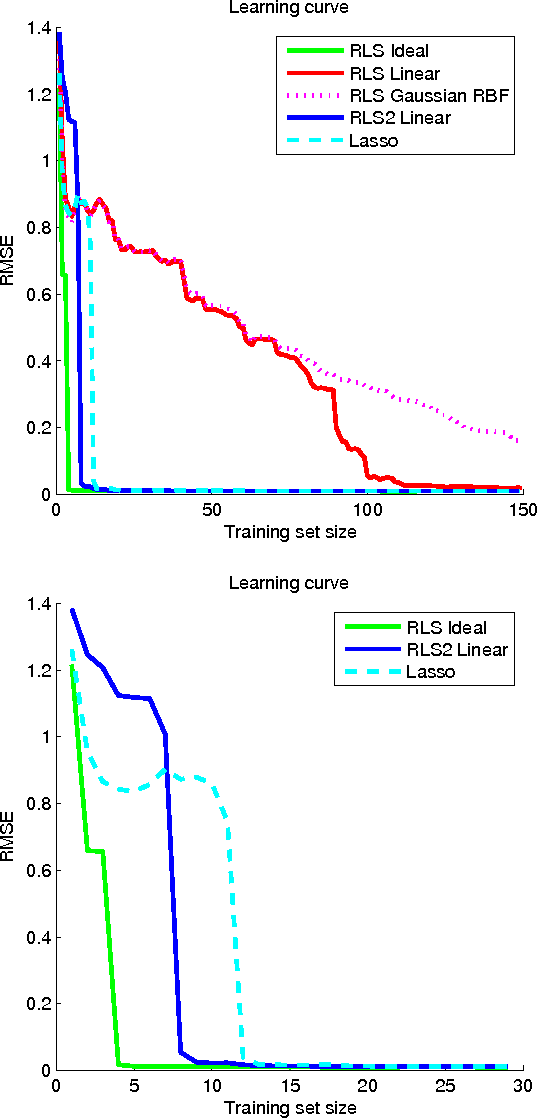
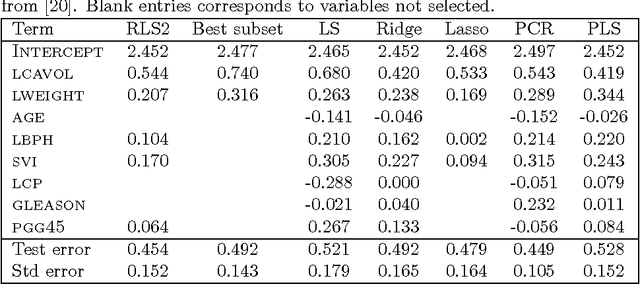
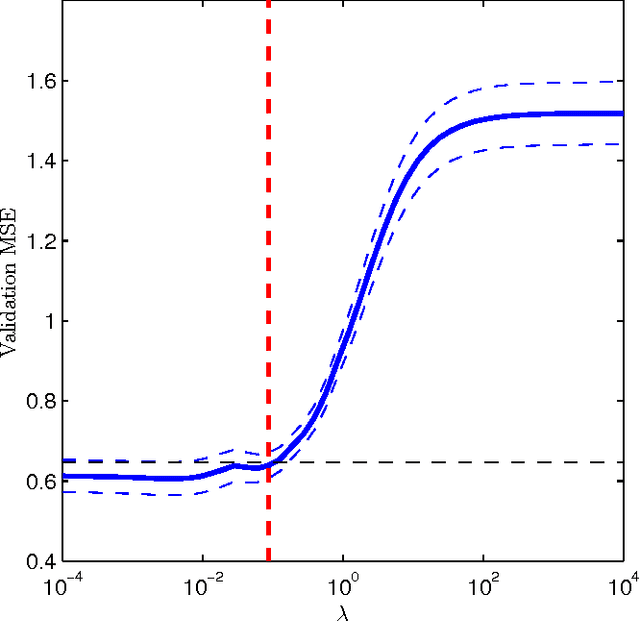
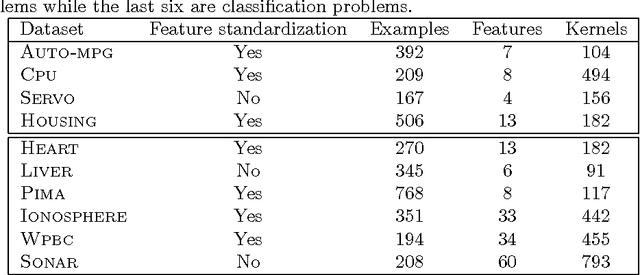
In this paper, the framework of kernel machines with two layers is introduced, generalizing classical kernel methods. The new learning methodology provide a formal connection between computational architectures with multiple layers and the theme of kernel learning in standard regularization methods. First, a representer theorem for two-layer networks is presented, showing that finite linear combinations of kernels on each layer are optimal architectures whenever the corresponding functions solve suitable variational problems in reproducing kernel Hilbert spaces (RKHS). The input-output map expressed by these architectures turns out to be equivalent to a suitable single-layer kernel machines in which the kernel function is also learned from the data. Recently, the so-called multiple kernel learning methods have attracted considerable attention in the machine learning literature. In this paper, multiple kernel learning methods are shown to be specific cases of kernel machines with two layers in which the second layer is linear. Finally, a simple and effective multiple kernel learning method called RLS2 (regularized least squares with two layers) is introduced, and his performances on several learning problems are extensively analyzed. An open source MATLAB toolbox to train and validate RLS2 models with a Graphic User Interface is available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge