Visual Representations: Defining Properties and Deep Approximations
Paper and Code
Feb 29, 2016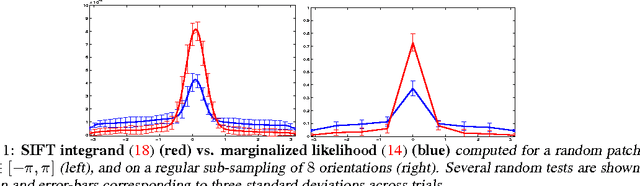


Visual representations are defined in terms of minimal sufficient statistics of visual data, for a class of tasks, that are also invariant to nuisance variability. Minimal sufficiency guarantees that we can store a representation in lieu of raw data with smallest complexity and no performance loss on the task at hand. Invariance guarantees that the statistic is constant with respect to uninformative transformations of the data. We derive analytical expressions for such representations and show they are related to feature descriptors commonly used in computer vision, as well as to convolutional neural networks. This link highlights the assumptions and approximations tacitly assumed by these methods and explains empirical practices such as clamping, pooling and joint normalization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge