Identification of Non-causal Graphical Models

The paper considers the problem to estimate non-causal graphical models whose edges encode smoothing relations among the variables. We propose a new covariance extension problem and show that the solution minimizing the transportation distance with respect to white noise process is a double-sided autoregressive non-causal graphical model. Then, we generalize the paradigm to a class of graphical autoregressive moving-average models. Finally, we test the performance of the proposed method through some numerical experiments.

On the Statistical Consistency of a Generalized Cepstral Estimator

We consider the problem to estimate the generalized cepstral coefficients of a stationary stochastic process or stationary multidimensional random field. It turns out that a naive version of the periodogram-based estimator for the generalized cepstral coefficients is not consistent. We propose a consistent estimator for those coefficients. Moreover, we show that the latter can be used in order to build a consistent estimator for a particular class of cascade linear stochastic systems.

Autoregressive Identification of Kronecker Graphical Models

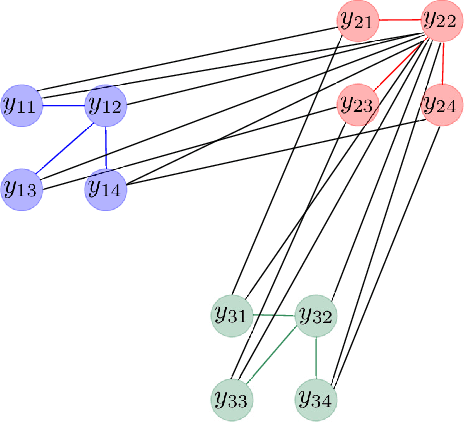
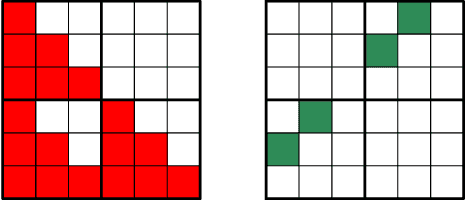
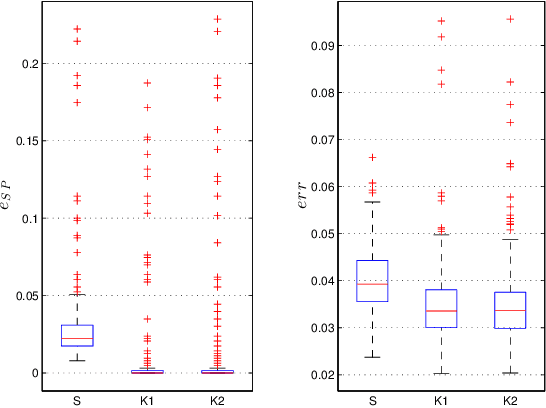
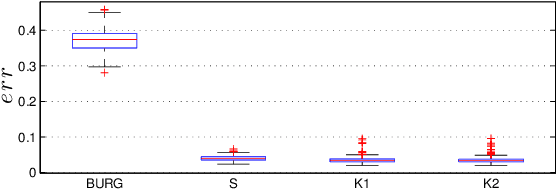
We address the problem to estimate a Kronecker graphical model corresponding to an autoregressive Gaussian stochastic process. The latter is completely described by the power spectral density function whose inverse has support which admits a Kronecker product decomposition. We propose a Bayesian approach to estimate such a model. We test the effectiveness of the proposed method by some numerical experiments. We also apply the procedure to urban pollution monitoring data.

Derivative-free online learning of inverse dynamics models

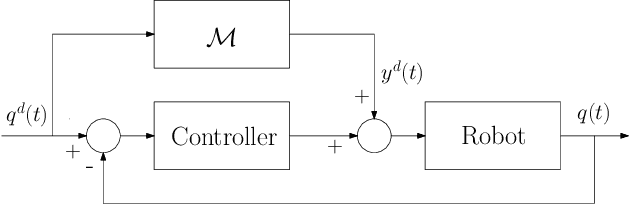
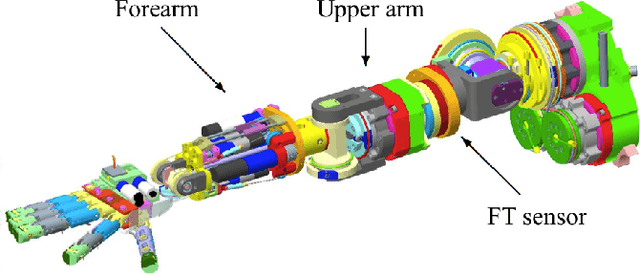
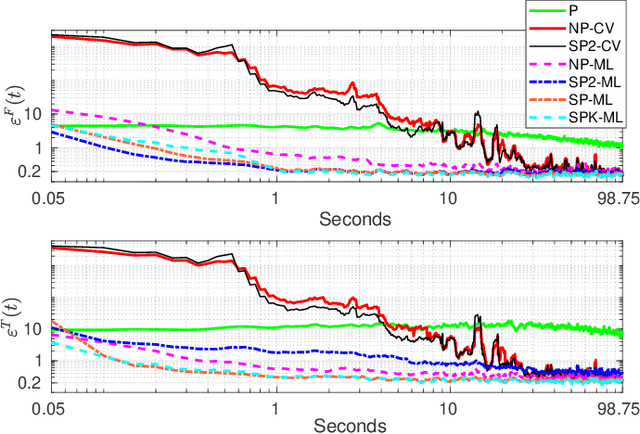
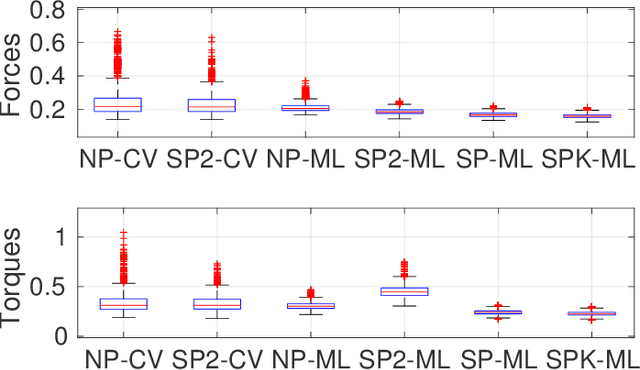
This paper discusses online algorithms for inverse dynamics modelling in robotics. Several model classes including rigid body dynamics (RBD) models, data-driven models and semiparametric models (which are a combination of the previous two classes) are placed in a common framework. While model classes used in the literature typically exploit joint velocities and accelerations, which need to be approximated resorting to numerical differentiation schemes, in this paper a new `derivative-free' framework is proposed that does not require this preprocessing step. An extensive experimental study with real data from the right arm of the iCub robot is presented, comparing different model classes and estimation procedures, showing that the proposed `derivative-free' methods outperform existing methodologies.

Online semi-parametric learning for inverse dynamics modeling

This paper presents a semi-parametric algorithm for online learning of a robot inverse dynamics model. It combines the strength of the parametric and non-parametric modeling. The former exploits the rigid body dynamics equa- tion, while the latter exploits a suitable kernel function. We provide an extensive comparison with other methods from the literature using real data from the iCub humanoid robot. In doing so we also compare two different techniques, namely cross validation and marginal likelihood optimization, for estimating the hyperparameters of the kernel function.

A Bayesian Approach to Sparse plus Low rank Network Identification

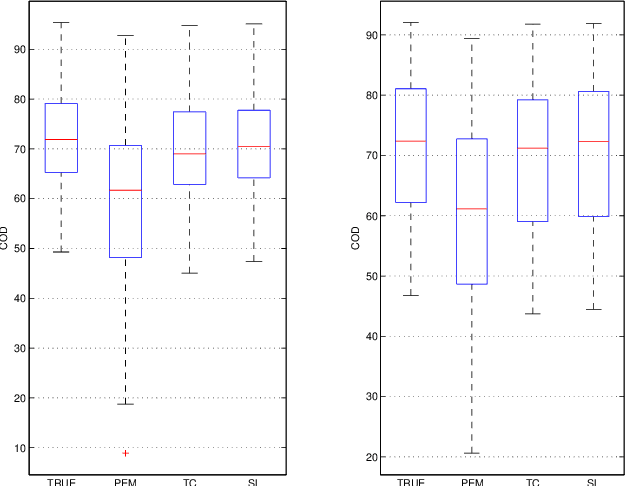
We consider the problem of modeling multivariate time series with parsimonious dynamical models which can be represented as sparse dynamic Bayesian networks with few latent nodes. This structure translates into a sparse plus low rank model. In this paper, we propose a Gaussian regression approach to identify such a model.

Sparse plus low-rank autoregressive identification in neuroimaging time series

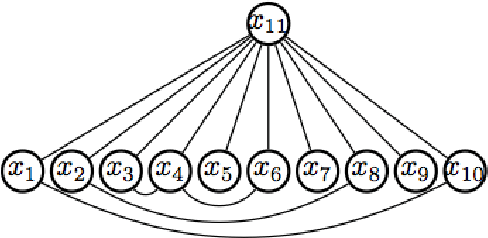
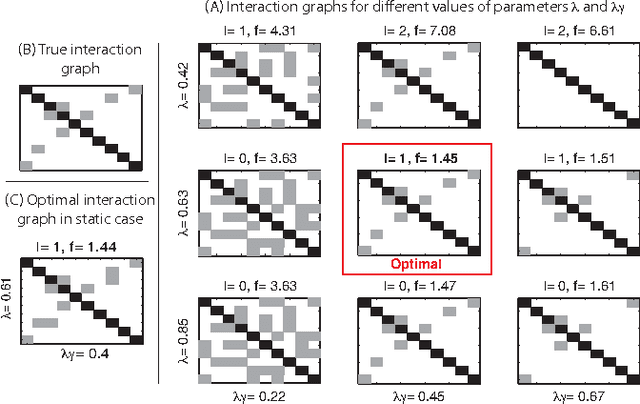
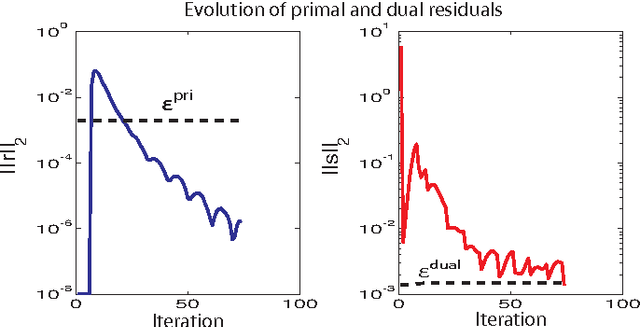
This paper considers the problem of identifying multivariate autoregressive (AR) sparse plus low-rank graphical models. Based on the corresponding problem formulation recently presented, we use the alternating direction method of multipliers (ADMM) to efficiently solve it and scale it to sizes encountered in neuroimaging applications. We apply this decomposition on synthetic and real neuroimaging datasets with a specific focus on the information encoded in the low-rank structure of our model. In particular, we illustrate that this information captures the spatio-temporal structure of the original data, generalizing classical component analysis approaches.