Sparse plus low-rank autoregressive identification in neuroimaging time series
Paper and Code
Mar 30, 2015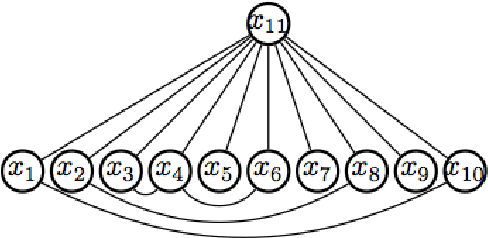
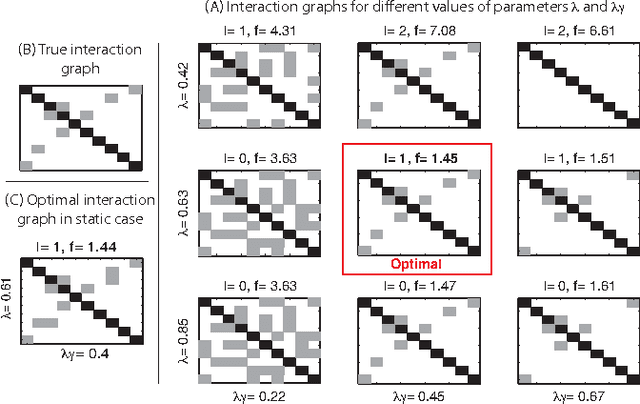
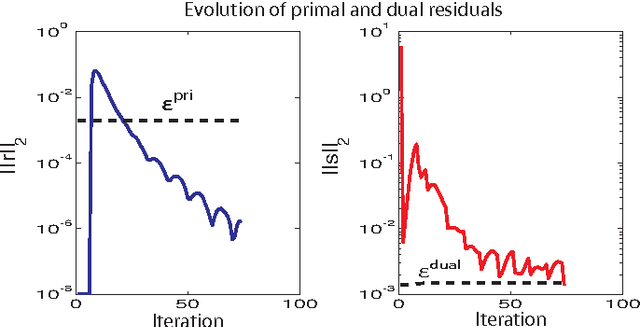
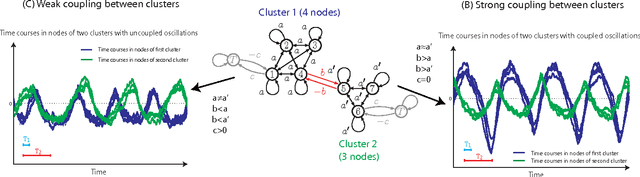
This paper considers the problem of identifying multivariate autoregressive (AR) sparse plus low-rank graphical models. Based on the corresponding problem formulation recently presented, we use the alternating direction method of multipliers (ADMM) to efficiently solve it and scale it to sizes encountered in neuroimaging applications. We apply this decomposition on synthetic and real neuroimaging datasets with a specific focus on the information encoded in the low-rank structure of our model. In particular, we illustrate that this information captures the spatio-temporal structure of the original data, generalizing classical component analysis approaches.
* 6 pages paper submitted to CDC 2015
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge