Guided Graph Spectral Embedding: Application to the C. elegans Connectome

Graph spectral analysis can yield meaningful embeddings of graphs by providing insight into distributed features not directly accessible in nodal domain. Recent efforts in graph signal processing have proposed new decompositions-e.g., based on wavelets and Slepians-that can be applied to filter signals defined on the graph. In this work, we take inspiration from these constructions to define a new guided spectral embedding that combines maximizing energy concentration with minimizing modified embedded distance for a given importance weighting of the nodes. We show these optimization goals are intrinsically opposite, leading to a well-defined and stable spectral decomposition. The importance weighting allows to put the focus on particular nodes and tune the trade-off between global and local effects. Following the derivation of our new optimization criterion and its linear approximation, we exemplify the methodology on the C. elegans structural connectome. The results of our analyses confirm known observations on the nematode's neural network in terms of functionality and importance of cells. Compared to Laplacian embedding, the guided approach, focused on a certain class of cells (sensory, inter- and motoneurons), provides more biological insights, such as the distinction between somatic positions of cells, and their involvement in low or high order processing functions.

Sparse plus low-rank autoregressive identification in neuroimaging time series

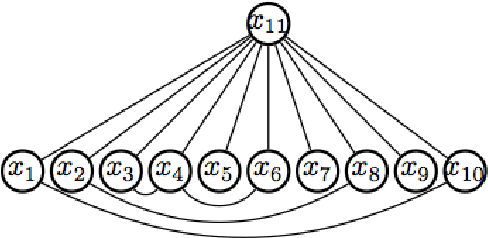
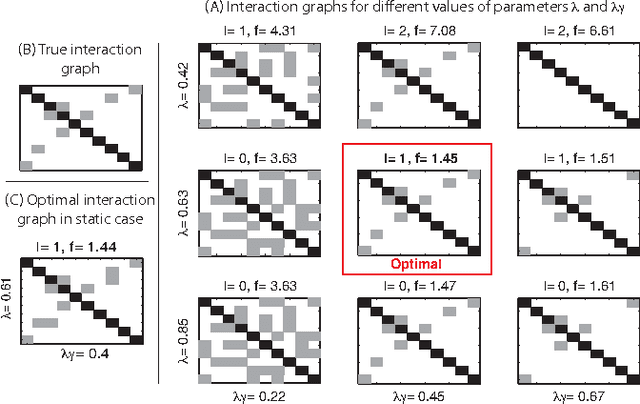
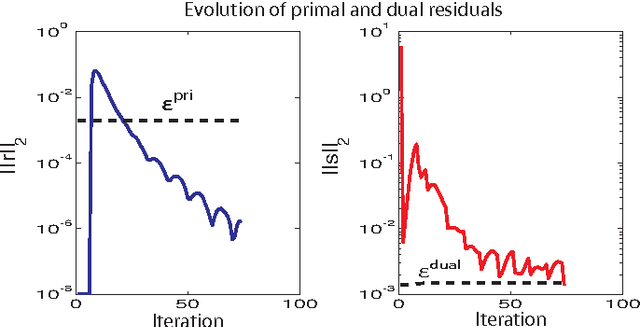
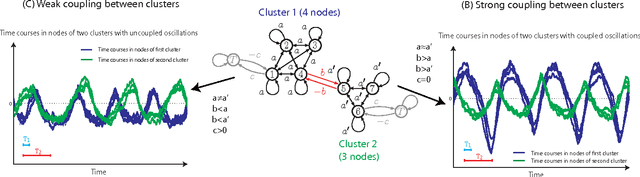
This paper considers the problem of identifying multivariate autoregressive (AR) sparse plus low-rank graphical models. Based on the corresponding problem formulation recently presented, we use the alternating direction method of multipliers (ADMM) to efficiently solve it and scale it to sizes encountered in neuroimaging applications. We apply this decomposition on synthetic and real neuroimaging datasets with a specific focus on the information encoded in the low-rank structure of our model. In particular, we illustrate that this information captures the spatio-temporal structure of the original data, generalizing classical component analysis approaches.