Autoregressive Identification of Kronecker Graphical Models
Paper and Code
Apr 29, 2020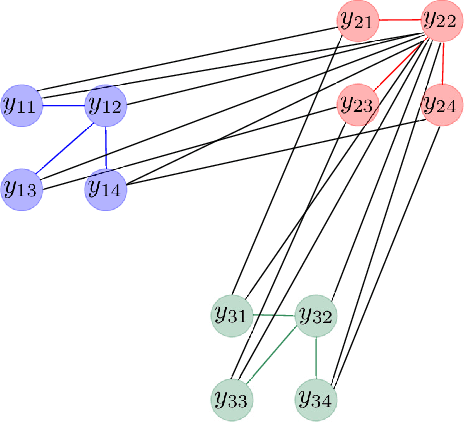
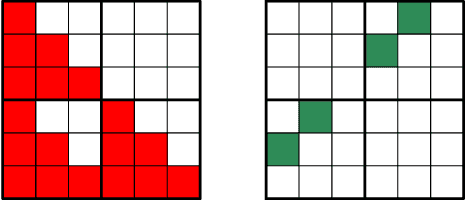
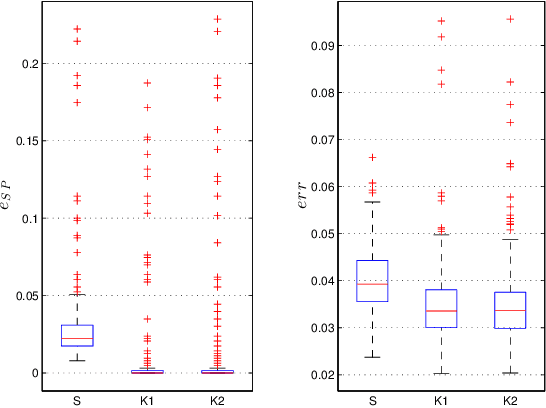
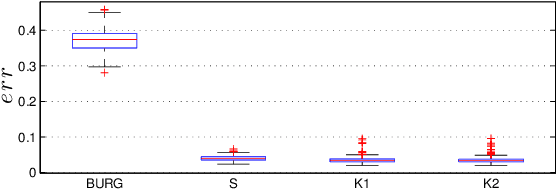
We address the problem to estimate a Kronecker graphical model corresponding to an autoregressive Gaussian stochastic process. The latter is completely described by the power spectral density function whose inverse has support which admits a Kronecker product decomposition. We propose a Bayesian approach to estimate such a model. We test the effectiveness of the proposed method by some numerical experiments. We also apply the procedure to urban pollution monitoring data.
* Automatica (accepted)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge