Adapting, Fast and Slow: Transportable Circuits for Few-Shot Learning

Generalization across the domains is not possible without asserting a structure that constrains the unseen target domain w.r.t. the source domain. Building on causal transportability theory, we design an algorithm for zero-shot compositional generalization which relies on access to qualitative domain knowledge in form of a causal graph for intra-domain structure and discrepancies oracle for inter-domain mechanism sharing. \textit{Circuit-TR} learns a collection of modules (i.e., local predictors) from the source data, and transport/compose them to obtain a circuit for prediction in the target domain if the causal structure licenses. Furthermore, circuit transportability enables us to design a supervised domain adaptation scheme that operates without access to an explicit causal structure, and instead uses limited target data. Our theoretical results characterize classes of few-shot learnable tasks in terms of graphical circuit transportability criteria, and connects few-shot generalizability with the established notion of circuit size complexity; controlled simulations corroborate our theoretical results.

Multi-Domain Causal Discovery in Bijective Causal Models

We consider the problem of causal discovery (a.k.a., causal structure learning) in a multi-domain setting. We assume that the causal functions are invariant across the domains, while the distribution of the exogenous noise may vary. Under causal sufficiency (i.e., no confounders exist), we show that the causal diagram can be discovered under less restrictive functional assumptions compared to previous work. What enables causal discovery in this setting is bijective generation mechanisms (BGM), which ensures that the functional relation between the exogenous noise $E$ and the endogenous variable $Y$ is bijective and differentiable in both directions at every level of the cause variable $X = x$. BGM generalizes a variety of models including additive noise model, LiNGAM, post-nonlinear model, and location-scale noise model. Further, we derive a statistical test to find the parents set of the target variable. Experiments on various synthetic and real-world datasets validate our theoretical findings.

Partial Transportability for Domain Generalization

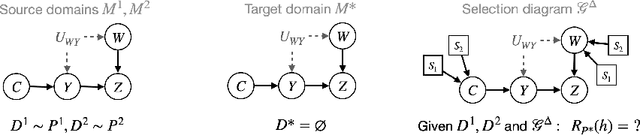
A fundamental task in AI is providing performance guarantees for predictions made in unseen domains. In practice, there can be substantial uncertainty about the distribution of new data, and corresponding variability in the performance of existing predictors. Building on the theory of partial identification and transportability, this paper introduces new results for bounding the value of a functional of the target distribution, such as the generalization error of a classifier, given data from source domains and assumptions about the data generating mechanisms, encoded in causal diagrams. Our contribution is to provide the first general estimation technique for transportability problems, adapting existing parameterization schemes such Neural Causal Models to encode the structural constraints necessary for cross-population inference. We demonstrate the expressiveness and consistency of this procedure and further propose a gradient-based optimization scheme for making scalable inferences in practice. Our results are corroborated with experiments.