Saber Salehkaleybar
Causal Effect Identification in Heterogeneous Environments from Higher-Order Moments
Jun 13, 2025Abstract:We investigate the estimation of the causal effect of a treatment variable on an outcome in the presence of a latent confounder. We first show that the causal effect is identifiable under certain conditions when data is available from multiple environments, provided that the target causal effect remains invariant across these environments. Secondly, we propose a moment-based algorithm for estimating the causal effect as long as only a single parameter of the data-generating mechanism varies across environments -- whether it be the exogenous noise distribution or the causal relationship between two variables. Conversely, we prove that identifiability is lost if both exogenous noise distributions of both the latent and treatment variables vary across environments. Finally, we propose a procedure to identify which parameter of the data-generating mechanism has varied across the environments and evaluate the performance of our proposed methods through experiments on synthetic data.
Causal Effect Identification in lvLiNGAM from Higher-Order Cumulants
Jun 06, 2025Abstract:This paper investigates causal effect identification in latent variable Linear Non-Gaussian Acyclic Models (lvLiNGAM) using higher-order cumulants, addressing two prominent setups that are challenging in the presence of latent confounding: (1) a single proxy variable that may causally influence the treatment and (2) underspecified instrumental variable cases where fewer instruments exist than treatments. We prove that causal effects are identifiable with a single proxy or instrument and provide corresponding estimation methods. Experimental results demonstrate the accuracy and robustness of our approaches compared to existing methods, advancing the theoretical and practical understanding of causal inference in linear systems with latent confounders.
Multi-Domain Causal Discovery in Bijective Causal Models
Apr 30, 2025Abstract:We consider the problem of causal discovery (a.k.a., causal structure learning) in a multi-domain setting. We assume that the causal functions are invariant across the domains, while the distribution of the exogenous noise may vary. Under causal sufficiency (i.e., no confounders exist), we show that the causal diagram can be discovered under less restrictive functional assumptions compared to previous work. What enables causal discovery in this setting is bijective generation mechanisms (BGM), which ensures that the functional relation between the exogenous noise $E$ and the endogenous variable $Y$ is bijective and differentiable in both directions at every level of the cause variable $X = x$. BGM generalizes a variety of models including additive noise model, LiNGAM, post-nonlinear model, and location-scale noise model. Further, we derive a statistical test to find the parents set of the target variable. Experiments on various synthetic and real-world datasets validate our theoretical findings.
ACTIVA: Amortized Causal Effect Estimation without Graphs via Transformer-based Variational Autoencoder
Mar 03, 2025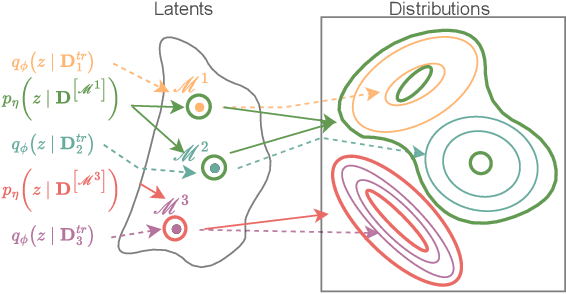
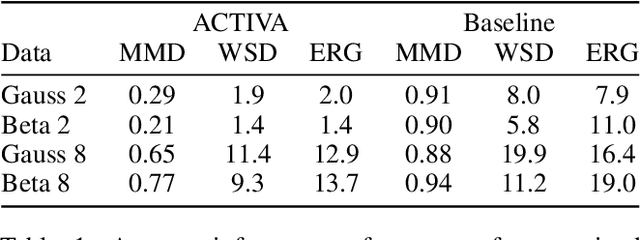
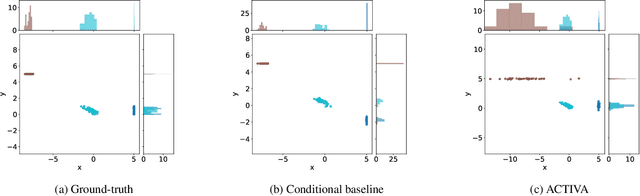

Abstract:Predicting the distribution of outcomes under hypothetical interventions is crucial in domains like healthcare, economics, and policy-making. Current methods often rely on strong assumptions, such as known causal graphs or parametric models, and lack amortization across problem instances, limiting their practicality. We propose a novel transformer-based conditional variational autoencoder architecture, named ACTIVA, that extends causal transformer encoders to predict causal effects as mixtures of Gaussians. Our method requires no causal graph and predicts interventional distributions given only observational data and a queried intervention. By amortizing over many simulated instances, it enables zero-shot generalization to novel datasets without retraining. Experiments demonstrate accurate predictions for synthetic and semi-synthetic data, showcasing the effectiveness of our graph-free, amortized causal inference approach.
Complexity of Minimizing Projected-Gradient-Dominated Functions with Stochastic First-order Oracles
Aug 03, 2024
Abstract:This work investigates the performance limits of projected stochastic first-order methods for minimizing functions under the $(\alpha,\tau,\mathcal{X})$-projected-gradient-dominance property, that asserts the sub-optimality gap $F(\mathbf{x})-\min_{\mathbf{x}'\in \mathcal{X}}F(\mathbf{x}')$ is upper-bounded by $\tau\cdot\|\mathcal{G}_{\eta,\mathcal{X}}(\mathbf{x})\|^{\alpha}$ for some $\alpha\in[1,2)$ and $\tau>0$ and $\mathcal{G}_{\eta,\mathcal{X}}(\mathbf{x})$ is the projected-gradient mapping with $\eta>0$ as a parameter. For non-convex functions, we show that the complexity lower bound of querying a batch smooth first-order stochastic oracle to obtain an $\epsilon$-global-optimum point is $\Omega(\epsilon^{-{2}/{\alpha}})$. Furthermore, we show that a projected variance-reduced first-order algorithm can obtain the upper complexity bound of $\mathcal{O}(\epsilon^{-{2}/{\alpha}})$, matching the lower bound. For convex functions, we establish a complexity lower bound of $\Omega(\log(1/\epsilon)\cdot\epsilon^{-{2}/{\alpha}})$ for minimizing functions under a local version of gradient-dominance property, which also matches the upper complexity bound of accelerated stochastic subgradient methods.
Causal Effect Identification in LiNGAM Models with Latent Confounders
Jun 04, 2024



Abstract:We study the generic identifiability of causal effects in linear non-Gaussian acyclic models (LiNGAM) with latent variables. We consider the problem in two main settings: When the causal graph is known a priori, and when it is unknown. In both settings, we provide a complete graphical characterization of the identifiable direct or total causal effects among observed variables. Moreover, we propose efficient algorithms to certify the graphical conditions. Finally, we propose an adaptation of the reconstruction independent component analysis (RICA) algorithm that estimates the causal effects from the observational data given the causal graph. Experimental results show the effectiveness of the proposed method in estimating the causal effects.
Soft Preference Optimization: Aligning Language Models to Expert Distributions
Apr 30, 2024
Abstract:We propose Soft Preference Optimization (SPO), a method for aligning generative models, such as Large Language Models (LLMs), with human preferences, without the need for a reward model. SPO optimizes model outputs directly over a preference dataset through a natural loss function that integrates preference loss with a regularization term across the model's entire output distribution rather than limiting it to the preference dataset. Although SPO does not require the assumption of an existing underlying reward model, we demonstrate that, under the Bradley-Terry (BT) model assumption, it converges to a softmax of scaled rewards, with the distribution's "softness" adjustable via the softmax exponent, an algorithm parameter. We showcase SPO's methodology, its theoretical foundation, and its comparative advantages in simplicity, computational efficiency, and alignment precision.
MetaOptimize: A Framework for Optimizing Step Sizes and Other Meta-parameters
Feb 12, 2024



Abstract:This paper addresses the challenge of optimizing meta-parameters (i.e., hyperparameters) in machine learning algorithms, a critical factor influencing training efficiency and model performance. Moving away from the computationally expensive traditional meta-parameter search methods, we introduce MetaOptimize framework that dynamically adjusts meta-parameters, particularly step sizes (also known as learning rates), during training. More specifically, MetaOptimize can wrap around any first-order optimization algorithm, tuning step sizes on the fly to minimize a specific form of regret that accounts for long-term effect of step sizes on training, through a discounted sum of future losses. We also introduce low complexity variants of MetaOptimize that, in conjunction with its adaptability to multiple optimization algorithms, demonstrate performance competitive to those of best hand-crafted learning rate schedules across various machine learning applications.
Learning Unknown Intervention Targets in Structural Causal Models from Heterogeneous Data
Dec 11, 2023



Abstract:We study the problem of identifying the unknown intervention targets in structural causal models where we have access to heterogeneous data collected from multiple environments. The unknown intervention targets are the set of endogenous variables whose corresponding exogenous noises change across the environments. We propose a two-phase approach which in the first phase recovers the exogenous noises corresponding to unknown intervention targets whose distributions have changed across environments. In the second phase, the recovered noises are matched with the corresponding endogenous variables. For the recovery phase, we provide sufficient conditions for learning these exogenous noises up to some component-wise invertible transformation. For the matching phase, under the causal sufficiency assumption, we show that the proposed method uniquely identifies the intervention targets. In the presence of latent confounders, the intervention targets among the observed variables cannot be determined uniquely. We provide a candidate intervention target set which is a superset of the true intervention targets. Our approach improves upon the state of the art as the returned candidate set is always a subset of the target set returned by previous work. Moreover, we do not require restrictive assumptions such as linearity of the causal model or performing invariance tests to learn whether a distribution is changing across environments which could be highly sample inefficient. Our experimental results show the effectiveness of our proposed algorithm in practice.
Efficiently Escaping Saddle Points for Non-Convex Policy Optimization
Nov 15, 2023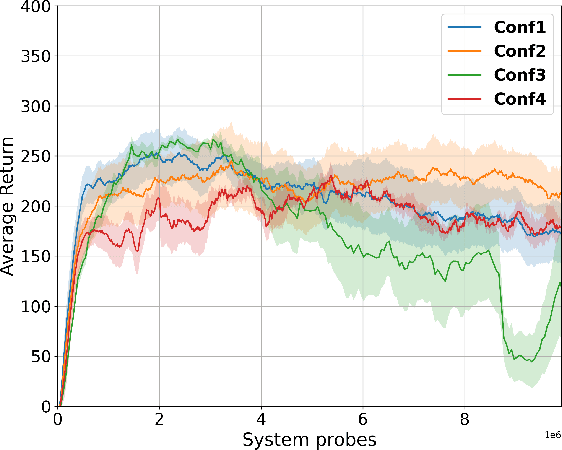
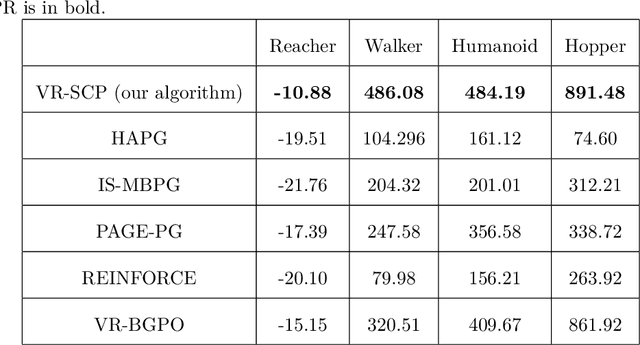
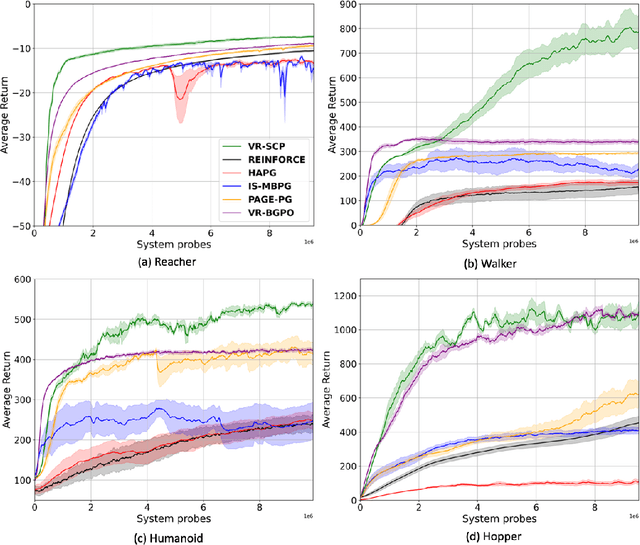
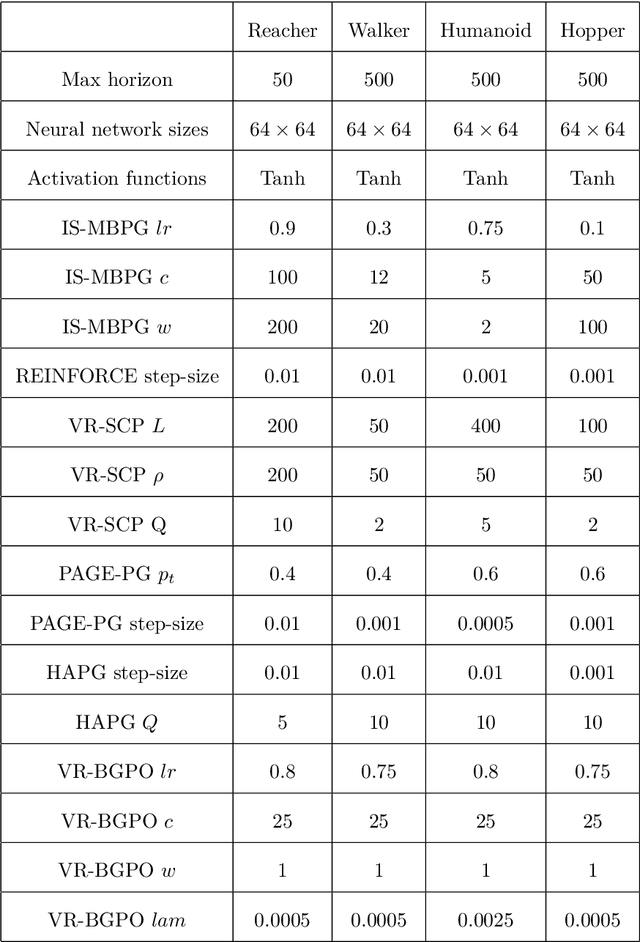
Abstract:Policy gradient (PG) is widely used in reinforcement learning due to its scalability and good performance. In recent years, several variance-reduced PG methods have been proposed with a theoretical guarantee of converging to an approximate first-order stationary point (FOSP) with the sample complexity of $O(\epsilon^{-3})$. However, FOSPs could be bad local optima or saddle points. Moreover, these algorithms often use importance sampling (IS) weights which could impair the statistical effectiveness of variance reduction. In this paper, we propose a variance-reduced second-order method that uses second-order information in the form of Hessian vector products (HVP) and converges to an approximate second-order stationary point (SOSP) with sample complexity of $\tilde{O}(\epsilon^{-3})$. This rate improves the best-known sample complexity for achieving approximate SOSPs by a factor of $O(\epsilon^{-0.5})$. Moreover, the proposed variance reduction technique bypasses IS weights by using HVP terms. Our experimental results show that the proposed algorithm outperforms the state of the art and is more robust to changes in random seeds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge