Recycling History: Efficient Recommendations from Contextual Dueling Bandits

The contextual duelling bandit problem models adaptive recommender systems, where the algorithm presents a set of items to the user, and the user's choice reveals their preference. This setup is well suited for implicit choices users make when navigating a content platform, but does not capture other possible comparison queries. Motivated by the fact that users provide more reliable feedback after consuming items, we propose a new bandit model that can be described as follows. The algorithm recommends one item per time step; after consuming that item, the user is asked to compare it with another item chosen from the user's consumption history. Importantly, in our model, this comparison item can be chosen without incurring any additional regret, potentially leading to better performance. However, the regret analysis is challenging because of the temporal dependency in the user's history. To overcome this challenge, we first show that the algorithm can construct informative queries provided the history is rich, i.e., satisfies a certain diversity condition. We then show that a short initial random exploration phase is sufficient for the algorithm to accumulate a rich history with high probability. This result, proven via matrix concentration bounds, yields $O(\sqrt{T})$ regret guarantees. Additionally, our simulations show that reusing past items for comparisons can lead to significantly lower regret than only comparing between simultaneously recommended items.

Measuring IIA Violations in Similarity Choices with Bayesian Models

Similarity choice data occur when humans make choices among alternatives based on their similarity to a target, e.g., in the context of information retrieval and in embedding learning settings. Classical metric-based models of similarity choice assume independence of irrelevant alternatives (IIA), a property that allows for a simpler formulation. While IIA violations have been detected in many discrete choice settings, the similarity choice setting has received scant attention. This is because the target-dependent nature of the choice complicates IIA testing. We propose two statistical methods to test for IIA: a classical goodness-of-fit test and a Bayesian counterpart based on the framework of Posterior Predictive Checks (PPC). This Bayesian approach, our main technical contribution, quantifies the degree of IIA violation beyond its mere significance. We curate two datasets: one with choice sets designed to elicit IIA violations, and another with randomly generated choice sets from the same item universe. Our tests confirmed significant IIA violations on both datasets, and notably, we find a comparable degree of violation between them. Further, we devise a new PPC test for population homogeneity. Results show that the population is indeed homogenous, suggesting that the IIA violations are driven by context effects -- specifically, interactions within the choice sets. These results highlight the need for new similarity choice models that account for such context effects.

Recommendations from Sparse Comparison Data: Provably Fast Convergence for Nonconvex Matrix Factorization

This paper provides a theoretical analysis of a new learning problem for recommender systems where users provide feedback by comparing pairs of items instead of rating them individually. We assume that comparisons stem from latent user and item features, which reduces the task of predicting preferences to learning these features from comparison data. Similar to the classical matrix factorization problem, the main challenge in this learning task is that the resulting loss function is nonconvex. Our analysis shows that the loss function exhibits (restricted) strong convexity near the true solution, which ensures gradient-based methods converge exponentially, given an appropriate warm start. Importantly, this result holds in a sparse data regime, where each user compares only a few pairs of items. Our main technical contribution is to extend certain concentration inequalities commonly used in matrix completion to our model. Our work demonstrates that learning personalized recommendations from comparison data is computationally and statistically efficient.

Why the Metric Backbone Preserves Community Structure

The metric backbone of a weighted graph is the union of all-pairs shortest paths. It is obtained by removing all edges $(u,v)$ that are not the shortest path between $u$ and $v$. In networks with well-separated communities, the metric backbone tends to preserve many inter-community edges, because these edges serve as bridges connecting two communities, but tends to delete many intra-community edges because the communities are dense. This suggests that the metric backbone would dilute or destroy the community structure of the network. However, this is not borne out by prior empirical work, which instead showed that the metric backbone of real networks preserves the community structure of the original network well. In this work, we analyze the metric backbone of a broad class of weighted random graphs with communities, and we formally prove the robustness of the community structure with respect to the deletion of all the edges that are not in the metric backbone. An empirical comparison of several graph sparsification techniques confirms our theoretical finding and shows that the metric backbone is an efficient sparsifier in the presence of communities.

Causal Effect Identification in a Sub-Population with Latent Variables

The s-ID problem seeks to compute a causal effect in a specific sub-population from the observational data pertaining to the same sub population (Abouei et al., 2023). This problem has been addressed when all the variables in the system are observable. In this paper, we consider an extension of the s-ID problem that allows for the presence of latent variables. To tackle the challenges induced by the presence of latent variables in a sub-population, we first extend the classical relevant graphical definitions, such as c-components and Hedges, initially defined for the so-called ID problem (Pearl, 1995; Tian & Pearl, 2002), to their new counterparts. Subsequently, we propose a sound algorithm for the s-ID problem with latent variables.

Universal Lower Bounds and Optimal Rates: Achieving Minimax Clustering Error in Sub-Exponential Mixture Models

Clustering is a pivotal challenge in unsupervised machine learning and is often investigated through the lens of mixture models. The optimal error rate for recovering cluster labels in Gaussian and sub-Gaussian mixture models involves ad hoc signal-to-noise ratios. Simple iterative algorithms, such as Lloyd's algorithm, attain this optimal error rate. In this paper, we first establish a universal lower bound for the error rate in clustering any mixture model, expressed through a Chernoff divergence, a more versatile measure of model information than signal-to-noise ratios. We then demonstrate that iterative algorithms attain this lower bound in mixture models with sub-exponential tails, notably emphasizing location-scale mixtures featuring Laplace-distributed errors. Additionally, for datasets better modelled by Poisson or Negative Binomial mixtures, we study mixture models whose distributions belong to an exponential family. In such mixtures, we establish that Bregman hard clustering, a variant of Lloyd's algorithm employing a Bregman divergence, is rate optimal.

Efficiently Escaping Saddle Points for Non-Convex Policy Optimization

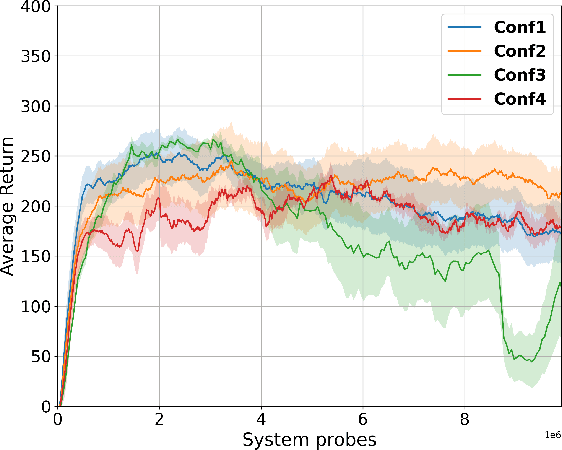
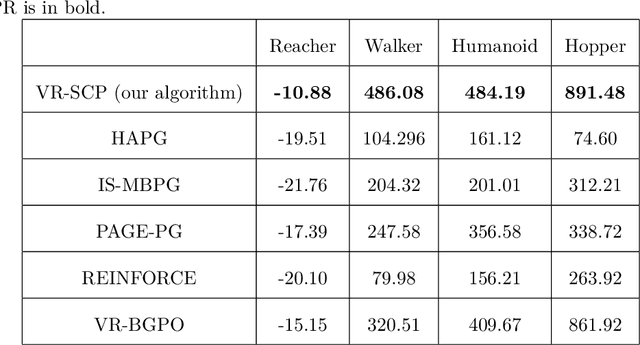
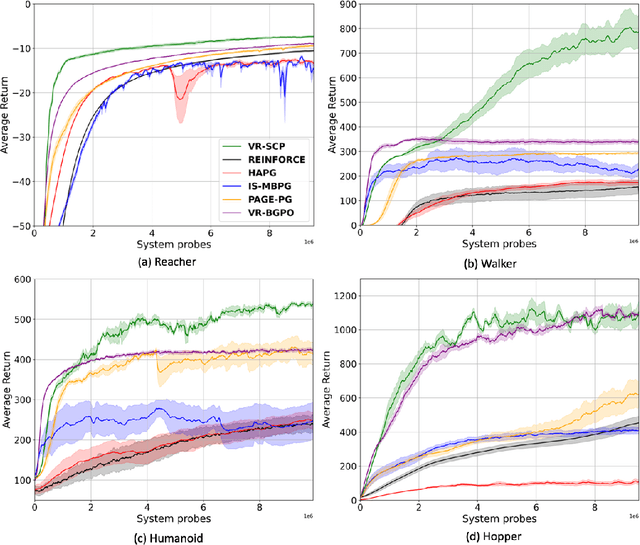
Policy gradient (PG) is widely used in reinforcement learning due to its scalability and good performance. In recent years, several variance-reduced PG methods have been proposed with a theoretical guarantee of converging to an approximate first-order stationary point (FOSP) with the sample complexity of $O(\epsilon^{-3})$. However, FOSPs could be bad local optima or saddle points. Moreover, these algorithms often use importance sampling (IS) weights which could impair the statistical effectiveness of variance reduction. In this paper, we propose a variance-reduced second-order method that uses second-order information in the form of Hessian vector products (HVP) and converges to an approximate second-order stationary point (SOSP) with sample complexity of $\tilde{O}(\epsilon^{-3})$. This rate improves the best-known sample complexity for achieving approximate SOSPs by a factor of $O(\epsilon^{-0.5})$. Moreover, the proposed variance reduction technique bypasses IS weights by using HVP terms. Our experimental results show that the proposed algorithm outperforms the state of the art and is more robust to changes in random seeds.

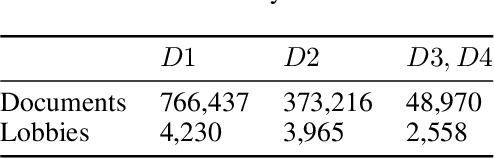
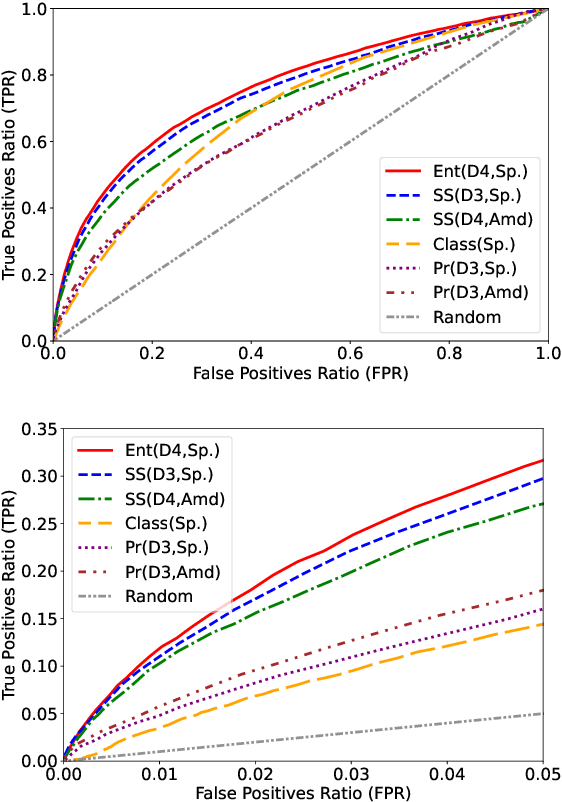
Studying Lobby Influence in the European Parliament

We present a method based on natural language processing (NLP), for studying the influence of interest groups (lobbies) in the law-making process in the European Parliament (EP). We collect and analyze novel datasets of lobbies' position papers and speeches made by members of the EP (MEPs). By comparing these texts on the basis of semantic similarity and entailment, we are able to discover interpretable links between MEPs and lobbies. In the absence of a ground-truth dataset of such links, we perform an indirect validation by comparing the discovered links with a dataset, which we curate, of retweet links between MEPs and lobbies, and with the publicly disclosed meetings of MEPs. Our best method achieves an AUC score of 0.77 and performs significantly better than several baselines. Moreover, an aggregate analysis of the discovered links, between groups of related lobbies and political groups of MEPs, correspond to the expectations from the ideology of the groups (e.g., center-left groups are associated with social causes). We believe that this work, which encompasses the methodology, datasets, and results, is a step towards enhancing the transparency of the intricate decision-making processes within democratic institutions.

It's All Relative: Interpretable Models for Scoring Bias in Documents

We propose an interpretable model to score the bias present in web documents, based only on their textual content. Our model incorporates assumptions reminiscent of the Bradley-Terry axioms and is trained on pairs of revisions of the same Wikipedia article, where one version is more biased than the other. While prior approaches based on absolute bias classification have struggled to obtain a high accuracy for the task, we are able to develop a useful model for scoring bias by learning to perform pairwise comparisons of bias accurately. We show that we can interpret the parameters of the trained model to discover the words most indicative of bias. We also apply our model in three different settings - studying the temporal evolution of bias in Wikipedia articles, comparing news sources based on bias, and scoring bias in law amendments. In each case, we demonstrate that the outputs of the model can be explained and validated, even for the two domains that are outside the training-data domain. We also use the model to compare the general level of bias between domains, where we see that legal texts are the least biased and news media are the most biased, with Wikipedia articles in between. Given its high performance, simplicity, interpretability, and wide applicability, we hope the model will be useful for a large community, including Wikipedia and news editors, political and social scientists, and the general public.

Fast Interactive Search with a Scale-Free Comparison Oracle

A comparison-based search algorithm lets a user find a target item $t$ in a database by answering queries of the form, ``Which of items $i$ and $j$ is closer to $t$?'' Instead of formulating an explicit query (such as one or several keywords), the user navigates towards the target via a sequence of such (typically noisy) queries. We propose a scale-free probabilistic oracle model called $\gamma$-CKL for such similarity triplets $(i,j;t)$, which generalizes the CKL triplet model proposed in the literature. The generalization affords independent control over the discriminating power of the oracle and the dimension of the feature space containing the items. We develop a search algorithm with provably exponential rate of convergence under the $\gamma$-CKL oracle, thanks to a backtracking strategy that deals with the unavoidable errors in updating the belief region around the target. We evaluate the performance of the algorithm both over the posited oracle and over several real-world triplet datasets. We also report on a comprehensive user study, where human subjects navigate a database of face portraits.