Optimal Graph Clustering without Edge Density Signals

This paper establishes the theoretical limits of graph clustering under the Popularity-Adjusted Block Model (PABM), addressing limitations of existing models. In contrast to the Stochastic Block Model (SBM), which assumes uniform vertex degrees, and to the Degree-Corrected Block Model (DCBM), which applies uniform degree corrections across clusters, PABM introduces separate popularity parameters for intra- and inter-cluster connections. Our main contribution is the characterization of the optimal error rate for clustering under PABM, which provides novel insights on clustering hardness: we demonstrate that unlike SBM and DCBM, cluster recovery remains possible in PABM even when traditional edge-density signals vanish, provided intra- and inter-cluster popularity coefficients differ. This highlights a dimension of degree heterogeneity captured by PABM but overlooked by DCBM: local differences in connectivity patterns can enhance cluster separability independently of global edge densities. Finally, because PABM exhibits a richer structure, its expected adjacency matrix has rank between $k$ and $k^2$, where $k$ is the number of clusters. As a result, spectral embeddings based on the top $k$ eigenvectors may fail to capture important structural information. Our numerical experiments on both synthetic and real datasets confirm that spectral clustering algorithms incorporating $k^2$ eigenvectors outperform traditional spectral approaches.

Why the Metric Backbone Preserves Community Structure

The metric backbone of a weighted graph is the union of all-pairs shortest paths. It is obtained by removing all edges $(u,v)$ that are not the shortest path between $u$ and $v$. In networks with well-separated communities, the metric backbone tends to preserve many inter-community edges, because these edges serve as bridges connecting two communities, but tends to delete many intra-community edges because the communities are dense. This suggests that the metric backbone would dilute or destroy the community structure of the network. However, this is not borne out by prior empirical work, which instead showed that the metric backbone of real networks preserves the community structure of the original network well. In this work, we analyze the metric backbone of a broad class of weighted random graphs with communities, and we formally prove the robustness of the community structure with respect to the deletion of all the edges that are not in the metric backbone. An empirical comparison of several graph sparsification techniques confirms our theoretical finding and shows that the metric backbone is an efficient sparsifier in the presence of communities.

Universal Lower Bounds and Optimal Rates: Achieving Minimax Clustering Error in Sub-Exponential Mixture Models

Clustering is a pivotal challenge in unsupervised machine learning and is often investigated through the lens of mixture models. The optimal error rate for recovering cluster labels in Gaussian and sub-Gaussian mixture models involves ad hoc signal-to-noise ratios. Simple iterative algorithms, such as Lloyd's algorithm, attain this optimal error rate. In this paper, we first establish a universal lower bound for the error rate in clustering any mixture model, expressed through a Chernoff divergence, a more versatile measure of model information than signal-to-noise ratios. We then demonstrate that iterative algorithms attain this lower bound in mixture models with sub-exponential tails, notably emphasizing location-scale mixtures featuring Laplace-distributed errors. Additionally, for datasets better modelled by Poisson or Negative Binomial mixtures, we study mixture models whose distributions belong to an exponential family. In such mixtures, we establish that Bregman hard clustering, a variant of Lloyd's algorithm employing a Bregman divergence, is rate optimal.

Exact Recovery and Bregman Hard Clustering of Node-Attributed Stochastic Block Model

Network clustering tackles the problem of identifying sets of nodes (communities) that have similar connection patterns. However, in many scenarios, nodes also have attributes that are correlated with the clustering structure. Thus, network information (edges) and node information (attributes) can be jointly leveraged to design high-performance clustering algorithms. Under a general model for the network and node attributes, this work establishes an information-theoretic criterion for the exact recovery of community labels and characterizes a phase transition determined by the Chernoff-Hellinger divergence of the model. The criterion shows how network and attribute information can be exchanged in order to have exact recovery (e.g., more reliable network information requires less reliable attribute information). This work also presents an iterative clustering algorithm that maximizes the joint likelihood, assuming that the probability distribution of network interactions and node attributes belong to exponential families. This covers a broad range of possible interactions (e.g., edges with weights) and attributes (e.g., non-Gaussian models), as well as sparse networks, while also exploring the connection between exponential families and Bregman divergences. Extensive numerical experiments using synthetic data indicate that the proposed algorithm outperforms classic algorithms that leverage only network or only attribute information as well as state-of-the-art algorithms that also leverage both sources of information. The contributions of this work provide insights into the fundamental limits and practical techniques for inferring community labels on node-attributed networks.

When Does Bottom-up Beat Top-down in Hierarchical Community Detection?

Hierarchical clustering of networks consists in finding a tree of communities, such that lower levels of the hierarchy reveal finer-grained community structures. There are two main classes of algorithms tackling this problem. Divisive ($\textit{top-down}$) algorithms recursively partition the nodes into two communities, until a stopping rule indicates that no further split is needed. In contrast, agglomerative ($\textit{bottom-up}$) algorithms first identify the smallest community structure and then repeatedly merge the communities using a $\textit{linkage}$ method. In this article, we establish theoretical guarantees for the recovery of the hierarchical tree and community structure of a Hierarchical Stochastic Block Model by a bottom-up algorithm. We also establish that this bottom-up algorithm attains the information-theoretic threshold for exact recovery at intermediate levels of the hierarchy. Notably, these recovery conditions are less restrictive compared to those existing for top-down algorithms. This shows that bottom-up algorithms extend the feasible region for achieving exact recovery at intermediate levels. Numerical experiments on both synthetic and real data sets confirm the superiority of bottom-up algorithms over top-down algorithms. We also observe that top-down algorithms can produce dendrograms with inversions. These findings contribute to a better understanding of hierarchical clustering techniques and their applications in network analysis.

Higher-Order Spectral Clustering for Geometric Graphs

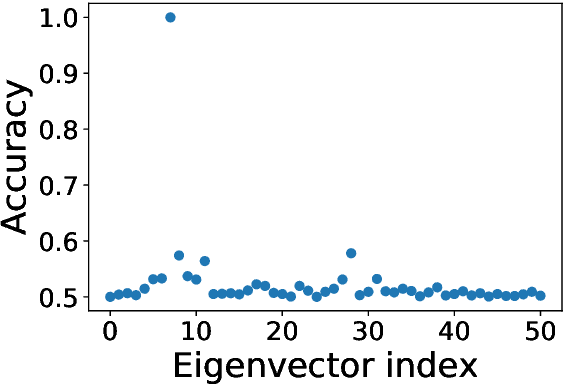
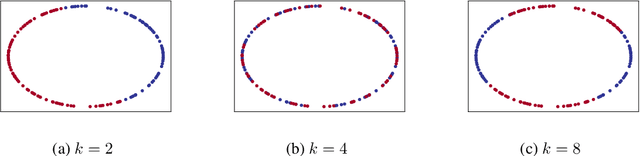
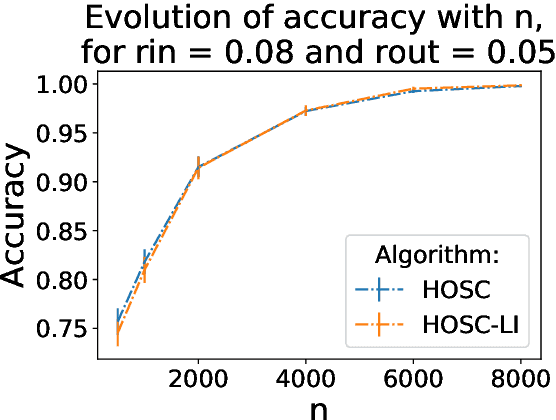
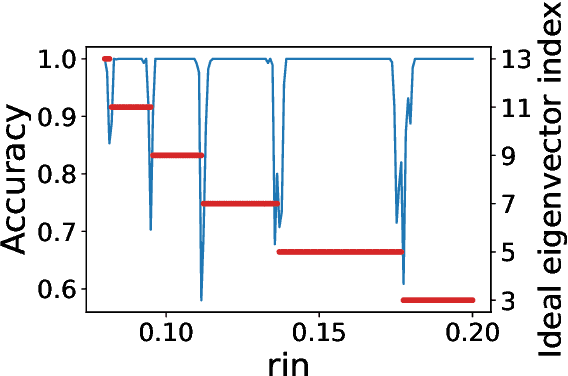
The present paper is devoted to clustering geometric graphs. While the standard spectral clustering is often not effective for geometric graphs, we present an effective generalization, which we call higher-order spectral clustering. It resembles in concept the classical spectral clustering method but uses for partitioning the eigenvector associated with a higher-order eigenvalue. We establish the weak consistency of this algorithm for a wide class of geometric graphs which we call Soft Geometric Block Model. A small adjustment of the algorithm provides strong consistency. We also show that our method is effective in numerical experiments even for graphs of modest size.

Estimation of Static Community Memberships from Temporal Network Data

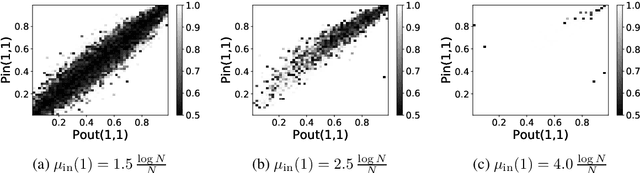
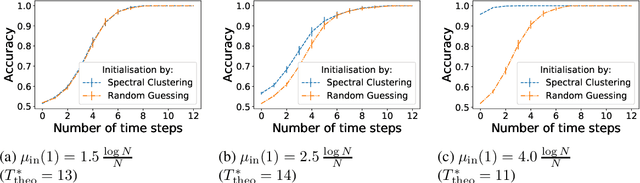
This article studies the estimation of static community memberships from temporally correlated pair interactions represented by an $N$-by-$N$-by-$T$ tensor where $N$ is the number of nodes and $T$ is the length of the time horizon. We present several estimation algorithms, both offline and online, which fully utilise the temporal nature of the observed data. As an information-theoretic benchmark, we study data sets generated by a dynamic stochastic block model, and derive fundamental information criteria for the recoverability of the community memberships as $N \to \infty$ both for bounded and diverging $T$. These results show that (i) even a small increase in $T$ may have a big impact on the recoverability of community memberships, (ii) consistent recovery is possible even for very sparse data (e.g. bounded average degree) when $T$ is large enough. We analyse the accuracy of the proposed estimation algorithms under various assumptions on data sparsity and identifiability, and prove that an efficient online algorithm is strongly consistent up to the information-theoretic threshold under suitable initialisation. Numerical experiments show that even a poor initial estimate (e.g., blind random guess) of the community assignment leads to high accuracy after a small number of iterations, and remarkably so also in very sparse regimes.

Almost exact recovery in noisy semi-supervised learning

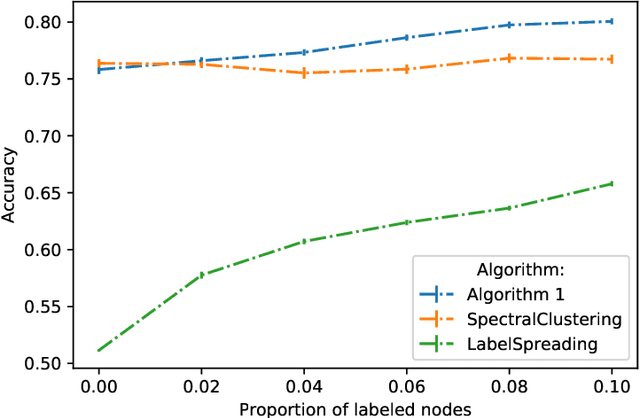
This paper investigates noisy graph-based semi-supervised learning or community detection. We consider the Stochastic Block Model (SBM), where, in addition to the graph observation, an oracle gives a non-perfect information about some nodes' cluster assignment. We derive the Maximum A Priori (MAP) estimator, and show that a continuous relaxation of the MAP performs almost exact recovery under non-restrictive conditions on the average degree and amount of oracle noise. In particular, this method avoids some pitfalls of several graph-based semi-supervised learning methods such as the flatness of the classification functions, appearing in the problems with a very large amount of unlabeled data.