Exact Recovery and Bregman Hard Clustering of Node-Attributed Stochastic Block Model

Network clustering tackles the problem of identifying sets of nodes (communities) that have similar connection patterns. However, in many scenarios, nodes also have attributes that are correlated with the clustering structure. Thus, network information (edges) and node information (attributes) can be jointly leveraged to design high-performance clustering algorithms. Under a general model for the network and node attributes, this work establishes an information-theoretic criterion for the exact recovery of community labels and characterizes a phase transition determined by the Chernoff-Hellinger divergence of the model. The criterion shows how network and attribute information can be exchanged in order to have exact recovery (e.g., more reliable network information requires less reliable attribute information). This work also presents an iterative clustering algorithm that maximizes the joint likelihood, assuming that the probability distribution of network interactions and node attributes belong to exponential families. This covers a broad range of possible interactions (e.g., edges with weights) and attributes (e.g., non-Gaussian models), as well as sparse networks, while also exploring the connection between exponential families and Bregman divergences. Extensive numerical experiments using synthetic data indicate that the proposed algorithm outperforms classic algorithms that leverage only network or only attribute information as well as state-of-the-art algorithms that also leverage both sources of information. The contributions of this work provide insights into the fundamental limits and practical techniques for inferring community labels on node-attributed networks.

struc2vec: Learning Node Representations from Structural Identity

Structural identity is a concept of symmetry in which network nodes are identified according to the network structure and their relationship to other nodes. Structural identity has been studied in theory and practice over the past decades, but only recently has it been addressed with representational learning techniques. This work presents struc2vec, a novel and flexible framework for learning latent representations for the structural identity of nodes. struc2vec uses a hierarchy to measure node similarity at different scales, and constructs a multilayer graph to encode structural similarities and generate structural context for nodes. Numerical experiments indicate that state-of-the-art techniques for learning node representations fail in capturing stronger notions of structural identity, while struc2vec exhibits much superior performance in this task, as it overcomes limitations of prior approaches. As a consequence, numerical experiments indicate that struc2vec improves performance on classification tasks that depend more on structural identity.

Learning Identity Mappings with Residual Gates

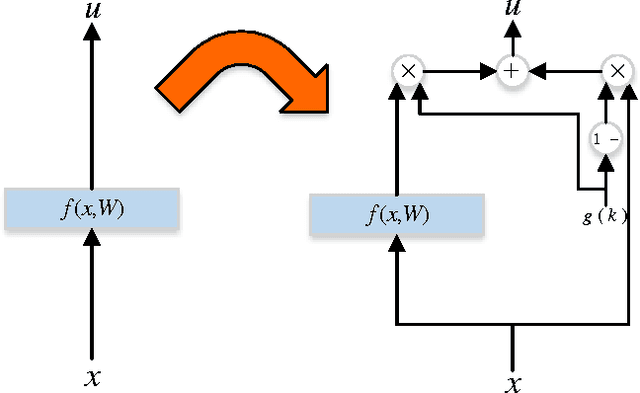
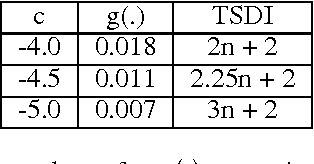
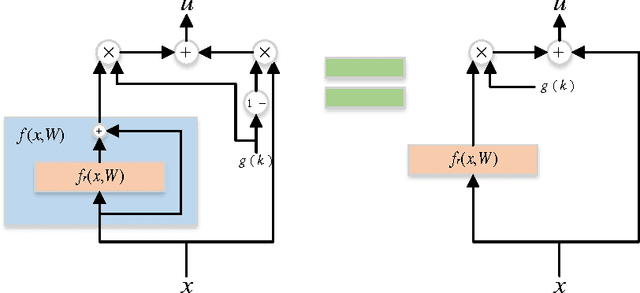
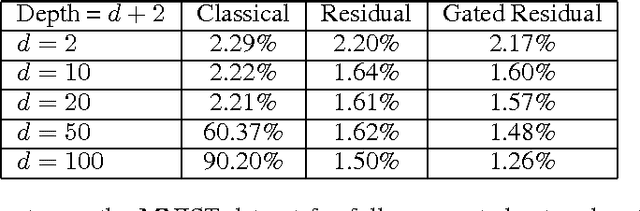
We propose a new layer design by adding a linear gating mechanism to shortcut connections. By using a scalar parameter to control each gate, we provide a way to learn identity mappings by optimizing only one parameter. We build upon the motivation behind Residual Networks, where a layer is reformulated in order to make learning identity mappings less problematic to the optimizer. The augmentation introduces only one extra parameter per layer, and provides easier optimization by making degeneration into identity mappings simpler. We propose a new model, the Gated Residual Network, which is the result when augmenting Residual Networks. Experimental results show that augmenting layers provides better optimization, increased performance, and more layer independence. We evaluate our method on MNIST using fully-connected networks, showing empirical indications that our augmentation facilitates the optimization of deep models, and that it provides high tolerance to full layer removal: the model retains over 90% of its performance even after half of its layers have been randomly removed. We also evaluate our model on CIFAR-10 and CIFAR-100 using Wide Gated ResNets, achieving 3.65% and 18.27% error, respectively.

On the Emergence of Shortest Paths by Reinforced Random Walks

The co-evolution between network structure and functional performance is a fundamental and challenging problem whose complexity emerges from the intrinsic interdependent nature of structure and function. Within this context, we investigate the interplay between the efficiency of network navigation (i.e., path lengths) and network structure (i.e., edge weights). We propose a simple and tractable model based on iterative biased random walks where edge weights increase over time as function of the traversed path length. Under mild assumptions, we prove that biased random walks will eventually only traverse shortest paths in their journey towards the destination. We further characterize the transient regime proving that the probability to traverse non-shortest paths decays according to a power-law. We also highlight various properties in this dynamic, such as the trade-off between exploration and convergence, and preservation of initial network plasticity. We believe the proposed model and results can be of interest to various domains where biased random walks and decentralized navigation have been applied.