Information Retrieval in the Age of Generative AI: The RGB Model

The advent of Large Language Models (LLMs) and generative AI is fundamentally transforming information retrieval and processing on the Internet, bringing both great potential and significant concerns regarding content authenticity and reliability. This paper presents a novel quantitative approach to shed light on the complex information dynamics arising from the growing use of generative AI tools. Despite their significant impact on the digital ecosystem, these dynamics remain largely uncharted and poorly understood. We propose a stochastic model to characterize the generation, indexing, and dissemination of information in response to new topics. This scenario particularly challenges current LLMs, which often rely on real-time Retrieval-Augmented Generation (RAG) techniques to overcome their static knowledge limitations. Our findings suggest that the rapid pace of generative AI adoption, combined with increasing user reliance, can outpace human verification, escalating the risk of inaccurate information proliferation across digital resources. An in-depth analysis of Stack Exchange data confirms that high-quality answers inevitably require substantial time and human effort to emerge. This underscores the considerable risks associated with generating persuasive text in response to new questions and highlights the critical need for responsible development and deployment of future generative AI tools.

Reconciling the Quality vs Popularity Dichotomy in Online Cultural Markets

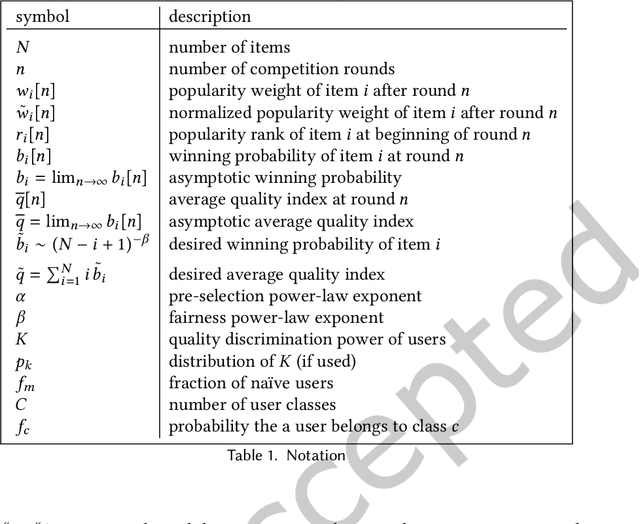
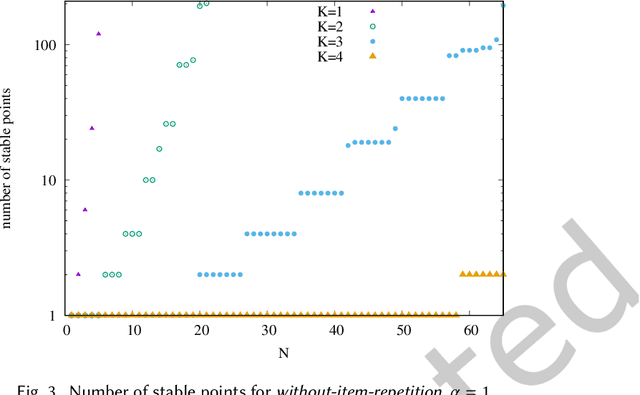
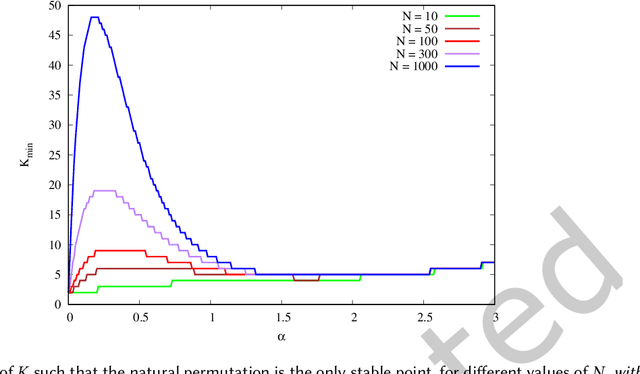
We propose a simple model of an idealized online cultural market in which $N$ items, endowed with a hidden quality metric, are recommended to users by a ranking algorithm possibly biased by the current items' popularity. Our goal is to better understand the underlying mechanisms of the well-known fact that popularity bias can prevent higher-quality items from becoming more popular than lower-quality items, producing an undesirable misalignment between quality and popularity rankings. We do so under the assumption that users, having limited time/attention, are able to discriminate the best-quality only within a random subset of the items. We discover the existence of a harmful regime in which improper use of popularity can seriously compromise the emergence of quality, and a benign regime in which wise use of popularity, coupled with a small discrimination effort on behalf of users, guarantees the perfect alignment of quality and popularity ranking. Our findings clarify the effects of algorithmic popularity bias on quality outcomes, and may inform the design of more principled mechanisms for techno-social cultural markets.

Content Placement in Networks of Similarity Caches

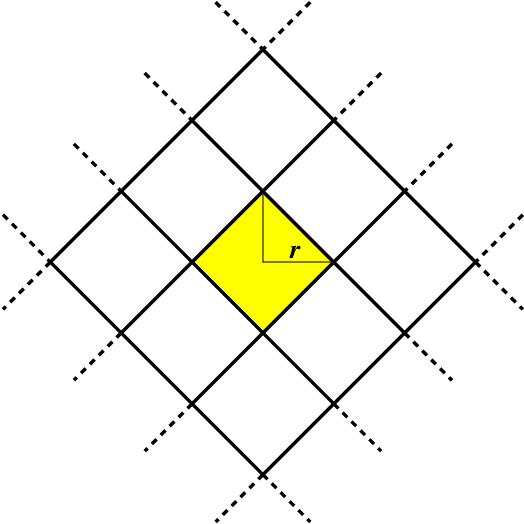
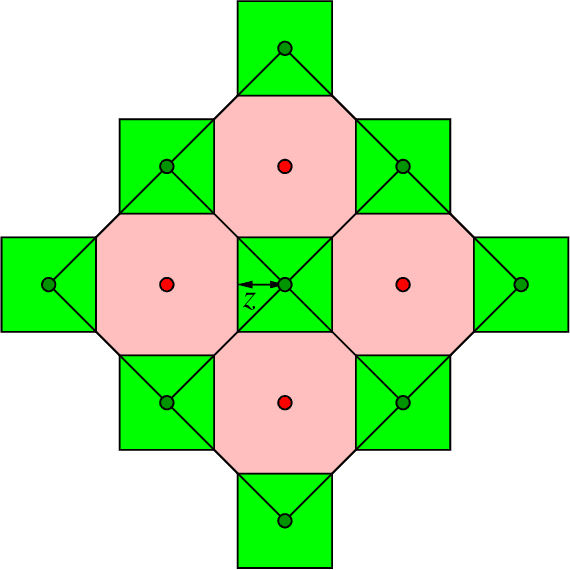
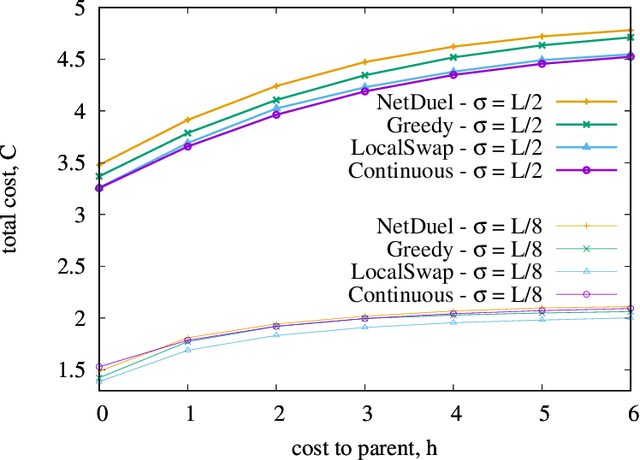
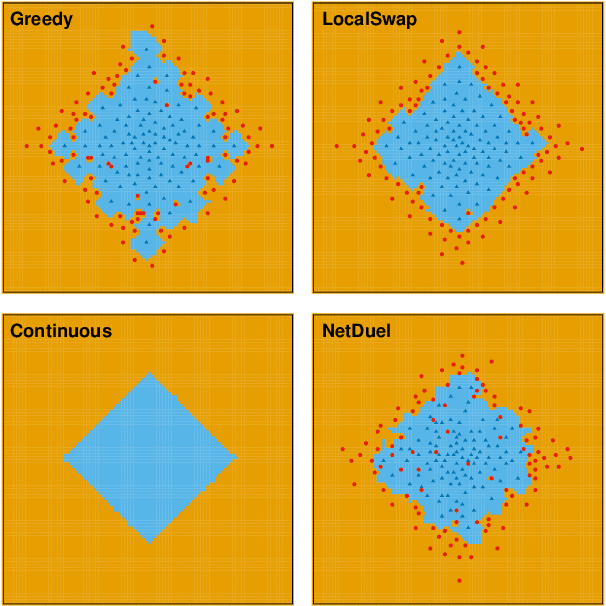
Similarity caching systems have recently attracted the attention of the scientific community, as they can be profitably used in many application contexts, like multimedia retrieval, advertising, object recognition, recommender systems and online content-match applications. In such systems, a user request for an object $o$, which is not in the cache, can be (partially) satisfied by a similar stored object $o$', at the cost of a loss of user utility. In this paper we make a first step into the novel area of similarity caching networks, where requests can be forwarded along a path of caches to get the best efficiency-accuracy tradeoff. The offline problem of content placement can be easily shown to be NP-hard, while different polynomial algorithms can be devised to approach the optimal solution in discrete cases. As the content space grows large, we propose a continuous problem formulation whose solution exhibits a simple structure in a class of tree topologies. We verify our findings using synthetic and realistic request traces.

On the Emergence of Shortest Paths by Reinforced Random Walks

The co-evolution between network structure and functional performance is a fundamental and challenging problem whose complexity emerges from the intrinsic interdependent nature of structure and function. Within this context, we investigate the interplay between the efficiency of network navigation (i.e., path lengths) and network structure (i.e., edge weights). We propose a simple and tractable model based on iterative biased random walks where edge weights increase over time as function of the traversed path length. Under mild assumptions, we prove that biased random walks will eventually only traverse shortest paths in their journey towards the destination. We further characterize the transient regime proving that the probability to traverse non-shortest paths decays according to a power-law. We also highlight various properties in this dynamic, such as the trade-off between exploration and convergence, and preservation of initial network plasticity. We believe the proposed model and results can be of interest to various domains where biased random walks and decentralized navigation have been applied.