Scalable Decentralized Algorithms for Online Personalized Mean Estimation

In numerous settings, agents lack sufficient data to directly learn a model. Collaborating with other agents may help, but it introduces a bias-variance trade-off, when local data distributions differ. A key challenge is for each agent to identify clients with similar distributions while learning the model, a problem that remains largely unresolved. This study focuses on a simplified version of the overarching problem, where each agent collects samples from a real-valued distribution over time to estimate its mean. Existing algorithms face impractical space and time complexities (quadratic in the number of agents A). To address scalability challenges, we propose a framework where agents self-organize into a graph, allowing each agent to communicate with only a selected number of peers r. We introduce two collaborative mean estimation algorithms: one draws inspiration from belief propagation, while the other employs a consensus-based approach, with complexity of O( r |A| log |A|) and O(r |A|), respectively. We establish conditions under which both algorithms yield asymptotically optimal estimates and offer a theoretical characterization of their performance.

Ranking a Set of Objects using Heterogeneous Workers: QUITE an Easy Problem

We focus on the problem of ranking $N$ objects starting from a set of noisy pairwise comparisons provided by a crowd of unequal workers, each worker being characterized by a specific degree of reliability, which reflects her ability to rank pairs of objects. More specifically, we assume that objects are endowed with intrinsic qualities and that the probability with which an object is preferred to another depends both on the difference between the qualities of the two competitors and on the reliability of the worker. We propose QUITE, a non-adaptive ranking algorithm that jointly estimates workers' reliabilities and qualities of objects. Performance of QUITE is compared in different scenarios against previously proposed algorithms. Finally, we show how QUITE can be naturally made adaptive.

Federated Learning under Heterogeneous and Correlated Client Availability

The enormous amount of data produced by mobile and IoT devices has motivated the development of federated learning (FL), a framework allowing such devices (or clients) to collaboratively train machine learning models without sharing their local data. FL algorithms (like FedAvg) iteratively aggregate model updates computed by clients on their own datasets. Clients may exhibit different levels of participation, often correlated over time and with other clients. This paper presents the first convergence analysis for a FedAvg-like FL algorithm under heterogeneous and correlated client availability. Our analysis highlights how correlation adversely affects the algorithm's convergence rate and how the aggregation strategy can alleviate this effect at the cost of steering training toward a biased model. Guided by the theoretical analysis, we propose CA-Fed, a new FL algorithm that tries to balance the conflicting goals of maximizing convergence speed and minimizing model bias. To this purpose, CA-Fed dynamically adapts the weight given to each client and may ignore clients with low availability and large correlation. Our experimental results show that CA-Fed achieves higher time-average accuracy and a lower standard deviation than state-of-the-art AdaFed and F3AST, both on synthetic and real datasets.

Content Placement in Networks of Similarity Caches

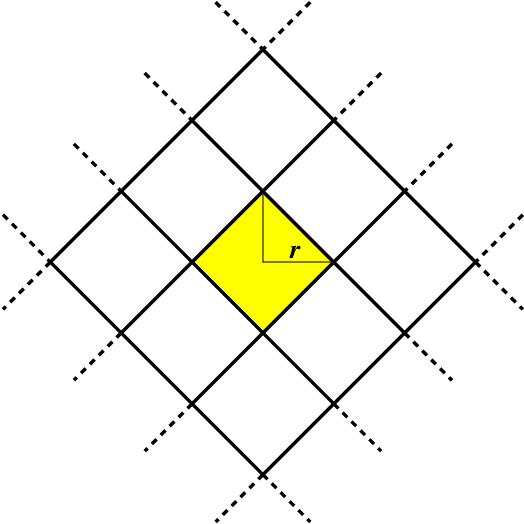
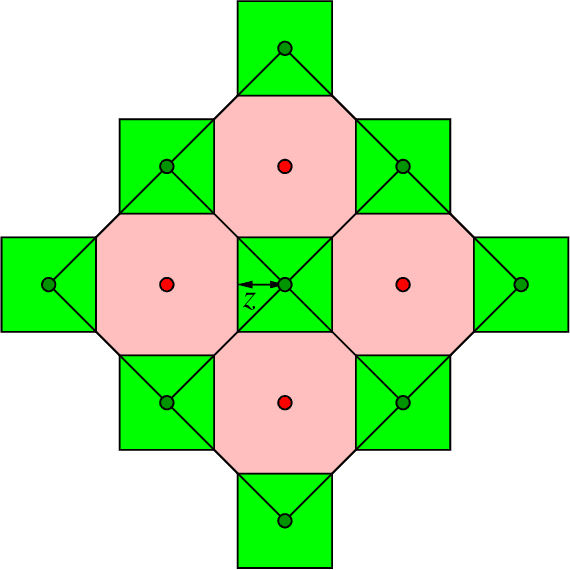
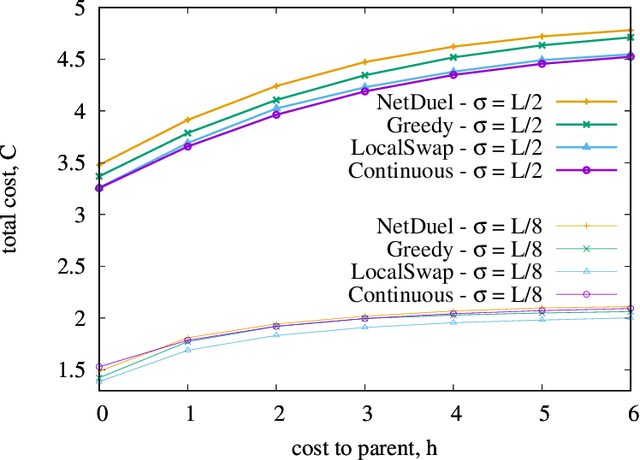
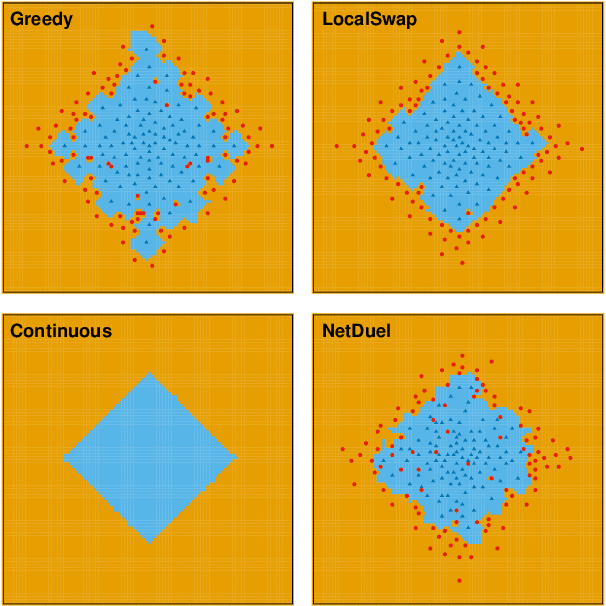
Similarity caching systems have recently attracted the attention of the scientific community, as they can be profitably used in many application contexts, like multimedia retrieval, advertising, object recognition, recommender systems and online content-match applications. In such systems, a user request for an object $o$, which is not in the cache, can be (partially) satisfied by a similar stored object $o$', at the cost of a loss of user utility. In this paper we make a first step into the novel area of similarity caching networks, where requests can be forwarded along a path of caches to get the best efficiency-accuracy tradeoff. The offline problem of content placement can be easily shown to be NP-hard, while different polynomial algorithms can be devised to approach the optimal solution in discrete cases. As the content space grows large, we propose a continuous problem formulation whose solution exhibits a simple structure in a class of tree topologies. We verify our findings using synthetic and realistic request traces.

Ranking a set of objects: a graph based least-square approach

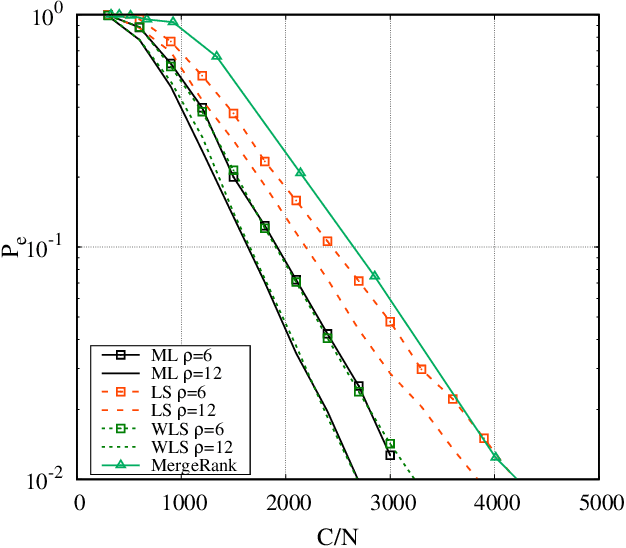
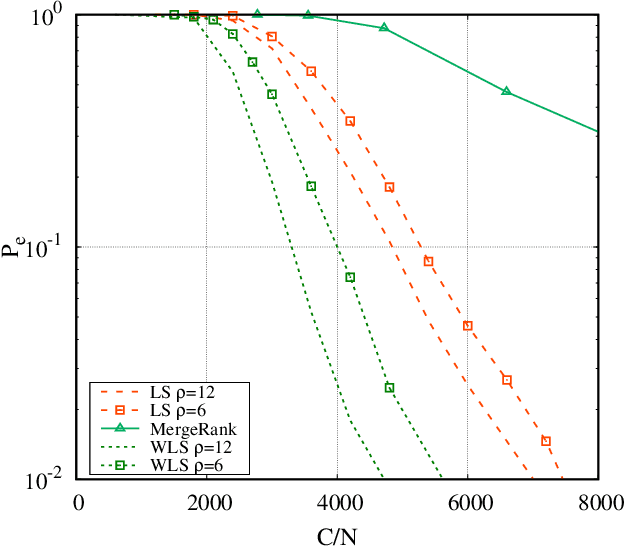
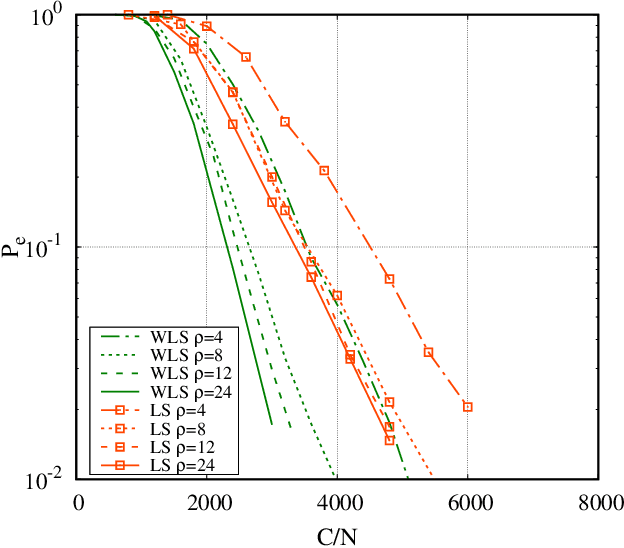
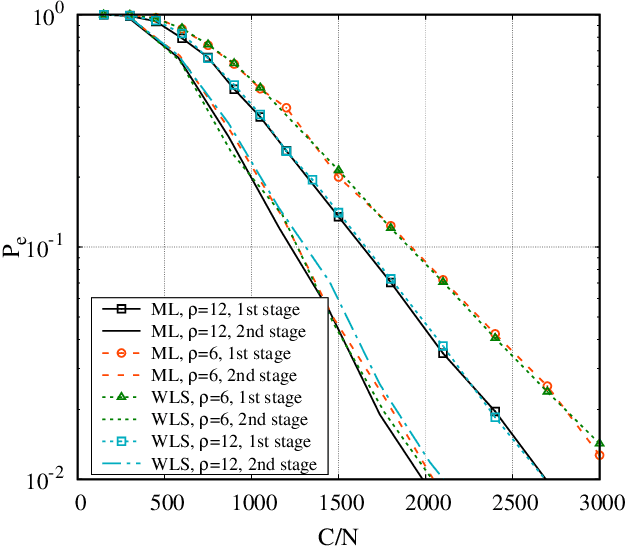
We consider the problem of ranking $N$ objects starting from a set of noisy pairwise comparisons provided by a crowd of equal workers. We assume that objects are endowed with intrinsic qualities and that the probability with which an object is preferred to another depends only on the difference between the qualities of the two competitors. We propose a class of non-adaptive ranking algorithms that rely on a least-squares optimization criterion for the estimation of qualities. Such algorithms are shown to be asymptotically optimal (i.e., they require $O(\frac{N}{\epsilon^2}\log \frac{N}{\delta})$ comparisons to be $(\epsilon, \delta)$-PAC). Numerical results show that our schemes are very efficient also in many non-asymptotic scenarios exhibiting a performance similar to the maximum-likelihood algorithm. Moreover, we show how they can be extended to adaptive schemes and test them on real-world datasets.

Selecting the top-quality item through crowd scoring

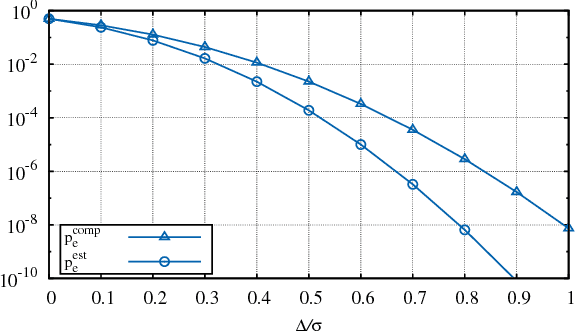
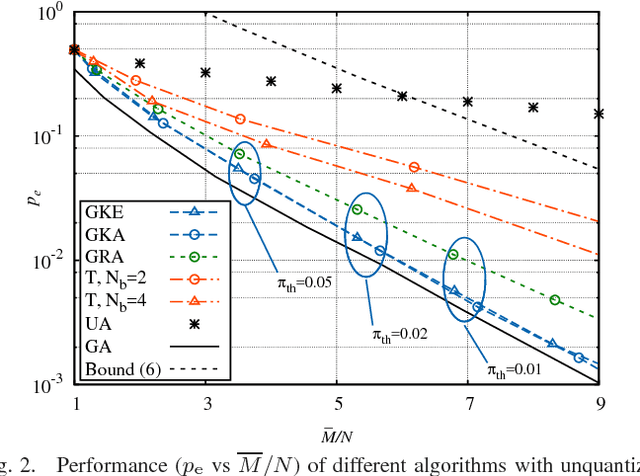
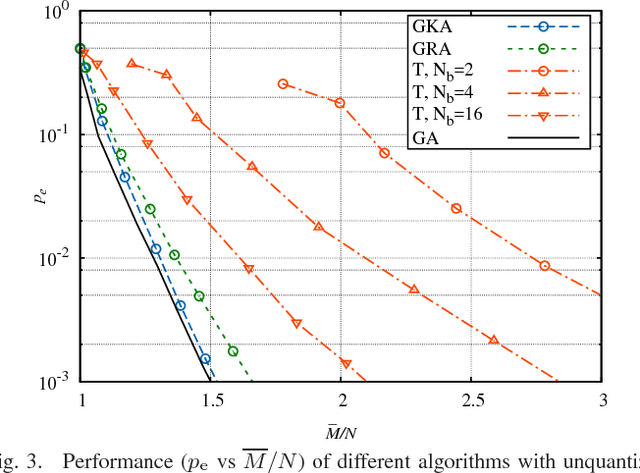
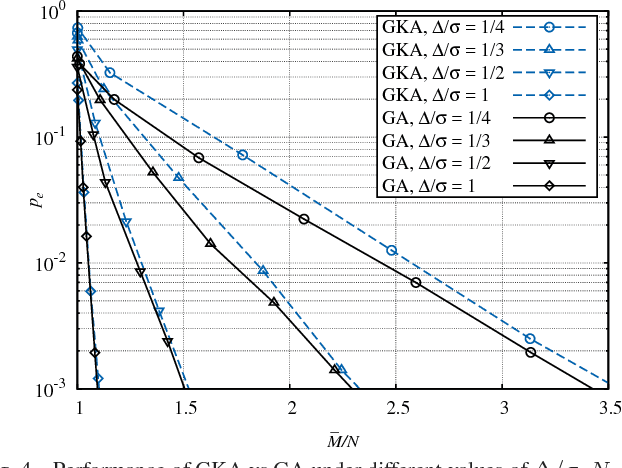
We investigate crowdsourcing algorithms for finding the top-quality item within a large collection of objects with unknown intrinsic quality values. This is an important problem with many relevant applications, for example in networked recommendation systems. The core of the algorithms is that objects are distributed to crowd workers, who return a noisy and biased evaluation. All received evaluations are then combined, to identify the top-quality object. We first present a simple probabilistic model for the system under investigation. Then, we devise and study a class of efficient adaptive algorithms to assign in an effective way objects to workers. We compare the performance of several algorithms, which correspond to different choices of the design parameters/metrics. In the simulations we show that some of the algorithms achieve near optimal performance for a suitable setting of the system parameters.