Estimation of Static Community Memberships from Temporal Network Data
Paper and Code
Aug 12, 2020

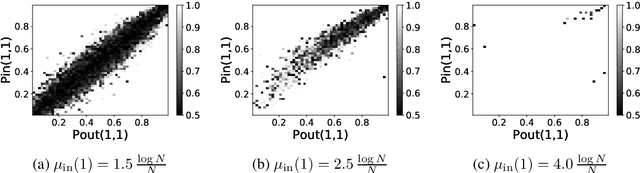
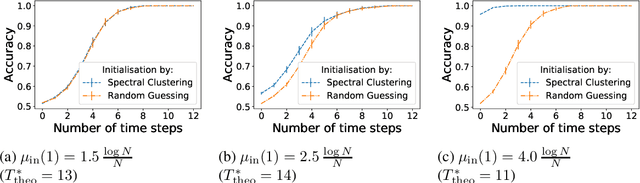
This article studies the estimation of static community memberships from temporally correlated pair interactions represented by an $N$-by-$N$-by-$T$ tensor where $N$ is the number of nodes and $T$ is the length of the time horizon. We present several estimation algorithms, both offline and online, which fully utilise the temporal nature of the observed data. As an information-theoretic benchmark, we study data sets generated by a dynamic stochastic block model, and derive fundamental information criteria for the recoverability of the community memberships as $N \to \infty$ both for bounded and diverging $T$. These results show that (i) even a small increase in $T$ may have a big impact on the recoverability of community memberships, (ii) consistent recovery is possible even for very sparse data (e.g. bounded average degree) when $T$ is large enough. We analyse the accuracy of the proposed estimation algorithms under various assumptions on data sparsity and identifiability, and prove that an efficient online algorithm is strongly consistent up to the information-theoretic threshold under suitable initialisation. Numerical experiments show that even a poor initial estimate (e.g., blind random guess) of the community assignment leads to high accuracy after a small number of iterations, and remarkably so also in very sparse regimes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge