Lagrangian Index Policy for Restless Bandits with Average Reward

We study the Lagrangian Index Policy (LIP) for restless multi-armed bandits with long-run average reward. In particular, we compare the performance of LIP with the performance of the Whittle Index Policy (WIP), both heuristic policies known to be asymptotically optimal under certain natural conditions. Even though in most cases their performances are very similar, in the cases when WIP shows bad performance, LIP continues to perform very well. We then propose reinforcement learning algorithms, both tabular and NN-based, to obtain online learning schemes for LIP in the model-free setting. The proposed reinforcement learning schemes for LIP requires significantly less memory than the analogous scheme for WIP. We calculate analytically the Lagrangian index for the restart model, which describes the optimal web crawling and the minimization of the weighted age of information. We also give a new proof of asymptotic optimality in case of homogeneous bandits as the number of arms goes to infinity, based on exchangeability and de Finetti's theorem.

Tabular and Deep Learning for the Whittle Index

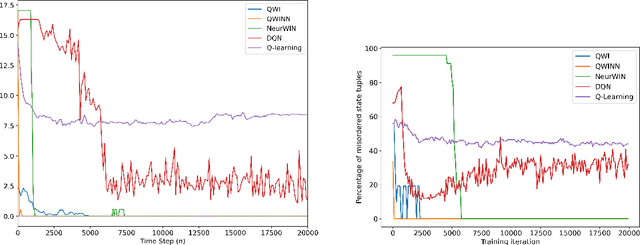
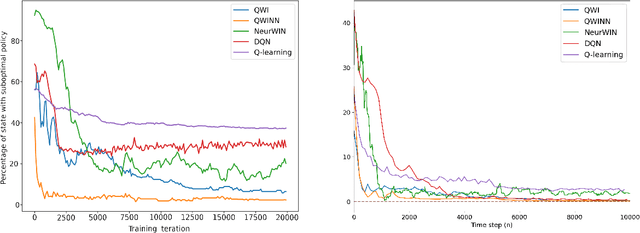
The Whittle index policy is a heuristic that has shown remarkably good performance (with guaranteed asymptotic optimality) when applied to the class of problems known as Restless Multi-Armed Bandit Problems (RMABPs). In this paper we present QWI and QWINN, two reinforcement learning algorithms, respectively tabular and deep, to learn the Whittle index for the total discounted criterion. The key feature is the use of two time-scales, a faster one to update the state-action Q -values, and a relatively slower one to update the Whittle indices. In our main theoretical result we show that QWI, which is a tabular implementation, converges to the real Whittle indices. We then present QWINN, an adaptation of QWI algorithm using neural networks to compute the Q -values on the faster time-scale, which is able to extrapolate information from one state to another and scales naturally to large state-space environments. For QWINN, we show that all local minima of the Bellman error are locally stable equilibria, which is the first result of its kind for DQN-based schemes. Numerical computations show that QWI and QWINN converge faster than the standard Q -learning algorithm, neural-network based approximate Q-learning and other state of the art algorithms.

Deep reinforcement learning for weakly coupled MDP's with continuous actions

This paper introduces the Lagrange Policy for Continuous Actions (LPCA), a reinforcement learning algorithm specifically designed for weakly coupled MDP problems with continuous action spaces. LPCA addresses the challenge of resource constraints dependent on continuous actions by introducing a Lagrange relaxation of the weakly coupled MDP problem within a neural network framework for Q-value computation. This approach effectively decouples the MDP, enabling efficient policy learning in resource-constrained environments. We present two variations of LPCA: LPCA-DE, which utilizes differential evolution for global optimization, and LPCA-Greedy, a method that incrementally and greadily selects actions based on Q-value gradients. Comparative analysis against other state-of-the-art techniques across various settings highlight LPCA's robustness and efficiency in managing resource allocation while maximizing rewards.

Full Gradient Deep Reinforcement Learning for Average-Reward Criterion

We extend the provably convergent Full Gradient DQN algorithm for discounted reward Markov decision processes from Avrachenkov et al. (2021) to average reward problems. We experimentally compare widely used RVI Q-Learning with recently proposed Differential Q-Learning in the neural function approximation setting with Full Gradient DQN and DQN. We also extend this to learn Whittle indices for Markovian restless multi-armed bandits. We observe a better convergence rate of the proposed Full Gradient variant across different tasks.

Multilayer hypergraph clustering using the aggregate similarity matrix

We consider the community recovery problem on a multilayer variant of the hypergraph stochastic block model (HSBM). Each layer is associated with an independent realization of a d-uniform HSBM on N vertices. Given the aggregated number of hyperedges incident to each pair of vertices, represented using a similarity matrix, the goal is to obtain a partition of the N vertices into disjoint communities. In this work, we investigate a semidefinite programming (SDP) approach and obtain information-theoretic conditions on the model parameters that guarantee exact recovery both in the assortative and the disassortative cases.

Higher-Order Spectral Clustering for Geometric Graphs

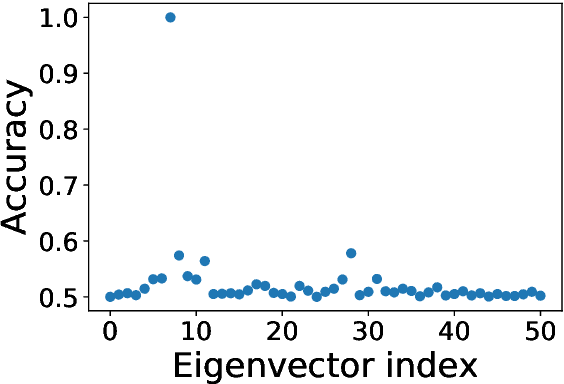
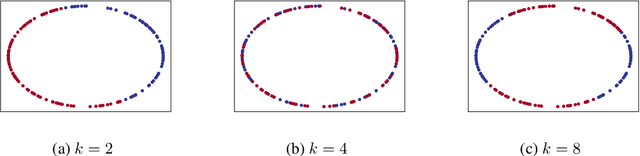
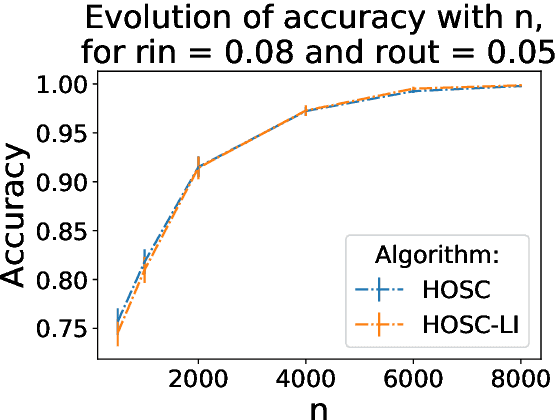
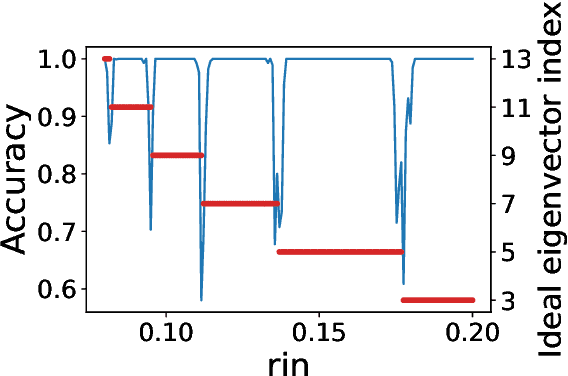
The present paper is devoted to clustering geometric graphs. While the standard spectral clustering is often not effective for geometric graphs, we present an effective generalization, which we call higher-order spectral clustering. It resembles in concept the classical spectral clustering method but uses for partitioning the eigenvector associated with a higher-order eigenvalue. We establish the weak consistency of this algorithm for a wide class of geometric graphs which we call Soft Geometric Block Model. A small adjustment of the algorithm provides strong consistency. We also show that our method is effective in numerical experiments even for graphs of modest size.

Online Algorithms for Estimating Change Rates of Web Pages

For providing quick and accurate search results, a search engine maintains a local snapshot of the entire web. And, to keep this local cache fresh, it employs a crawler for tracking changes across various web pages. It would have been ideal if the crawler managed to update the local snapshot as soon as a page changed on the web. However, finite bandwidth availability and server restrictions mean that there is a bound on how frequently the different pages can be crawled. This then brings forth the following optimisation problem: maximise the freshness of the local cache subject to the crawling frequency being within the prescribed bounds. Recently, tractable algorithms have been proposed to solve this optimisation problem under different cost criteria. However, these assume the knowledge of exact page change rates, which is unrealistic in practice. We address this issue here. Specifically, we provide three novel schemes for online estimation of page change rates. All these schemes only need partial information about the page change process, i.e., they only need to know if the page has changed or not since the last crawl instance. Our first scheme is based on the law of large numbers, the second on the theory of stochastic approximation, while the third is an extension of the second and involves an additional momentum term. For all of these schemes, we prove convergence and, also, provide their convergence rates. As far as we know, the results concerning the third estimator is quite novel. Specifically, this is the first convergence type result for a stochastic approximation algorithm with momentum. Finally, we provide some numerical experiments (on real as well as synthetic data) to compare the performance of our proposed estimators with the existing ones (e.g., MLE).

LFGCN: Levitating over Graphs with Levy Flights

Due to high utility in many applications, from social networks to blockchain to power grids, deep learning on non-Euclidean objects such as graphs and manifolds, coined Geometric Deep Learning (GDL), continues to gain an ever increasing interest. We propose a new L\'evy Flights Graph Convolutional Networks (LFGCN) method for semi-supervised learning, which casts the L\'evy Flights into random walks on graphs and, as a result, allows both to accurately account for the intrinsic graph topology and to substantially improve classification performance, especially for heterogeneous graphs. Furthermore, we propose a new preferential P-DropEdge method based on the Girvan-Newman argument. That is, in contrast to uniform removing of edges as in DropEdge, following the Girvan-Newman algorithm, we detect network periphery structures using information on edge betweenness and then remove edges according to their betweenness centrality. Our experimental results on semi-supervised node classification tasks demonstrate that the LFGCN coupled with P-DropEdge accelerates the training task, increases stability and further improves predictive accuracy of learned graph topology structure. Finally, in our case studies we bring the machinery of LFGCN and other deep networks tools to analysis of power grid networks - the area where the utility of GDL remains untapped.

Estimation of Static Community Memberships from Temporal Network Data

This article studies the estimation of static community memberships from temporally correlated pair interactions represented by an $N$-by-$N$-by-$T$ tensor where $N$ is the number of nodes and $T$ is the length of the time horizon. We present several estimation algorithms, both offline and online, which fully utilise the temporal nature of the observed data. As an information-theoretic benchmark, we study data sets generated by a dynamic stochastic block model, and derive fundamental information criteria for the recoverability of the community memberships as $N \to \infty$ both for bounded and diverging $T$. These results show that (i) even a small increase in $T$ may have a big impact on the recoverability of community memberships, (ii) consistent recovery is possible even for very sparse data (e.g. bounded average degree) when $T$ is large enough. We analyse the accuracy of the proposed estimation algorithms under various assumptions on data sparsity and identifiability, and prove that an efficient online algorithm is strongly consistent up to the information-theoretic threshold under suitable initialisation. Numerical experiments show that even a poor initial estimate (e.g., blind random guess) of the community assignment leads to high accuracy after a small number of iterations, and remarkably so also in very sparse regimes.

Almost exact recovery in noisy semi-supervised learning

This paper investigates noisy graph-based semi-supervised learning or community detection. We consider the Stochastic Block Model (SBM), where, in addition to the graph observation, an oracle gives a non-perfect information about some nodes' cluster assignment. We derive the Maximum A Priori (MAP) estimator, and show that a continuous relaxation of the MAP performs almost exact recovery under non-restrictive conditions on the average degree and amount of oracle noise. In particular, this method avoids some pitfalls of several graph-based semi-supervised learning methods such as the flatness of the classification functions, appearing in the problems with a very large amount of unlabeled data.