Tabular and Deep Learning for the Whittle Index

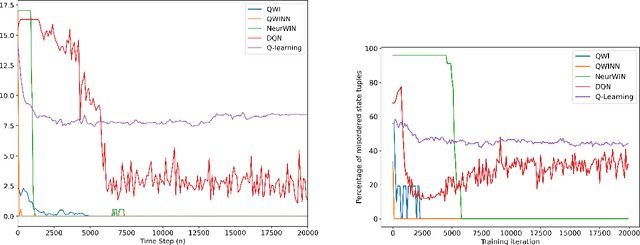
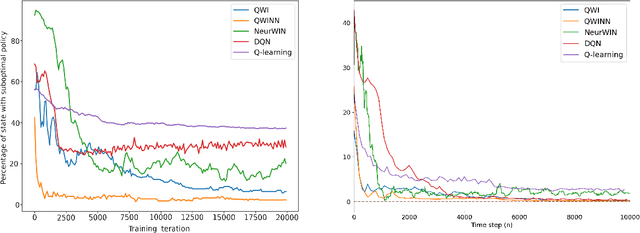
The Whittle index policy is a heuristic that has shown remarkably good performance (with guaranteed asymptotic optimality) when applied to the class of problems known as Restless Multi-Armed Bandit Problems (RMABPs). In this paper we present QWI and QWINN, two reinforcement learning algorithms, respectively tabular and deep, to learn the Whittle index for the total discounted criterion. The key feature is the use of two time-scales, a faster one to update the state-action Q -values, and a relatively slower one to update the Whittle indices. In our main theoretical result we show that QWI, which is a tabular implementation, converges to the real Whittle indices. We then present QWINN, an adaptation of QWI algorithm using neural networks to compute the Q -values on the faster time-scale, which is able to extrapolate information from one state to another and scales naturally to large state-space environments. For QWINN, we show that all local minima of the Bellman error are locally stable equilibria, which is the first result of its kind for DQN-based schemes. Numerical computations show that QWI and QWINN converge faster than the standard Q -learning algorithm, neural-network based approximate Q-learning and other state of the art algorithms.

Deep reinforcement learning for weakly coupled MDP's with continuous actions

This paper introduces the Lagrange Policy for Continuous Actions (LPCA), a reinforcement learning algorithm specifically designed for weakly coupled MDP problems with continuous action spaces. LPCA addresses the challenge of resource constraints dependent on continuous actions by introducing a Lagrange relaxation of the weakly coupled MDP problem within a neural network framework for Q-value computation. This approach effectively decouples the MDP, enabling efficient policy learning in resource-constrained environments. We present two variations of LPCA: LPCA-DE, which utilizes differential evolution for global optimization, and LPCA-Greedy, a method that incrementally and greadily selects actions based on Q-value gradients. Comparative analysis against other state-of-the-art techniques across various settings highlight LPCA's robustness and efficiency in managing resource allocation while maximizing rewards.