Tabular and Deep Learning for the Whittle Index

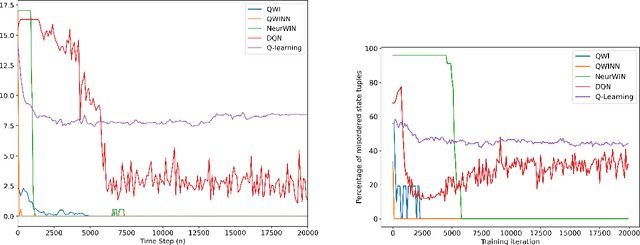
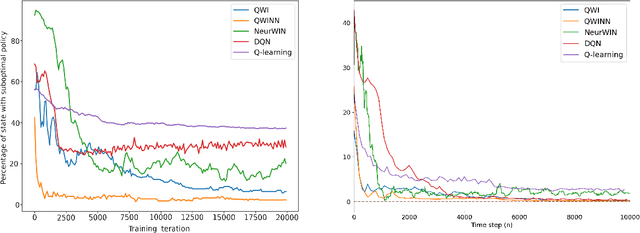
The Whittle index policy is a heuristic that has shown remarkably good performance (with guaranteed asymptotic optimality) when applied to the class of problems known as Restless Multi-Armed Bandit Problems (RMABPs). In this paper we present QWI and QWINN, two reinforcement learning algorithms, respectively tabular and deep, to learn the Whittle index for the total discounted criterion. The key feature is the use of two time-scales, a faster one to update the state-action Q -values, and a relatively slower one to update the Whittle indices. In our main theoretical result we show that QWI, which is a tabular implementation, converges to the real Whittle indices. We then present QWINN, an adaptation of QWI algorithm using neural networks to compute the Q -values on the faster time-scale, which is able to extrapolate information from one state to another and scales naturally to large state-space environments. For QWINN, we show that all local minima of the Bellman error are locally stable equilibria, which is the first result of its kind for DQN-based schemes. Numerical computations show that QWI and QWINN converge faster than the standard Q -learning algorithm, neural-network based approximate Q-learning and other state of the art algorithms.

Full Gradient Deep Reinforcement Learning for Average-Reward Criterion

We extend the provably convergent Full Gradient DQN algorithm for discounted reward Markov decision processes from Avrachenkov et al. (2021) to average reward problems. We experimentally compare widely used RVI Q-Learning with recently proposed Differential Q-Learning in the neural function approximation setting with Full Gradient DQN and DQN. We also extend this to learn Whittle indices for Markovian restless multi-armed bandits. We observe a better convergence rate of the proposed Full Gradient variant across different tasks.

A Concentration Bound for Distributed Stochastic Approximation

We revisit the classical model of Tsitsiklis, Bertsekas and Athans for distributed stochastic approximation with consensus. The main result is an analysis of this scheme using the ODE approach to stochastic approximation, leading to a high probability bound for the tracking error between suitably interpolated iterates and the limiting differential equation. Several future directions will also be highlighted.

Concentration bounds for SSP Q-learning for average cost MDPs

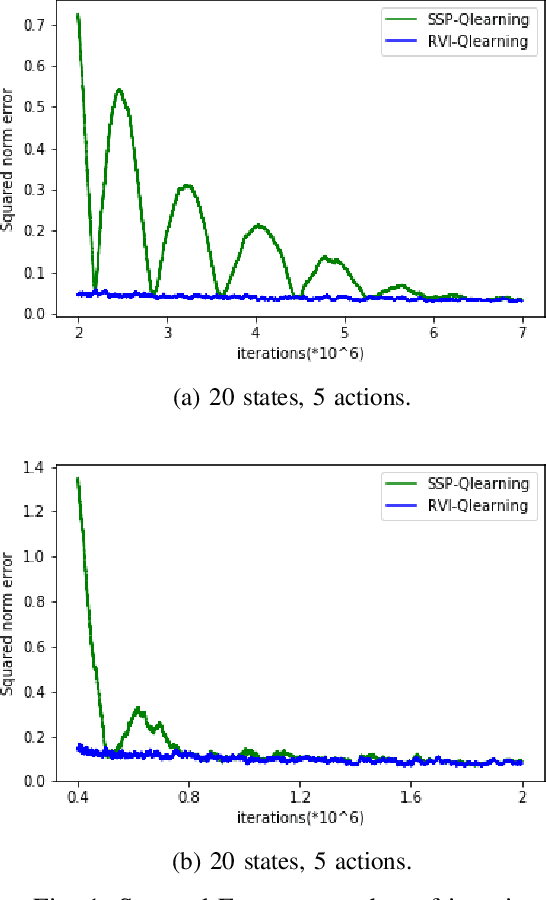
We derive a concentration bound for a Q-learning algorithm for average cost Markov decision processes based on an equivalent shortest path problem, and compare it numerically with the alternative scheme based on relative value iteration.

The ODE Method for Asymptotic Statistics in Stochastic Approximation and Reinforcement Learning

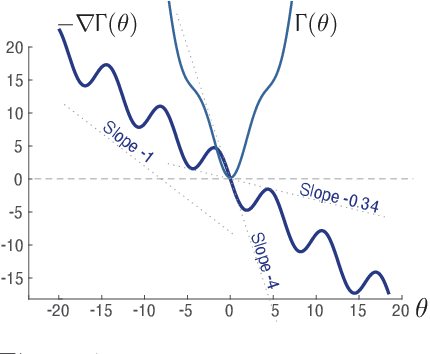
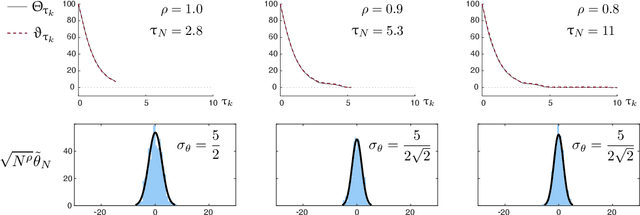
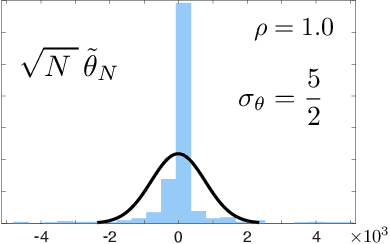
The paper concerns convergence and asymptotic statistics for stochastic approximation driven by Markovian noise: $$ \theta_{n+1}= \theta_n + \alpha_{n + 1} f(\theta_n, \Phi_{n+1}) \,,\quad n\ge 0, $$ in which each $\theta_n\in\Re^d$, $ \{ \Phi_n \}$ is a Markov chain on a general state space X with stationary distribution $\pi$, and $f:\Re^d\times \text{X} \to\Re^d$. In addition to standard Lipschitz bounds on $f$, and conditions on the vanishing step-size sequence $\{\alpha_n\}$, it is assumed that the associated ODE is globally asymptotically stable with stationary point denoted $\theta^*$, where $\bar f(\theta)=E[f(\theta,\Phi)]$ with $\Phi\sim\pi$. Moreover, the ODE@$\infty$ defined with respect to the vector field, $$ \bar f_\infty(\theta):= \lim_{r\to\infty} r^{-1} \bar f(r\theta) \,,\qquad \theta\in\Re^d, $$ is asymptotically stable. The main contributions are summarized as follows: (i) The sequence $\theta$ is convergent if $\Phi$ is geometrically ergodic, and subject to compatible bounds on $f$. The remaining results are established under a stronger assumption on the Markov chain: A slightly weaker version of the Donsker-Varadhan Lyapunov drift condition known as (DV3). (ii) A Lyapunov function is constructed for the joint process $\{\theta_n,\Phi_n\}$ that implies convergence of $\{ \theta_n\}$ in $L_4$. (iii) A functional CLT is established, as well as the usual one-dimensional CLT for the normalized error $z_n:= (\theta_n-\theta^*)/\sqrt{\alpha_n}$. Moment bounds combined with the CLT imply convergence of the normalized covariance, $$ \lim_{n \to \infty} E [ z_n z_n^T ] = \Sigma_\theta, $$ where $\Sigma_\theta$ is the asymptotic covariance appearing in the CLT. (iv) An example is provided where the Markov chain $\Phi$ is geometrically ergodic but it does not satisfy (DV3). While the algorithm is convergent, the second moment is unbounded.

Maximizing Conditional Entropy for Batch-Mode Active Learning of Perceptual Metrics

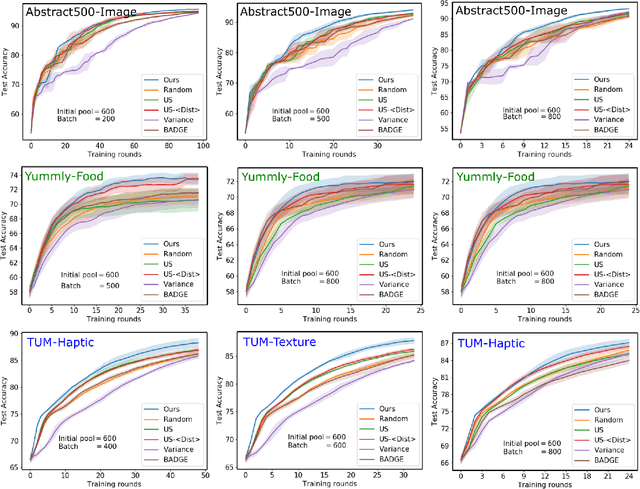
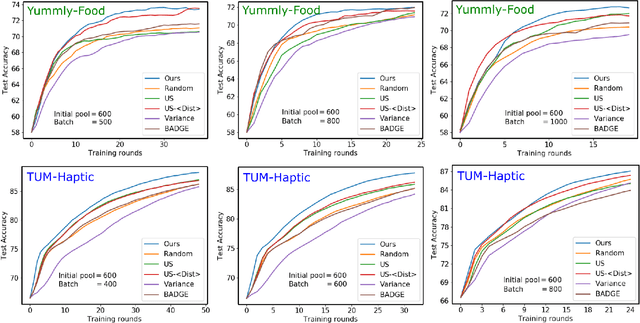
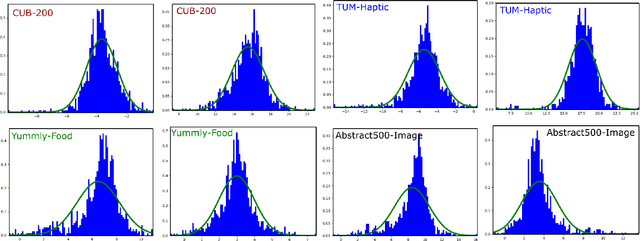
Active metric learning is the problem of incrementally selecting batches of training data (typically, ordered triplets) to annotate, in order to progressively improve a learned model of a metric over some input domain as rapidly as possible. Standard approaches, which independently select each triplet in a batch, are susceptible to highly correlated batches with many redundant triplets and hence low overall utility. While there has been recent work on selecting decorrelated batches for metric learning \cite{kumari2020batch}, these methods rely on ad hoc heuristics to estimate the correlation between two triplets at a time. We present a novel approach for batch mode active metric learning using the Maximum Entropy Principle that seeks to collectively select batches with maximum joint entropy, which captures both the informativeness and the diversity of the triplets. The entropy is derived from the second-order statistics estimated by dropout. We take advantage of the monotonically increasing submodular entropy function to construct an efficient greedy algorithm based on Gram-Schmidt orthogonalization that is provably $\left( 1 - \frac{1}{e} \right)$-optimal. Our approach is the first batch-mode active metric learning method to define a unified score that balances informativeness and diversity for an entire batch of triplets. Experiments with several real-world datasets demonstrate that our algorithm is robust and consistently outperforms the state-of-the-art.

Online Reinforcement Learning of Optimal Threshold Policies for Markov Decision Processes

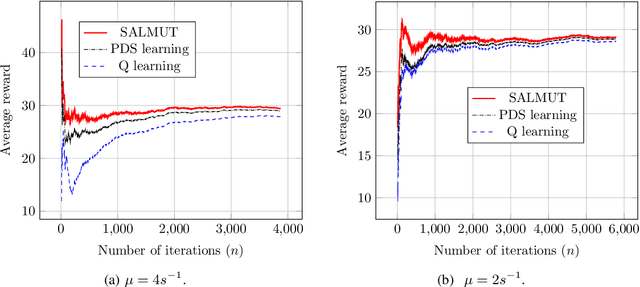
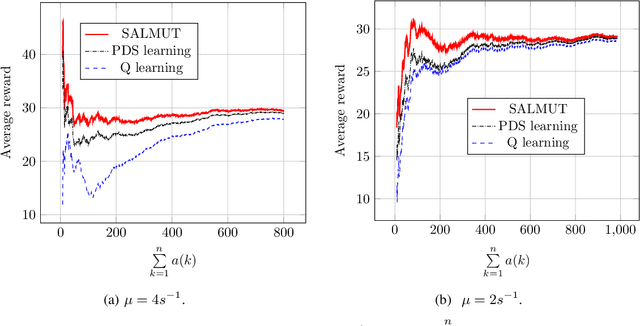
Markov Decision Process (MDP) problems can be solved using Dynamic Programming (DP) methods which suffer from the curse of dimensionality and the curse of modeling. To overcome these issues, Reinforcement Learning (RL) methods are adopted in practice. In this paper, we aim to obtain the optimal admission control policy in a system where different classes of customers are present. Using DP techniques, we prove that it is optimal to admit the $i$ th class of customers only upto a threshold $\tau(i)$ which is a non-increasing function of $i$. Contrary to traditional RL algorithms which do not take into account the structural properties of the optimal policy while learning, we propose a structure-aware learning algorithm which exploits the threshold structure of the optimal policy. We prove the asymptotic convergence of the proposed algorithm to the optimal policy. Due to the reduction in the policy space, the structure-aware learning algorithm provides remarkable improvements in storage and computational complexities over classical RL algorithms. Simulation results also establish the gain in the convergence rate of the proposed algorithm over other RL algorithms. The techniques presented in the paper can be applied to any general MDP problem covering various applications such as inventory management, financial planning and communication networking.

Opinion shaping in social networks using reinforcement learning

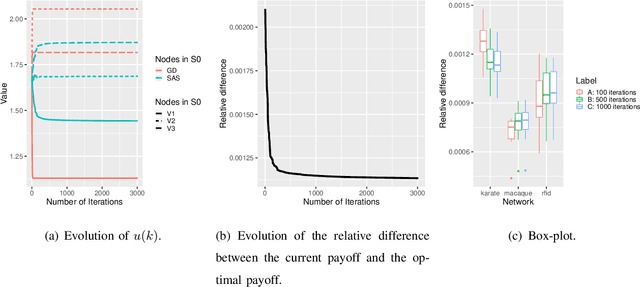
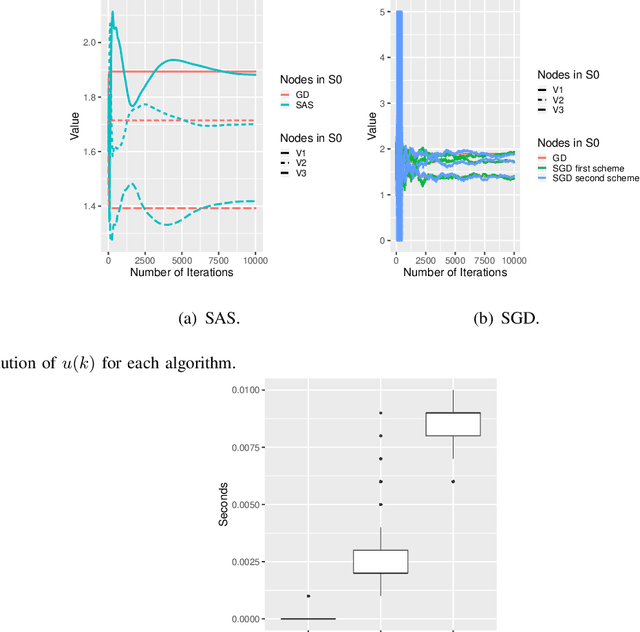
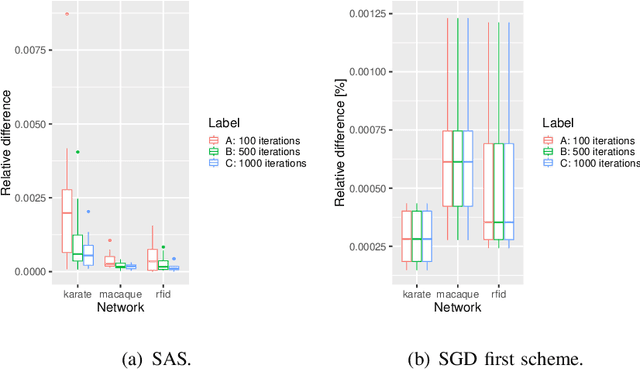
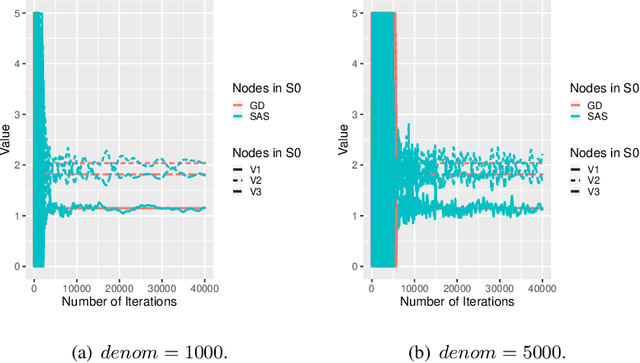
In this paper, we study how to shape opinions in social networks when the matrix of interactions is unknown. We consider classical opinion dynamics with some stubborn agents and the possibility of continuously influencing the opinions of a few selected agents, albeit under resource constraints. We map the opinion dynamics to a value iteration scheme for policy evaluation for a specific stochastic shortest path problem. This leads to a representation of the opinion vector as an approximate value function for a stochastic shortest path problem with some non-classical constraints. We suggest two possible ways of influencing agents. One leads to a convex optimization problem and the other to a non-convex one. Firstly, for both problems, we propose two different online two-time scale reinforcement learning schemes that converge to the optimal solution of each problem. Secondly, we suggest stochastic gradient descent schemes and compare these classes of algorithms with the two-time scale reinforcement learning schemes. Thirdly, we also derive another algorithm designed to tackle the curse of dimensionality one faces when all agents are observed. Numerical studies are provided to illustrate the convergence and efficiency of our algorithms.

A Structure-aware Online Learning Algorithm for Markov Decision Processes

To overcome the curse of dimensionality and curse of modeling in Dynamic Programming (DP) methods for solving classical Markov Decision Process (MDP) problems, Reinforcement Learning (RL) algorithms are popular. In this paper, we consider an infinite-horizon average reward MDP problem and prove the optimality of the threshold policy under certain conditions. Traditional RL techniques do not exploit the threshold nature of optimal policy while learning. In this paper, we propose a new RL algorithm which utilizes the known threshold structure of the optimal policy while learning by reducing the feasible policy space. We establish that the proposed algorithm converges to the optimal policy. It provides a significant improvement in convergence speed and computational and storage complexity over traditional RL algorithms. The proposed technique can be applied to a wide variety of optimization problems that include energy efficient data transmission and management of queues. We exhibit the improvement in convergence speed of the proposed algorithm over other RL algorithms through simulations.

Approachability in Stackelberg Stochastic Games with Vector Costs

The notion of approachability was introduced by Blackwell [1] in the context of vector-valued repeated games. The famous Blackwell's approachability theorem prescribes a strategy for approachability, i.e., for `steering' the average cost of a given agent towards a given target set, irrespective of the strategies of the other agents. In this paper, motivated by the multi-objective optimization/decision making problems in dynamically changing environments, we address the approachability problem in Stackelberg stochastic games with vector valued cost functions. We make two main contributions. Firstly, we give a simple and computationally tractable strategy for approachability for Stackelberg stochastic games along the lines of Blackwell's. Secondly, we give a reinforcement learning algorithm for learning the approachable strategy when the transition kernel is unknown. We also recover as a by-product Blackwell's necessary and sufficient condition for approachability for convex sets in this set up and thus a complete characterization. We also give sufficient conditions for non-convex sets.