The ODE Method for Asymptotic Statistics in Stochastic Approximation and Reinforcement Learning

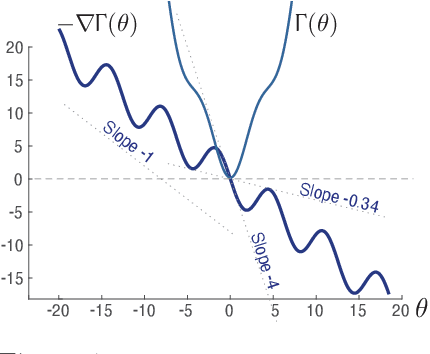
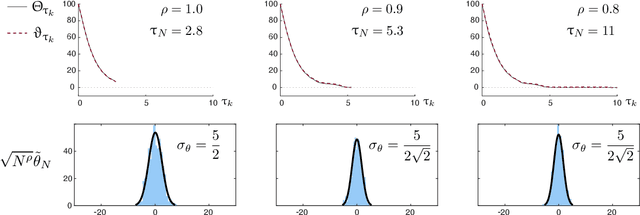
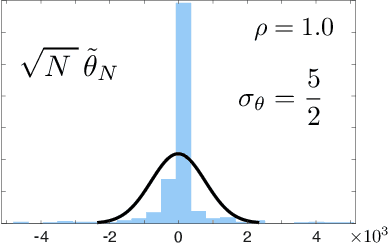
The paper concerns convergence and asymptotic statistics for stochastic approximation driven by Markovian noise: $$ \theta_{n+1}= \theta_n + \alpha_{n + 1} f(\theta_n, \Phi_{n+1}) \,,\quad n\ge 0, $$ in which each $\theta_n\in\Re^d$, $ \{ \Phi_n \}$ is a Markov chain on a general state space X with stationary distribution $\pi$, and $f:\Re^d\times \text{X} \to\Re^d$. In addition to standard Lipschitz bounds on $f$, and conditions on the vanishing step-size sequence $\{\alpha_n\}$, it is assumed that the associated ODE is globally asymptotically stable with stationary point denoted $\theta^*$, where $\bar f(\theta)=E[f(\theta,\Phi)]$ with $\Phi\sim\pi$. Moreover, the ODE@$\infty$ defined with respect to the vector field, $$ \bar f_\infty(\theta):= \lim_{r\to\infty} r^{-1} \bar f(r\theta) \,,\qquad \theta\in\Re^d, $$ is asymptotically stable. The main contributions are summarized as follows: (i) The sequence $\theta$ is convergent if $\Phi$ is geometrically ergodic, and subject to compatible bounds on $f$. The remaining results are established under a stronger assumption on the Markov chain: A slightly weaker version of the Donsker-Varadhan Lyapunov drift condition known as (DV3). (ii) A Lyapunov function is constructed for the joint process $\{\theta_n,\Phi_n\}$ that implies convergence of $\{ \theta_n\}$ in $L_4$. (iii) A functional CLT is established, as well as the usual one-dimensional CLT for the normalized error $z_n:= (\theta_n-\theta^*)/\sqrt{\alpha_n}$. Moment bounds combined with the CLT imply convergence of the normalized covariance, $$ \lim_{n \to \infty} E [ z_n z_n^T ] = \Sigma_\theta, $$ where $\Sigma_\theta$ is the asymptotic covariance appearing in the CLT. (iv) An example is provided where the Markov chain $\Phi$ is geometrically ergodic but it does not satisfy (DV3). While the algorithm is convergent, the second moment is unbounded.

Accelerating Optimization and Reinforcement Learning with Quasi-Stochastic Approximation

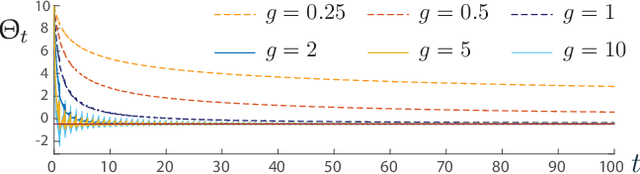
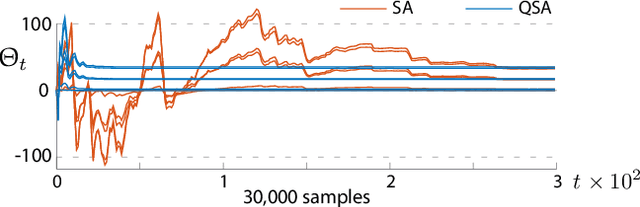
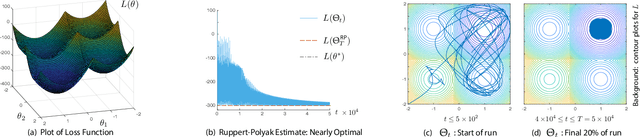
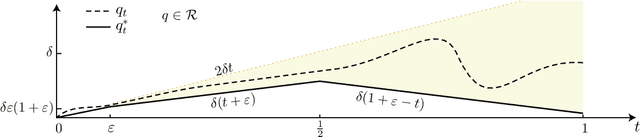
The ODE method has been a workhorse for algorithm design and analysis since the introduction of the stochastic approximation. It is now understood that convergence theory amounts to establishing robustness of Euler approximations for ODEs, while theory of rates of convergence requires finer analysis. This paper sets out to extend this theory to quasi-stochastic approximation, based on algorithms in which the "noise" is based on deterministic signals. The main results are obtained under minimal assumptions: the usual Lipschitz conditions for ODE vector fields, and it is assumed that there is a well defined linearization near the optimal parameter $\theta^*$, with Hurwitz linearization matrix $A^*$. The main contributions are summarized as follows: (i) If the algorithm gain is $a_t=g/(1+t)^\rho$ with $g>0$ and $\rho\in(0,1)$, then the rate of convergence of the algorithm is $1/t^\rho$. There is also a well defined "finite-$t$" approximation: \[ a_t^{-1}\{\Theta_t-\theta^*\}=\bar{Y}+\Xi^{\mathrm{I}}_t+o(1) \] where $\bar{Y}\in\mathbb{R}^d$ is a vector identified in the paper, and $\{\Xi^{\mathrm{I}}_t\}$ is bounded with zero temporal mean. (ii) With gain $a_t = g/(1+t)$ the results are not as sharp: the rate of convergence $1/t$ holds only if $I + g A^*$ is Hurwitz. (iii) Based on the Ruppert-Polyak averaging of stochastic approximation, one would expect that a convergence rate of $1/t$ can be obtained by averaging: \[ \Theta^{\text{RP}}_T=\frac{1}{T}\int_{0}^T \Theta_t\,dt \] where the estimates $\{\Theta_t\}$ are obtained using the gain in (i). The preceding sharp bounds imply that averaging results in $1/t$ convergence rate if and only if $\bar{Y}=\sf 0$. This condition holds if the noise is additive, but appears to fail in general. (iv) The theory is illustrated with applications to gradient-free optimization and policy gradient algorithms for reinforcement learning.