Revisiting Step-Size Assumptions in Stochastic Approximation

Many machine learning and optimization algorithms are built upon the framework of stochastic approximation (SA), for which the selection of step-size (or learning rate) is essential for success. For the sake of clarity, this paper focuses on the special case $\alpha_n = \alpha_0 n^{-\rho}$ at iteration $n$, with $\rho \in [0,1]$ and $\alpha_0>0$ design parameters. It is most common in practice to take $\rho=0$ (constant step-size), while in more theoretically oriented papers a vanishing step-size is preferred. In particular, with $\rho \in (1/2, 1)$ it is known that on applying the averaging technique of Polyak and Ruppert, the mean-squared error (MSE) converges at the optimal rate of $O(1/n)$ and the covariance in the central limit theorem (CLT) is minimal in a precise sense. The paper revisits step-size selection in a general Markovian setting. Under readily verifiable assumptions, the following conclusions are obtained provided $0<\rho<1$: $\bullet$ Parameter estimates converge with probability one, and also in $L_p$ for any $p\ge 1$. $\bullet$ The MSE may converge very slowly for small $\rho$, of order $O(\alpha_n^2)$ even with averaging. $\bullet$ For linear stochastic approximation the source of slow convergence is identified: for any $\rho\in (0,1)$, averaging results in estimates for which the error $\textit{covariance}$ vanishes at the optimal rate, and moreover the CLT covariance is optimal in the sense of Polyak and Ruppert. However, necessary and sufficient conditions are obtained under which the $\textit{bias}$ converges to zero at rate $O(\alpha_n)$. This is the first paper to obtain such strong conclusions while allowing for $\rho \le 1/2$. A major conclusion is that the choice of $\rho =0$ or even $\rho<1/2$ is justified only in select settings -- In general, bias may preclude fast convergence.

The Curse of Memory in Stochastic Approximation: Extended Version

Theory and application of stochastic approximation (SA) has grown within the control systems community since the earliest days of adaptive control. This paper takes a new look at the topic, motivated by recent results establishing remarkable performance of SA with (sufficiently small) constant step-size $\alpha>0$. If averaging is implemented to obtain the final parameter estimate, then the estimates are asymptotically unbiased with nearly optimal asymptotic covariance. These results have been obtained for random linear SA recursions with i.i.d. coefficients. This paper obtains very different conclusions in the more common case of geometrically ergodic Markovian disturbance: (i) The $\textit{target bias}$ is identified, even in the case of non-linear SA, and is in general non-zero. The remaining results are established for linear SA recursions: (ii) the bivariate parameter-disturbance process is geometrically ergodic in a topological sense; (iii) the representation for bias has a simpler form in this case, and cannot be expected to be zero if there is multiplicative noise; (iv) the asymptotic covariance of the averaged parameters is within $O(\alpha)$ of optimal. The error term is identified, and may be massive if mean dynamics are not well conditioned. The theory is illustrated with application to TD-learning.

Convex Q Learning in a Stochastic Environment: Extended Version

The paper introduces the first formulation of convex Q-learning for Markov decision processes with function approximation. The algorithms and theory rest on a relaxation of a dual of Manne's celebrated linear programming characterization of optimal control. The main contributions firstly concern properties of the relaxation, described as a deterministic convex program: we identify conditions for a bounded solution, and a significant relationship between the solution to the new convex program, and the solution to standard Q-learning. The second set of contributions concern algorithm design and analysis: (i) A direct model-free method for approximating the convex program for Q-learning shares properties with its ideal. In particular, a bounded solution is ensured subject to a simple property of the basis functions; (ii) The proposed algorithms are convergent and new techniques are introduced to obtain the rate of convergence in a mean-square sense; (iii) The approach can be generalized to a range of performance criteria, and it is found that variance can be reduced by considering ``relative'' dynamic programming equations; (iv) The theory is illustrated with an application to a classical inventory control problem.

Stability of Q-Learning Through Design and Optimism

Q-learning has become an important part of the reinforcement learning toolkit since its introduction in the dissertation of Chris Watkins in the 1980s. The purpose of this paper is in part a tutorial on stochastic approximation and Q-learning, providing details regarding the INFORMS APS inaugural Applied Probability Trust Plenary Lecture, presented in Nancy France, June 2023. The paper also presents new approaches to ensure stability and potentially accelerated convergence for these algorithms, and stochastic approximation in other settings. Two contributions are entirely new: 1. Stability of Q-learning with linear function approximation has been an open topic for research for over three decades. It is shown that with appropriate optimistic training in the form of a modified Gibbs policy, there exists a solution to the projected Bellman equation, and the algorithm is stable (in terms of bounded parameter estimates). Convergence remains one of many open topics for research. 2. The new Zap Zero algorithm is designed to approximate the Newton-Raphson flow without matrix inversion. It is stable and convergent under mild assumptions on the mean flow vector field for the algorithm, and compatible statistical assumption on an underlying Markov chain. The algorithm is a general approach to stochastic approximation which in particular applies to Q-learning with "oblivious" training even with non-linear function approximation.

Sufficient Exploration for Convex Q-learning

In recent years there has been a collective research effort to find new formulations of reinforcement learning that are simultaneously more efficient and more amenable to analysis. This paper concerns one approach that builds on the linear programming (LP) formulation of optimal control of Manne. A primal version is called logistic Q-learning, and a dual variant is convex Q-learning. This paper focuses on the latter, while building bridges with the former. The main contributions follow: (i) The dual of convex Q-learning is not precisely Manne's LP or a version of logistic Q-learning, but has similar structure that reveals the need for regularization to avoid over-fitting. (ii) A sufficient condition is obtained for a bounded solution to the Q-learning LP. (iii) Simulation studies reveal numerical challenges when addressing sampled-data systems based on a continuous time model. The challenge is addressed using state-dependent sampling. The theory is illustrated with applications to examples from OpenAI gym. It is shown that convex Q-learning is successful in cases where standard Q-learning diverges, such as the LQR problem.

Model-Free Characterizations of the Hamilton-Jacobi-Bellman Equation and Convex Q-Learning in Continuous Time

Convex Q-learning is a recent approach to reinforcement learning, motivated by the possibility of a firmer theory for convergence, and the possibility of making use of greater a priori knowledge regarding policy or value function structure. This paper explores algorithm design in the continuous time domain, with finite-horizon optimal control objective. The main contributions are (i) Algorithm design is based on a new Q-ODE, which defines the model-free characterization of the Hamilton-Jacobi-Bellman equation. (ii) The Q-ODE motivates a new formulation of Convex Q-learning that avoids the approximations appearing in prior work. The Bellman error used in the algorithm is defined by filtered measurements, which is beneficial in the presence of measurement noise. (iii) A characterization of boundedness of the constraint region is obtained through a non-trivial extension of recent results from the discrete time setting. (iv) The theory is illustrated in application to resource allocation for distributed energy resources, for which the theory is ideally suited.

The ODE Method for Asymptotic Statistics in Stochastic Approximation and Reinforcement Learning

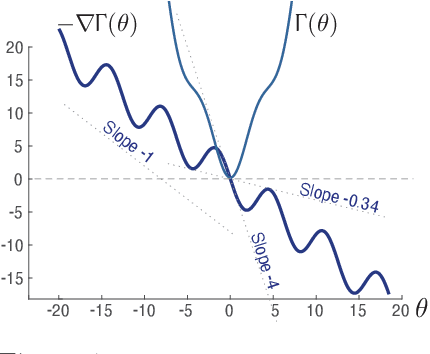
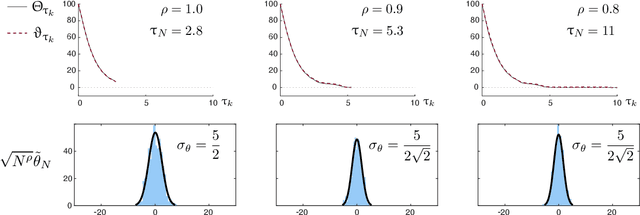
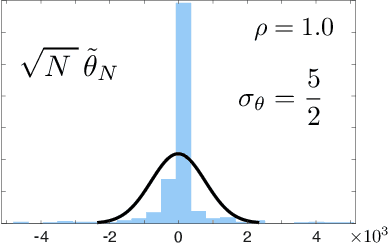
The paper concerns convergence and asymptotic statistics for stochastic approximation driven by Markovian noise: $$ \theta_{n+1}= \theta_n + \alpha_{n + 1} f(\theta_n, \Phi_{n+1}) \,,\quad n\ge 0, $$ in which each $\theta_n\in\Re^d$, $ \{ \Phi_n \}$ is a Markov chain on a general state space X with stationary distribution $\pi$, and $f:\Re^d\times \text{X} \to\Re^d$. In addition to standard Lipschitz bounds on $f$, and conditions on the vanishing step-size sequence $\{\alpha_n\}$, it is assumed that the associated ODE is globally asymptotically stable with stationary point denoted $\theta^*$, where $\bar f(\theta)=E[f(\theta,\Phi)]$ with $\Phi\sim\pi$. Moreover, the ODE@$\infty$ defined with respect to the vector field, $$ \bar f_\infty(\theta):= \lim_{r\to\infty} r^{-1} \bar f(r\theta) \,,\qquad \theta\in\Re^d, $$ is asymptotically stable. The main contributions are summarized as follows: (i) The sequence $\theta$ is convergent if $\Phi$ is geometrically ergodic, and subject to compatible bounds on $f$. The remaining results are established under a stronger assumption on the Markov chain: A slightly weaker version of the Donsker-Varadhan Lyapunov drift condition known as (DV3). (ii) A Lyapunov function is constructed for the joint process $\{\theta_n,\Phi_n\}$ that implies convergence of $\{ \theta_n\}$ in $L_4$. (iii) A functional CLT is established, as well as the usual one-dimensional CLT for the normalized error $z_n:= (\theta_n-\theta^*)/\sqrt{\alpha_n}$. Moment bounds combined with the CLT imply convergence of the normalized covariance, $$ \lim_{n \to \infty} E [ z_n z_n^T ] = \Sigma_\theta, $$ where $\Sigma_\theta$ is the asymptotic covariance appearing in the CLT. (iv) An example is provided where the Markov chain $\Phi$ is geometrically ergodic but it does not satisfy (DV3). While the algorithm is convergent, the second moment is unbounded.

Accelerating Optimization and Reinforcement Learning with Quasi-Stochastic Approximation

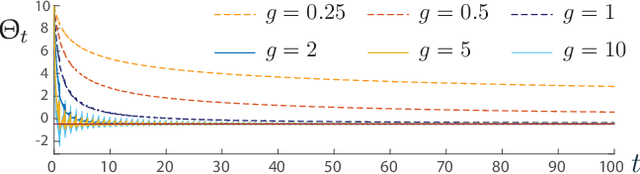
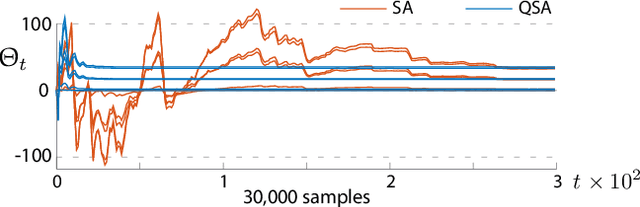
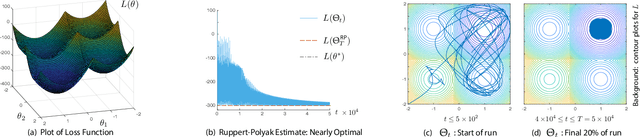
The ODE method has been a workhorse for algorithm design and analysis since the introduction of the stochastic approximation. It is now understood that convergence theory amounts to establishing robustness of Euler approximations for ODEs, while theory of rates of convergence requires finer analysis. This paper sets out to extend this theory to quasi-stochastic approximation, based on algorithms in which the "noise" is based on deterministic signals. The main results are obtained under minimal assumptions: the usual Lipschitz conditions for ODE vector fields, and it is assumed that there is a well defined linearization near the optimal parameter $\theta^*$, with Hurwitz linearization matrix $A^*$. The main contributions are summarized as follows: (i) If the algorithm gain is $a_t=g/(1+t)^\rho$ with $g>0$ and $\rho\in(0,1)$, then the rate of convergence of the algorithm is $1/t^\rho$. There is also a well defined "finite-$t$" approximation: \[ a_t^{-1}\{\Theta_t-\theta^*\}=\bar{Y}+\Xi^{\mathrm{I}}_t+o(1) \] where $\bar{Y}\in\mathbb{R}^d$ is a vector identified in the paper, and $\{\Xi^{\mathrm{I}}_t\}$ is bounded with zero temporal mean. (ii) With gain $a_t = g/(1+t)$ the results are not as sharp: the rate of convergence $1/t$ holds only if $I + g A^*$ is Hurwitz. (iii) Based on the Ruppert-Polyak averaging of stochastic approximation, one would expect that a convergence rate of $1/t$ can be obtained by averaging: \[ \Theta^{\text{RP}}_T=\frac{1}{T}\int_{0}^T \Theta_t\,dt \] where the estimates $\{\Theta_t\}$ are obtained using the gain in (i). The preceding sharp bounds imply that averaging results in $1/t$ convergence rate if and only if $\bar{Y}=\sf 0$. This condition holds if the noise is additive, but appears to fail in general. (iv) The theory is illustrated with applications to gradient-free optimization and policy gradient algorithms for reinforcement learning.

Explicit Mean-Square Error Bounds for Monte-Carlo and Linear Stochastic Approximation

This paper concerns error bounds for recursive equations subject to Markovian disturbances. Motivating examples abound within the fields of Markov chain Monte Carlo (MCMC) and Reinforcement Learning (RL), and many of these algorithms can be interpreted as special cases of stochastic approximation (SA). It is argued that it is not possible in general to obtain a Hoeffding bound on the error sequence, even when the underlying Markov chain is reversible and geometrically ergodic, such as the M/M/1 queue. This is motivation for the focus on mean square error bounds for parameter estimates. It is shown that mean square error achieves the optimal rate of $O(1/n)$, subject to conditions on the step-size sequence. Moreover, the exact constants in the rate are obtained, which is of great value in algorithm design.

Zap Q-Learning With Nonlinear Function Approximation

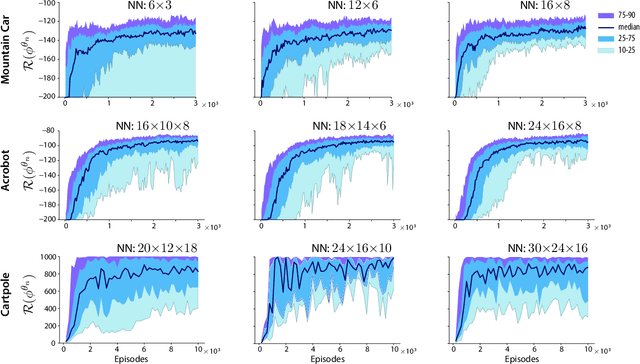
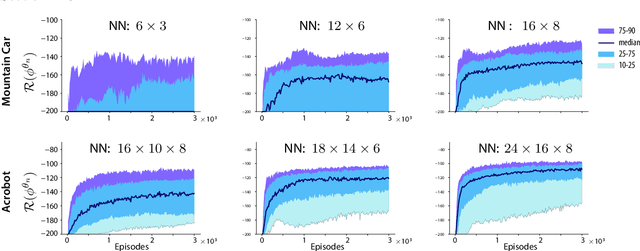
The Zap stochastic approximation (SA) algorithm was introduced recently as a means to accelerate convergence in reinforcement learning algorithms. While numerical results were impressive, stability (in the sense of boundedness of parameter estimates) was established in only a few special cases. This class of algorithms is generalized in this paper, and stability is established under very general conditions. This general result can be applied to a wide range of algorithms found in reinforcement learning. Two classes are considered in this paper: (i)The natural generalization of Watkins' algorithm is not always stable in function approximation settings. Parameter estimates may diverge to infinity even in the \textit{linear} function approximation setting with a simple finite state-action MDP. Under mild conditions, the Zap SA algorithm provides a stable algorithm, even in the case of \textit{nonlinear} function approximation. (ii) The GQ algorithm of Maei et.~al.~2010 is designed to address the stability challenge. Analysis is provided to explain why the algorithm may be very slow to converge in practice. The new Zap GQ algorithm is stable even for nonlinear function approximation.