Gaussian Imagination in Bandit Learning

Assuming distributions are Gaussian often facilitates computations that are otherwise intractable. We study the performance of an agent that attains a bounded information ratio with respect to a bandit environment with a Gaussian prior distribution and a Gaussian likelihood function when applied instead to a Bernoulli bandit. Relative to an information-theoretic bound on the Bayesian regret the agent would incur when interacting with the Gaussian bandit, we bound the increase in regret when the agent interacts with the Bernoulli bandit. If the Gaussian prior distribution and likelihood function are sufficiently diffuse, this increase grows at a rate which is at most linear in the square-root of the time horizon, and thus the per-timestep increase vanishes. Our results formalize the folklore that so-called Bayesian agents remain effective when instantiated with diffuse misspecified distributions.

A Bit Better? Quantifying Information for Bandit Learning

The information ratio offers an approach to assessing the efficacy with which an agent balances between exploration and exploitation. Originally, this was defined to be the ratio between squared expected regret and the mutual information between the environment and action-observation pair, which represents a measure of information gain. Recent work has inspired consideration of alternative information measures, particularly for use in analysis of bandit learning algorithms to arrive at tighter regret bounds. We investigate whether quantification of information via such alternatives can improve the realized performance of information-directed sampling, which aims to minimize the information ratio.

Q-learning with Uniformly Bounded Variance: Large Discounting is Not a Barrier to Fast Learning

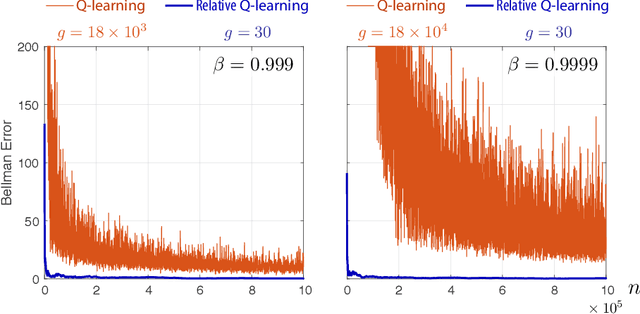
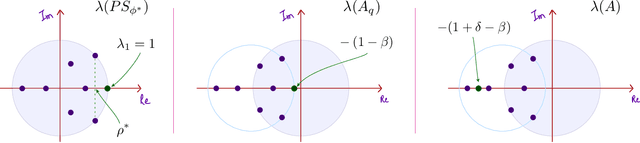
It has been a trend in the Reinforcement Learning literature to derive sample complexity bounds: a bound on how many experiences with the environment are required to obtain an $\varepsilon$-optimal policy. In the discounted cost, infinite horizon setting, all of the known bounds have a factor that is a polynomial in $1/(1-\beta)$, where $\beta < 1$ is the discount factor. For a large discount factor, these bounds seem to imply that a very large number of samples is required to achieve an $\varepsilon$-optimal policy. The objective of the present work is to introduce a new class of algorithms that have sample complexity uniformly bounded for all $\beta < 1$. One may argue that this is impossible, due to a recent min-max lower bound. The explanation is that this previous lower bound is for a specific problem, which we modify, without compromising the ultimate objective of obtaining an $\varepsilon$-optimal policy. Specifically, we show that the asymptotic variance of the Q-learning algorithm, with an optimized step-size sequence, is a quadratic function of $1/(1-\beta)$; an expected, and essentially known result. The new relative Q-learning algorithm proposed here is shown to have asymptotic variance that is a quadratic in $1/(1- \rho \beta)$, where $1 - \rho > 0$ is the spectral gap of an optimal transition matrix.

Explicit Mean-Square Error Bounds for Monte-Carlo and Linear Stochastic Approximation

This paper concerns error bounds for recursive equations subject to Markovian disturbances. Motivating examples abound within the fields of Markov chain Monte Carlo (MCMC) and Reinforcement Learning (RL), and many of these algorithms can be interpreted as special cases of stochastic approximation (SA). It is argued that it is not possible in general to obtain a Hoeffding bound on the error sequence, even when the underlying Markov chain is reversible and geometrically ergodic, such as the M/M/1 queue. This is motivation for the focus on mean square error bounds for parameter estimates. It is shown that mean square error achieves the optimal rate of $O(1/n)$, subject to conditions on the step-size sequence. Moreover, the exact constants in the rate are obtained, which is of great value in algorithm design.

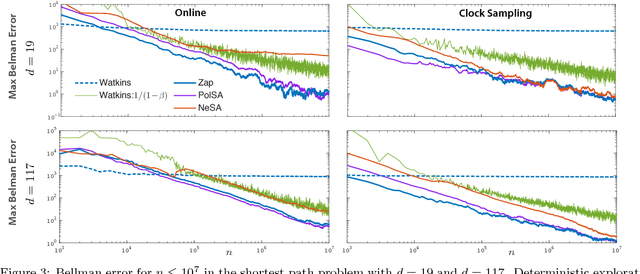
Zap Q-Learning With Nonlinear Function Approximation

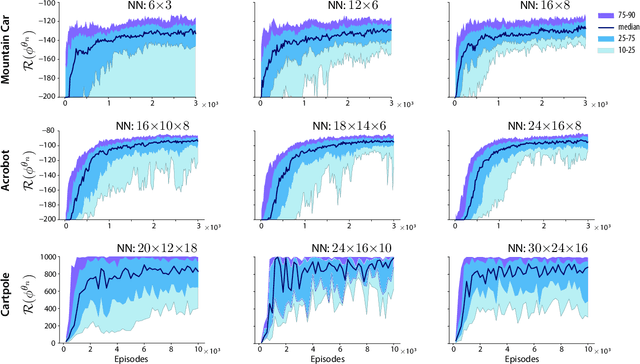
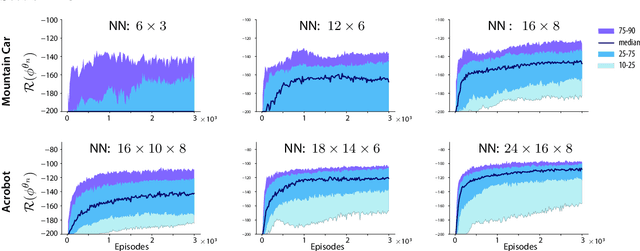
The Zap stochastic approximation (SA) algorithm was introduced recently as a means to accelerate convergence in reinforcement learning algorithms. While numerical results were impressive, stability (in the sense of boundedness of parameter estimates) was established in only a few special cases. This class of algorithms is generalized in this paper, and stability is established under very general conditions. This general result can be applied to a wide range of algorithms found in reinforcement learning. Two classes are considered in this paper: (i)The natural generalization of Watkins' algorithm is not always stable in function approximation settings. Parameter estimates may diverge to infinity even in the \textit{linear} function approximation setting with a simple finite state-action MDP. Under mild conditions, the Zap SA algorithm provides a stable algorithm, even in the case of \textit{nonlinear} function approximation. (ii) The GQ algorithm of Maei et.~al.~2010 is designed to address the stability challenge. Analysis is provided to explain why the algorithm may be very slow to converge in practice. The new Zap GQ algorithm is stable even for nonlinear function approximation.

Stochastic Variance Reduced Primal Dual Algorithms for Empirical Composition Optimization

We consider a generic empirical composition optimization problem, where there are empirical averages present both outside and inside nonlinear loss functions. Such a problem is of interest in various machine learning applications, and cannot be directly solved by standard methods such as stochastic gradient descent (SGD). We take a novel approach to solving this problem by reformulating the original minimization objective into an equivalent min-max objective, which brings out all the empirical averages that are originally inside the nonlinear loss functions. We exploit the rich structures of the reformulated problem and develop a stochastic primal-dual algorithm, SVRPDA-I, to solve the problem efficiently. We carry out extensive theoretical analysis of the proposed algorithm, obtaining the convergence rate, the total computation complexity and the storage complexity. In particular, the algorithm is shown to converge at a linear rate when the problem is strongly convex. Moreover, we also develop an approximate version of the algorithm, SVRPDA-II, which further reduces the memory requirement. Finally, we evaluate the performance of our algorithms on several real-world benchmarks, and experimental results show that the proposed algorithms significantly outperform existing techniques.

Zap Q-Learning for Optimal Stopping Time Problems

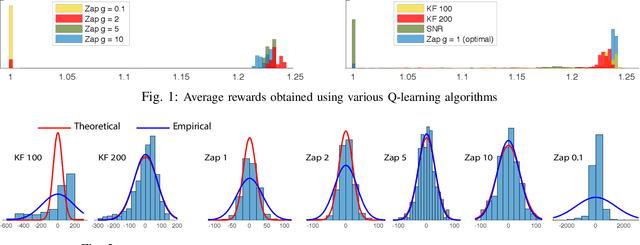
We propose a novel reinforcement learning algorithm that approximates solutions to the problem of discounted optimal stopping in an irreducible, uniformly ergodic Markov chain evolving on a compact subset of $\mathbb R^n$. A dynamic programming approach has been taken by Tsitsikilis and Van Roy to solve this problem, wherein they propose a Q-learning algorithm to estimate the value function, in a linear function approximation setting. The Zap-Q learning algorithm proposed in this work is the first algorithm that is designed to achieve optimal asymptotic variance. We prove convergence of the algorithm using ODE analysis, and the optimal asymptotic variance property is reflected via fast convergence in a finance example.

Differential Temporal Difference Learning

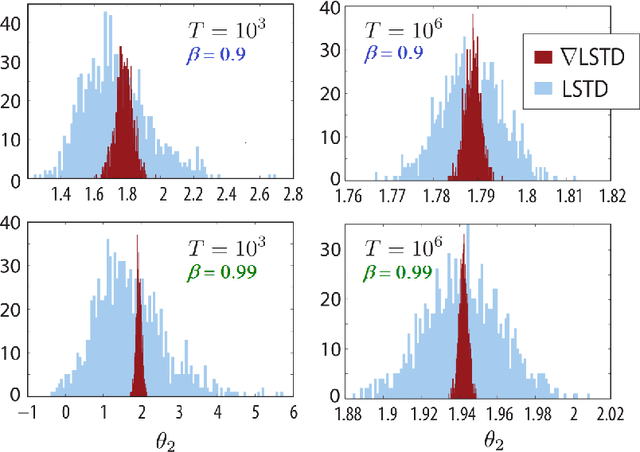
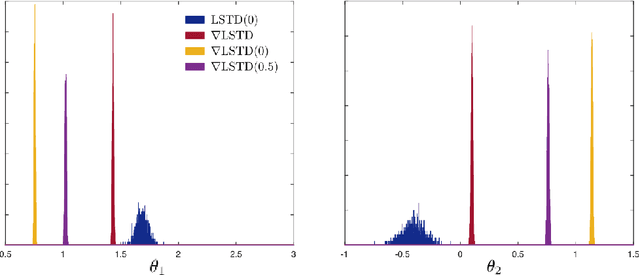
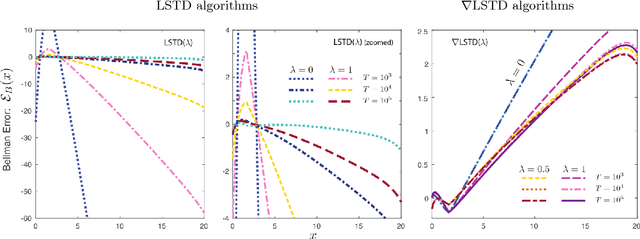
Value functions derived from Markov decision processes arise as a central component of algorithms as well as performance metrics in many statistics and engineering applications of machine learning techniques. Computation of the solution to the associated Bellman equations is challenging in most practical cases of interest. A popular class of approximation techniques, known as Temporal Difference (TD) learning algorithms, are an important sub-class of general reinforcement learning methods. The algorithms introduced in this paper are intended to resolve two well-known difficulties of TD-learning approaches: Their slow convergence due to very high variance, and the fact that, for the problem of computing the relative value function, consistent algorithms exist only in special cases. First we show that the gradients of these value functions admit a representation that lends itself to algorithm design. Based on this result, a new class of differential TD-learning algorithms is introduced. For Markovian models on Euclidean space with smooth dynamics, the algorithms are shown to be consistent under general conditions. Numerical results show dramatic variance reduction when compared to standard methods.

Zap Meets Momentum: Stochastic Approximation Algorithms with Optimal Convergence Rate

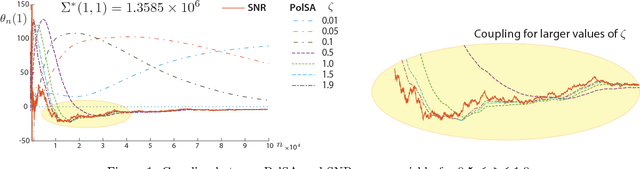
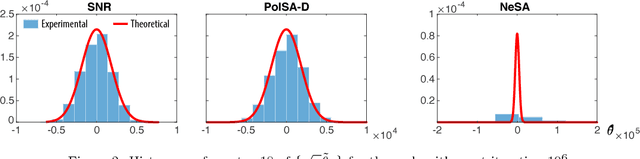
There are two well known Stochastic Approximation techniques that are known to have optimal rate of convergence (measured in terms of asymptotic variance): the Ruppert-Polyak averaging technique, and stochastic Newton-Raphson (SNR) (a matrix gain algorithm that resembles the deterministic Newton-Raphson method). The Zap algorithms introduced by the authors are a version of SNR designed to behave more closely like their deterministic cousin. It is found that estimates from the Zap Q-learning algorithm converge remarkably quickly, but the per-iteration complexity can be high. This paper introduces an entirely new class of stochastic approximation algorithms based on matrix momentum. For a special choice of the matrix momentum and gain sequences, it is found in simulations that the parameter estimates obtained from the algorithm couple with those obtained from the more complex stochastic Newton-Raphson algorithm. Conditions under which coupling is guaranteed are established for a class of linear recursions. Optimal finite-$n$ error bounds are also obtained. The main objective of this work is to create more efficient algorithms for applications to reinforcement learning. Numerical results illustrate the value of these techniques in this setting.

Fastest Convergence for Q-learning

The Zap Q-learning algorithm introduced in this paper is an improvement of Watkins' original algorithm and recent competitors in several respects. It is a matrix-gain algorithm designed so that its asymptotic variance is optimal. Moreover, an ODE analysis suggests that the transient behavior is a close match to a deterministic Newton-Raphson implementation. This is made possible by a two time-scale update equation for the matrix gain sequence. The analysis suggests that the approach will lead to stable and efficient computation even for non-ideal parameterized settings. Numerical experiments confirm the quick convergence, even in such non-ideal cases. A secondary goal of this paper is tutorial. The first half of the paper contains a survey on reinforcement learning algorithms, with a focus on minimum variance algorithms.