SKETCH: Semantic Key-Point Conditioning for Long-Horizon Vessel Trajectory Prediction

Accurate long-horizon vessel trajectory prediction remains challenging due to compounded uncertainty from complex navigation behaviors and environmental factors. Existing methods often struggle to maintain global directional consistency, leading to drifting or implausible trajectories when extrapolated over long time horizons. To address this issue, we propose a semantic-key-point-conditioned trajectory modeling framework, in which future trajectories are predicted by conditioning on a high-level Next Key Point (NKP) that captures navigational intent. This formulation decomposes long-horizon prediction into global semantic decision-making and local motion modeling, effectively restricting the support of future trajectories to semantically feasible subsets. To efficiently estimate the NKP prior from historical observations, we adopt a pretrain-finetune strategy. Extensive experiments on real-world AIS data demonstrate that the proposed method consistently outperforms state-of-the-art approaches, particularly for long travel durations, directional accuracy, and fine-grained trajectory prediction.

NeRF-MIR: Towards High-Quality Restoration of Masked Images with Neural Radiance Fields

Neural Radiance Fields (NeRF) have demonstrated remarkable performance in novel view synthesis. However, there is much improvement room on restoring 3D scenes based on NeRF from corrupted images, which are common in natural scene captures and can significantly impact the effectiveness of NeRF. This paper introduces NeRF-MIR, a novel neural rendering approach specifically proposed for the restoration of masked images, demonstrating the potential of NeRF in this domain. Recognizing that randomly emitting rays to pixels in NeRF may not effectively learn intricate image textures, we propose a \textbf{P}atch-based \textbf{E}ntropy for \textbf{R}ay \textbf{E}mitting (\textbf{PERE}) strategy to distribute emitted rays properly. This enables NeRF-MIR to fuse comprehensive information from images of different views. Additionally, we introduce a \textbf{P}rogressively \textbf{I}terative \textbf{RE}storation (\textbf{PIRE}) mechanism to restore the masked regions in a self-training process. Furthermore, we design a dynamically-weighted loss function that automatically recalibrates the loss weights for masked regions. As existing datasets do not support NeRF-based masked image restoration, we construct three masked datasets to simulate corrupted scenarios. Extensive experiments on real data and constructed datasets demonstrate the superiority of NeRF-MIR over its counterparts in masked image restoration.

IDDR-NGP: Incorporating Detectors for Distractor Removal with Instant Neural Radiance Field

This paper presents the first unified distractor removal method, named IDDR-NGP, which directly operates on Instant-NPG. The method is able to remove a wide range of distractors in 3D scenes, such as snowflakes, confetti, defoliation and petals, whereas existing methods usually focus on a specific type of distractors. By incorporating implicit 3D representations with 2D detectors, we demonstrate that it is possible to efficiently restore 3D scenes from multiple corrupted images. We design the learned perceptual image patch similarity~( LPIPS) loss and the multi-view compensation loss (MVCL) to jointly optimize the rendering results of IDDR-NGP, which could aggregate information from multi-view corrupted images. All of them can be trained in an end-to-end manner to synthesize high-quality 3D scenes. To support the research on distractors removal in implicit 3D representations, we build a new benchmark dataset that consists of both synthetic and real-world distractors. To validate the effectiveness and robustness of IDDR-NGP, we provide a wide range of distractors with corresponding annotated labels added to both realistic and synthetic scenes. Extensive experimental results demonstrate the effectiveness and robustness of IDDR-NGP in removing multiple types of distractors. In addition, our approach achieves results comparable with the existing SOTA desnow methods and is capable of accurately removing both realistic and synthetic distractors.

CogFlow: Bridging Perception and Reasoning through Knowledge Internalization for Visual Mathematical Problem Solving

Despite significant progress, multimodal large language models continue to struggle with visual mathematical problem solving. Some recent works recognize that visual perception is a bottleneck in visual mathematical reasoning, but their solutions are limited to improving the extraction and interpretation of visual inputs. Notably, they all ignore the key issue of whether the extracted visual cues are faithfully integrated and properly utilized in subsequent reasoning. Motivated by this, we present CogFlow, a novel cognitive-inspired three-stage framework that incorporates a knowledge internalization stage, explicitly simulating the hierarchical flow of human reasoning: perception$\Rightarrow$internalization$\Rightarrow$reasoning. Inline with this hierarchical flow, we holistically enhance all its stages. We devise Synergistic Visual Rewards to boost perception capabilities in parametric and semantic spaces, jointly improving visual information extraction from symbols and diagrams. To guarantee faithful integration of extracted visual cues into subsequent reasoning, we introduce a Knowledge Internalization Reward model in the internalization stage, bridging perception and reasoning. Moreover, we design a Visual-Gated Policy Optimization algorithm to further enforce the reasoning is grounded with the visual knowledge, preventing models seeking shortcuts that appear coherent but are visually ungrounded reasoning chains. Moreover, we contribute a new dataset MathCog for model training, which contains samples with over 120K high-quality perception-reasoning aligned annotations. Comprehensive experiments and analysis on commonly used visual mathematical reasoning benchmarks validate the superiority of the proposed CogFlow.

Align$^3$GR: Unified Multi-Level Alignment for LLM-based Generative Recommendation

Large Language Models (LLMs) demonstrate significant advantages in leveraging structured world knowledge and multi-step reasoning capabilities. However, fundamental challenges arise when transforming LLMs into real-world recommender systems due to semantic and behavioral misalignment. To bridge this gap, we propose Align$^3$GR, a novel framework that unifies token-level, behavior modeling-level, and preference-level alignment. Our approach introduces: Dual tokenization fusing user-item semantic and collaborative signals. Enhanced behavior modeling with bidirectional semantic alignment. Progressive DPO strategy combining self-play (SP-DPO) and real-world feedback (RF-DPO) for dynamic preference adaptation. Experiments show Align$^3$GR outperforms the SOTA baseline by +17.8% in Recall@10 and +20.2% in NDCG@10 on the public dataset, with significant gains in online A/B tests and full-scale deployment on an industrial large-scale recommendation platform.

SAMora: Enhancing SAM through Hierarchical Self-Supervised Pre-Training for Medical Images

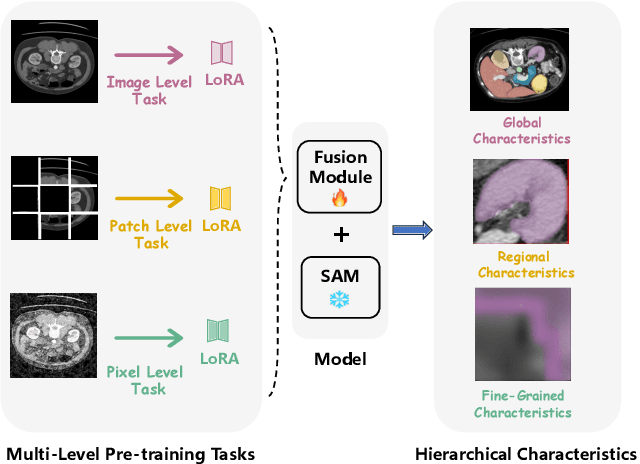
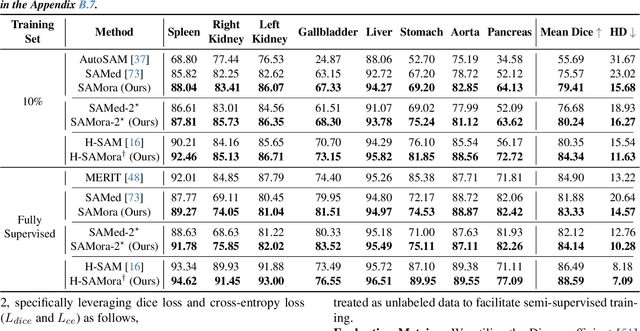
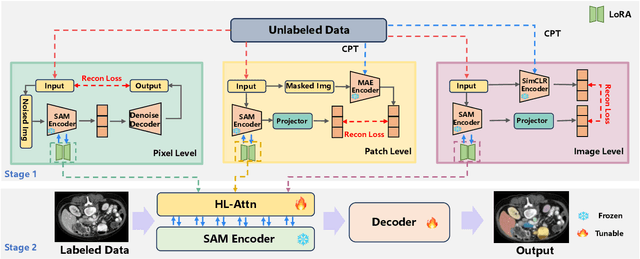
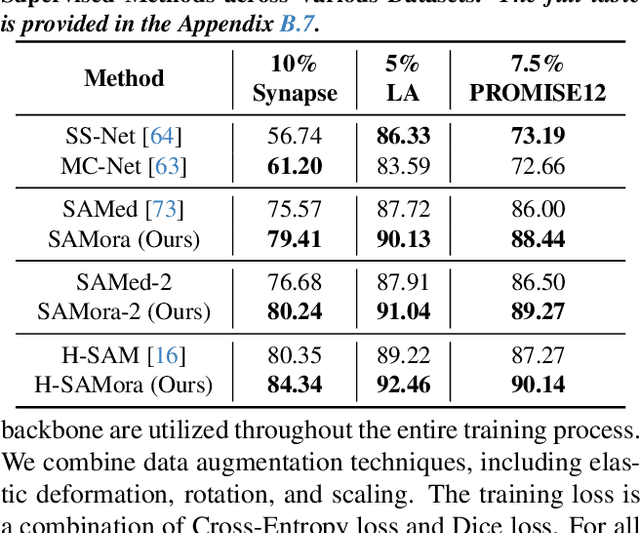
The Segment Anything Model (SAM) has demonstrated significant potential in medical image segmentation. Yet, its performance is limited when only a small amount of labeled data is available, while there is abundant valuable yet often overlooked hierarchical information in medical data. To address this limitation, we draw inspiration from self-supervised learning and propose SAMora, an innovative framework that captures hierarchical medical knowledge by applying complementary self-supervised learning objectives at the image, patch, and pixel levels. To fully exploit the complementarity of hierarchical knowledge within LoRAs, we introduce HL-Attn, a hierarchical fusion module that integrates multi-scale features while maintaining their distinct characteristics. SAMora is compatible with various SAM variants, including SAM2, SAMed, and H-SAM. Experimental results on the Synapse, LA, and PROMISE12 datasets demonstrate that SAMora outperforms existing SAM variants. It achieves state-of-the-art performance in both few-shot and fully supervised settings while reducing fine-tuning epochs by 90%. The code is available at https://github.com/ShChen233/SAMora.

The ODE Method for Stochastic Approximation and Reinforcement Learning with Markovian Noise

Stochastic approximation is a class of algorithms that update a vector iteratively, incrementally, and stochastically, including, e.g., stochastic gradient descent and temporal difference learning. One fundamental challenge in analyzing a stochastic approximation algorithm is to establish its stability, i.e., to show that the stochastic vector iterates are bounded almost surely. In this paper, we extend the celebrated Borkar-Meyn theorem for stability from the Martingale difference noise setting to the Markovian noise setting, which greatly improves its applicability in reinforcement learning, especially in those off-policy reinforcement learning algorithms with linear function approximation and eligibility traces. Central to our analysis is the diminishing asymptotic rate of change of a few functions, which is implied by both a form of strong law of large numbers and a commonly used V4 Lyapunov drift condition and trivially holds if the Markov chain is finite and irreducible.

GRID: A Platform for General Robot Intelligence Development

Developing machine intelligence abilities in robots and autonomous systems is an expensive and time consuming process. Existing solutions are tailored to specific applications and are harder to generalize. Furthermore, scarcity of training data adds a layer of complexity in deploying deep machine learning models. We present a new platform for General Robot Intelligence Development (GRID) to address both of these issues. The platform enables robots to learn, compose and adapt skills to their physical capabilities, environmental constraints and goals. The platform addresses AI problems in robotics via foundation models that know the physical world. GRID is designed from the ground up to be extensible to accommodate new types of robots, vehicles, hardware platforms and software protocols. In addition, the modular design enables various deep ML components and existing foundation models to be easily usable in a wider variety of robot-centric problems. We demonstrate the platform in various aerial robotics scenarios and demonstrate how the platform dramatically accelerates development of machine intelligent robots.

Is Imitation All You Need? Generalized Decision-Making with Dual-Phase Training

We introduce DualMind, a generalist agent designed to tackle various decision-making tasks that addresses challenges posed by current methods, such as overfitting behaviors and dependence on task-specific fine-tuning. DualMind uses a novel "Dual-phase" training strategy that emulates how humans learn to act in the world. The model first learns fundamental common knowledge through a self-supervised objective tailored for control tasks and then learns how to make decisions based on different contexts through imitating behaviors conditioned on given prompts. DualMind can handle tasks across domains, scenes, and embodiments using just a single set of model weights and can execute zero-shot prompting without requiring task-specific fine-tuning. We evaluate DualMind on MetaWorld and Habitat through extensive experiments and demonstrate its superior generalizability compared to previous techniques, outperforming other generalist agents by over 50$\%$ and 70$\%$ on Habitat and MetaWorld, respectively. On the 45 tasks in MetaWorld, DualMind achieves over 30 tasks at a 90$\%$ success rate.

PACT: Perception-Action Causal Transformer for Autoregressive Robotics Pre-Training

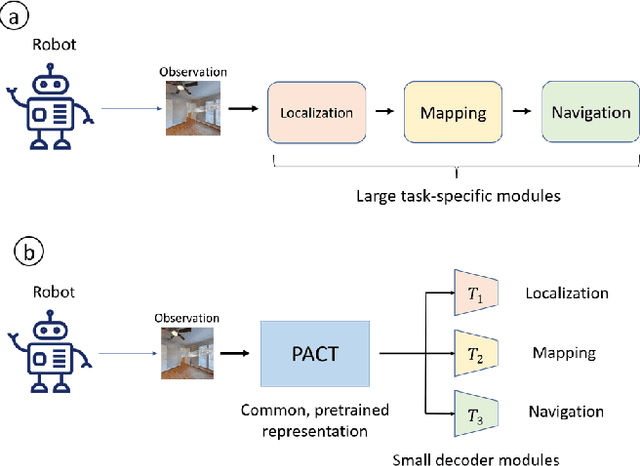
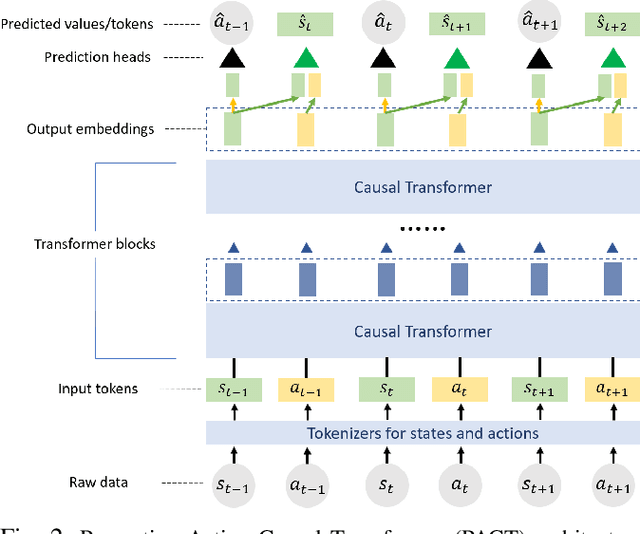
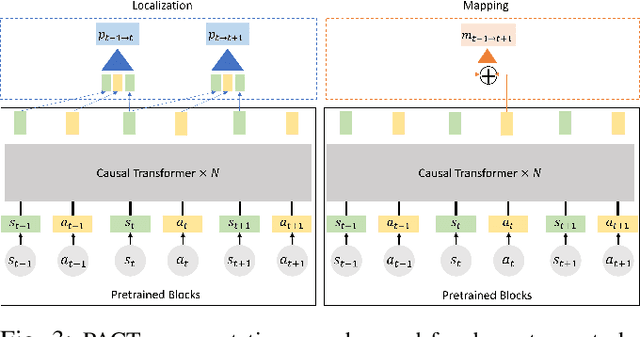
Robotics has long been a field riddled with complex systems architectures whose modules and connections, whether traditional or learning-based, require significant human expertise and prior knowledge. Inspired by large pre-trained language models, this work introduces a paradigm for pre-training a general purpose representation that can serve as a starting point for multiple tasks on a given robot. We present the Perception-Action Causal Transformer (PACT), a generative transformer-based architecture that aims to build representations directly from robot data in a self-supervised fashion. Through autoregressive prediction of states and actions over time, our model implicitly encodes dynamics and behaviors for a particular robot. Our experimental evaluation focuses on the domain of mobile agents, where we show that this robot-specific representation can function as a single starting point to achieve distinct tasks such as safe navigation, localization and mapping. We evaluate two form factors: a wheeled robot that uses a LiDAR sensor as perception input (MuSHR), and a simulated agent that uses first-person RGB images (Habitat). We show that finetuning small task-specific networks on top of the larger pretrained model results in significantly better performance compared to training a single model from scratch for all tasks simultaneously, and comparable performance to training a separate large model for each task independently. By sharing a common good-quality representation across tasks we can lower overall model capacity and speed up the real-time deployment of such systems.