Experience Replay Addresses Loss of Plasticity in Continual Learning

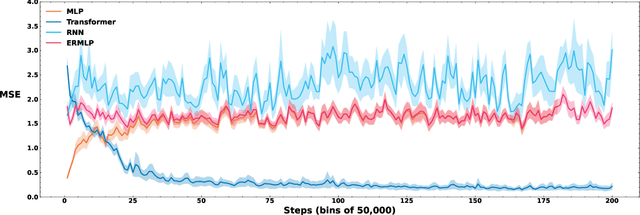
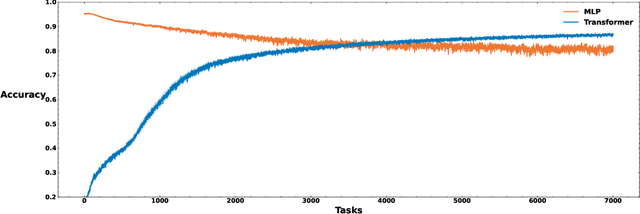
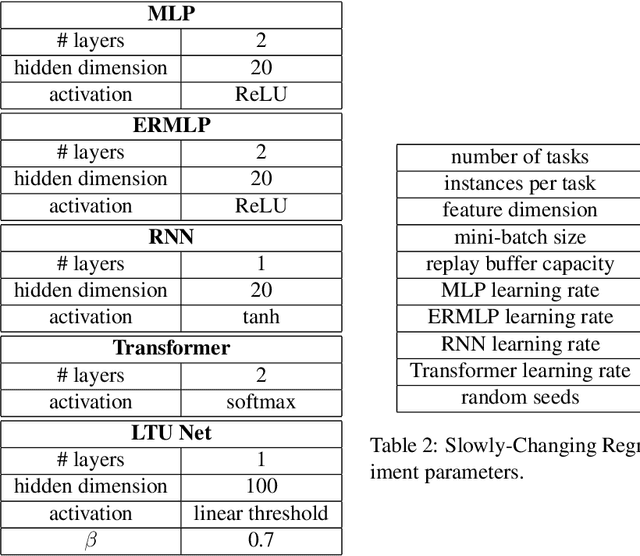
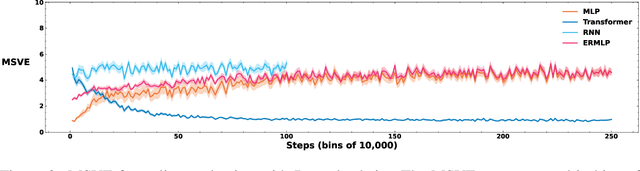
Loss of plasticity is one of the main challenges in continual learning with deep neural networks, where neural networks trained via backpropagation gradually lose their ability to adapt to new tasks and perform significantly worse than their freshly initialized counterparts. The main contribution of this paper is to propose a new hypothesis that experience replay addresses the loss of plasticity in continual learning. Here, experience replay is a form of memory. We provide supporting evidence for this hypothesis. In particular, we demonstrate in multiple different tasks, including regression, classification, and policy evaluation, that by simply adding an experience replay and processing the data in the experience replay with Transformers, the loss of plasticity disappears. Notably, we do not alter any standard components of deep learning. For example, we do not change backpropagation. We do not modify the activation functions. And we do not use any regularization. We conjecture that experience replay and Transformers can address the loss of plasticity because of the in-context learning phenomenon.

GameChat: Multi-LLM Dialogue for Safe, Agile, and Socially Optimal Multi-Agent Navigation in Constrained Environments

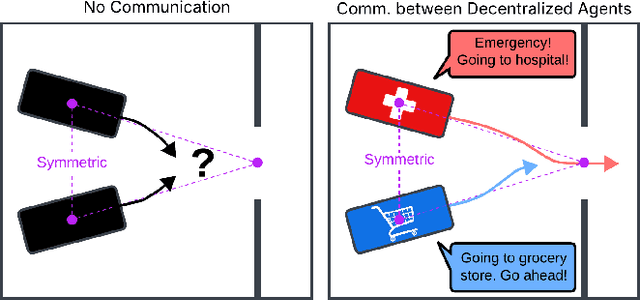
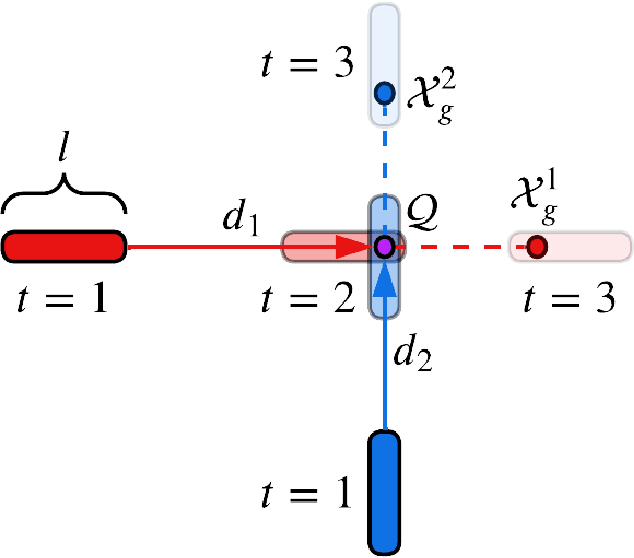
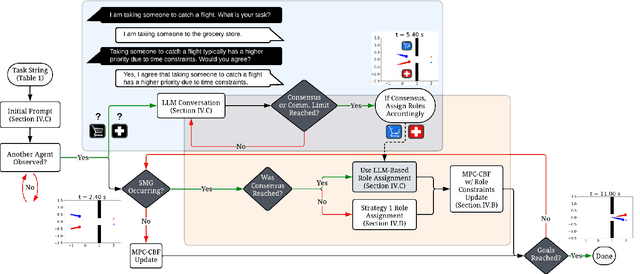
Safe, agile, and socially compliant multi-robot navigation in cluttered and constrained environments remains a critical challenge. This is especially difficult with self-interested agents in decentralized settings, where there is no central authority to resolve conflicts induced by spatial symmetry. We address this challenge by proposing a novel approach, GameChat, which facilitates safe, agile, and deadlock-free navigation for both cooperative and self-interested agents. Key to our approach is the use of natural language communication to resolve conflicts, enabling agents to prioritize more urgent tasks and break spatial symmetry in a socially optimal manner. Our algorithm ensures subgame perfect equilibrium, preventing agents from deviating from agreed-upon behaviors and supporting cooperation. Furthermore, we guarantee safety through control barrier functions and preserve agility by minimizing disruptions to agents' planned trajectories. We evaluate GameChat in simulated environments with doorways and intersections. The results show that even in the worst case, GameChat reduces the time for all agents to reach their goals by over 35% from a naive baseline and by over 20% from SMG-CBF in the intersection scenario, while doubling the rate of ensuring the agent with a higher priority task reaches the goal first, from 50% (equivalent to random chance) to a 100% perfect performance at maximizing social welfare.

Group Fairness in Multi-Task Reinforcement Learning

This paper addresses a critical societal consideration in the application of Reinforcement Learning (RL): ensuring equitable outcomes across different demographic groups in multi-task settings. While previous work has explored fairness in single-task RL, many real-world applications are multi-task in nature and require policies to maintain fairness across all tasks. We introduce a novel formulation of multi-task group fairness in RL and propose a constrained optimization algorithm that explicitly enforces fairness constraints across multiple tasks simultaneously. We have shown that our proposed algorithm does not violate fairness constraints with high probability and with sublinear regret in the finite-horizon episodic setting. Through experiments in RiverSwim and MuJoCo environments, we demonstrate that our approach better ensures group fairness across multiple tasks compared to previous methods that lack explicit multi-task fairness constraints in both the finite-horizon setting and the infinite-horizon setting. Our results show that the proposed algorithm achieves smaller fairness gaps while maintaining comparable returns across different demographic groups and tasks, suggesting its potential for addressing fairness concerns in real-world multi-task RL applications.

Towards Large Language Models that Benefit for All: Benchmarking Group Fairness in Reward Models

As Large Language Models (LLMs) become increasingly powerful and accessible to human users, ensuring fairness across diverse demographic groups, i.e., group fairness, is a critical ethical concern. However, current fairness and bias research in LLMs is limited in two aspects. First, compared to traditional group fairness in machine learning classification, it requires that the non-sensitive attributes, in this case, the prompt questions, be the same across different groups. In many practical scenarios, different groups, however, may prefer different prompt questions and this requirement becomes impractical. Second, it evaluates group fairness only for the LLM's final output without identifying the source of possible bias. Namely, the bias in LLM's output can result from both the pretraining and the finetuning. For finetuning, the bias can result from both the RLHF procedure and the learned reward model. Arguably, evaluating the group fairness of each component in the LLM pipeline could help develop better methods to mitigate the possible bias. Recognizing those two limitations, this work benchmarks the group fairness of learned reward models. By using expert-written text from arXiv, we are able to benchmark the group fairness of reward models without requiring the same prompt questions across different demographic groups. Surprisingly, our results demonstrate that all the evaluated reward models (e.g., Nemotron-4-340B-Reward, ArmoRM-Llama3-8B-v0.1, and GRM-llama3-8B-sftreg) exhibit statistically significant group unfairness. We also observed that top-performing reward models (w.r.t. canonical performance metrics) tend to demonstrate better group fairness.

A Survey of In-Context Reinforcement Learning

Reinforcement learning (RL) agents typically optimize their policies by performing expensive backward passes to update their network parameters. However, some agents can solve new tasks without updating any parameters by simply conditioning on additional context such as their action-observation histories. This paper surveys work on such behavior, known as in-context reinforcement learning.

Linear $Q$-Learning Does Not Diverge: Convergence Rates to a Bounded Set

$Q$-learning is one of the most fundamental reinforcement learning algorithms. Previously, it is widely believed that $Q$-learning with linear function approximation (i.e., linear $Q$-learning) suffers from possible divergence. This paper instead establishes the first $L^2$ convergence rate of linear $Q$-learning to a bounded set. Notably, we do not make any modification to the original linear $Q$-learning algorithm, do not make any Bellman completeness assumption, and do not make any near-optimality assumption on the behavior policy. All we need is an $\epsilon$-softmax behavior policy with an adaptive temperature. The key to our analysis is the general result of stochastic approximations under Markovian noise with fast-changing transition functions. As a side product, we also use this general result to establish the $L^2$ convergence rate of tabular $Q$-learning with an $\epsilon$-softmax behavior policy, for which we rely on a novel pseudo-contraction property of the weighted Bellman optimality operator.

CRASH: Challenging Reinforcement-Learning Based Adversarial Scenarios For Safety Hardening

Ensuring the safety of autonomous vehicles (AVs) requires identifying rare but critical failure cases that on-road testing alone cannot discover. High-fidelity simulations provide a scalable alternative, but automatically generating realistic and diverse traffic scenarios that can effectively stress test AV motion planners remains a key challenge. This paper introduces CRASH - Challenging Reinforcement-learning based Adversarial scenarios for Safety Hardening - an adversarial deep reinforcement learning framework to address this issue. First CRASH can control adversarial Non Player Character (NPC) agents in an AV simulator to automatically induce collisions with the Ego vehicle, falsifying its motion planner. We also propose a novel approach, that we term safety hardening, which iteratively refines the motion planner by simulating improvement scenarios against adversarial agents, leveraging the failure cases to strengthen the AV stack. CRASH is evaluated on a simplified two-lane highway scenario, demonstrating its ability to falsify both rule-based and learning-based planners with collision rates exceeding 90%. Additionally, safety hardening reduces the Ego vehicle's collision rate by 26%. While preliminary, these results highlight RL-based safety hardening as a promising approach for scenario-driven simulation testing for autonomous vehicles.

Almost Sure Convergence Rates and Concentration of Stochastic Approximation and Reinforcement Learning with Markovian Noise

This paper establishes the first almost sure convergence rate and the first maximal concentration bound with exponential tails for general contractive stochastic approximation algorithms with Markovian noise. As a corollary, we also obtain convergence rates in $L^p$. Key to our successes is a novel discretization of the mean ODE of stochastic approximation algorithms using intervals with diminishing (instead of constant) length. As applications, we provide the first almost sure convergence rate for $Q$-learning with Markovian samples without count-based learning rates. We also provide the first concentration bound for off-policy temporal difference learning with Markovian samples.

Efficient Policy Evaluation with Safety Constraint for Reinforcement Learning

In reinforcement learning, classic on-policy evaluation methods often suffer from high variance and require massive online data to attain the desired accuracy. Previous studies attempt to reduce evaluation variance by searching for or designing proper behavior policies to collect data. However, these approaches ignore the safety of such behavior policies -- the designed behavior policies have no safety guarantee and may lead to severe damage during online executions. In this paper, to address the challenge of reducing variance while ensuring safety simultaneously, we propose an optimal variance-minimizing behavior policy under safety constraints. Theoretically, while ensuring safety constraints, our evaluation method is unbiased and has lower variance than on-policy evaluation. Empirically, our method is the only existing method to achieve both substantial variance reduction and safety constraint satisfaction. Furthermore, we show our method is even superior to previous methods in both variance reduction and execution safety.

Doubly Optimal Policy Evaluation for Reinforcement Learning

Policy evaluation estimates the performance of a policy by (1) collecting data from the environment and (2) processing raw data into a meaningful estimate. Due to the sequential nature of reinforcement learning, any improper data-collecting policy or data-processing method substantially deteriorates the variance of evaluation results over long time steps. Thus, policy evaluation often suffers from large variance and requires massive data to achieve the desired accuracy. In this work, we design an optimal combination of data-collecting policy and data-processing baseline. Theoretically, we prove our doubly optimal policy evaluation method is unbiased and guaranteed to have lower variance than previously best-performing methods. Empirically, compared with previous works, we show our method reduces variance substantially and achieves superior empirical performance.