Experience Replay Addresses Loss of Plasticity in Continual Learning

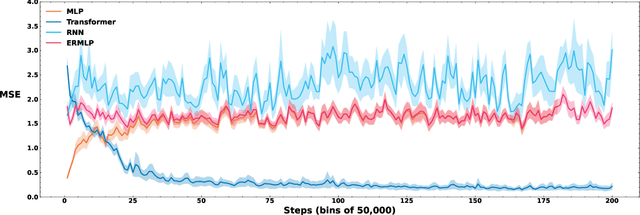
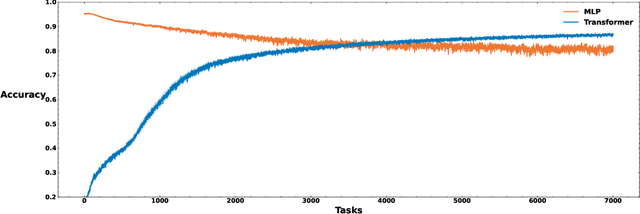
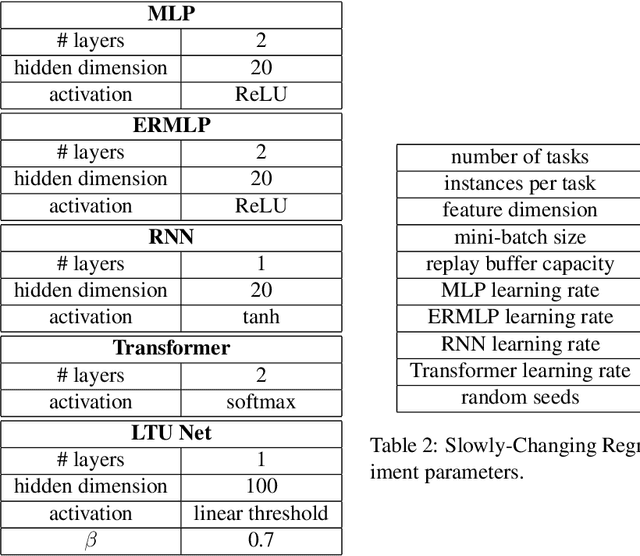
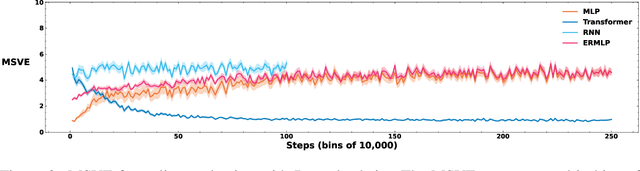
Loss of plasticity is one of the main challenges in continual learning with deep neural networks, where neural networks trained via backpropagation gradually lose their ability to adapt to new tasks and perform significantly worse than their freshly initialized counterparts. The main contribution of this paper is to propose a new hypothesis that experience replay addresses the loss of plasticity in continual learning. Here, experience replay is a form of memory. We provide supporting evidence for this hypothesis. In particular, we demonstrate in multiple different tasks, including regression, classification, and policy evaluation, that by simply adding an experience replay and processing the data in the experience replay with Transformers, the loss of plasticity disappears. Notably, we do not alter any standard components of deep learning. For example, we do not change backpropagation. We do not modify the activation functions. And we do not use any regularization. We conjecture that experience replay and Transformers can address the loss of plasticity because of the in-context learning phenomenon.

A Survey of In-Context Reinforcement Learning

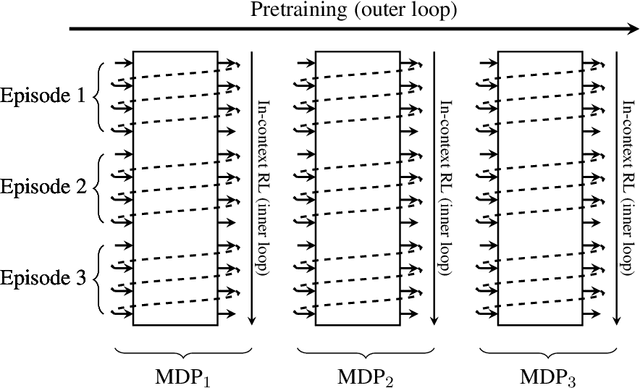
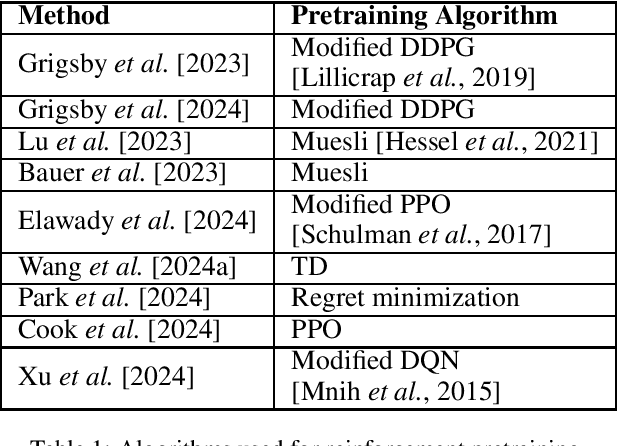
Reinforcement learning (RL) agents typically optimize their policies by performing expensive backward passes to update their network parameters. However, some agents can solve new tasks without updating any parameters by simply conditioning on additional context such as their action-observation histories. This paper surveys work on such behavior, known as in-context reinforcement learning.

Almost Sure Convergence of Linear Temporal Difference Learning with Arbitrary Features

Temporal difference (TD) learning with linear function approximation, abbreviated as linear TD, is a classic and powerful prediction algorithm in reinforcement learning. While it is well understood that linear TD converges almost surely to a unique point, this convergence traditionally requires the assumption that the features used by the approximator are linearly independent. However, this linear independence assumption does not hold in many practical scenarios. This work is the first to establish the almost sure convergence of linear TD without requiring linearly independent features. In fact, we do not make any assumptions on the features. We prove that the approximated value function converges to a unique point and the weight iterates converge to a set. We also establish a notion of local stability of the weight iterates. Importantly, we do not need to introduce any other additional assumptions and do not need to make any modification to the linear TD algorithm. Key to our analysis is a novel characterization of bounded invariant sets of the mean ODE of linear TD.

Transformers Learn Temporal Difference Methods for In-Context Reinforcement Learning

In-context learning refers to the learning ability of a model during inference time without adapting its parameters. The input (i.e., prompt) to the model (e.g., transformers) consists of both a context (i.e., instance-label pairs) and a query instance. The model is then able to output a label for the query instance according to the context during inference. A possible explanation for in-context learning is that the forward pass of (linear) transformers implements iterations of gradient descent on the instance-label pairs in the context. In this paper, we prove by construction that transformers can also implement temporal difference (TD) learning in the forward pass, a phenomenon we refer to as in-context TD. We demonstrate the emergence of in-context TD after training the transformer with a multi-task TD algorithm, accompanied by theoretical analysis. Furthermore, we prove that transformers are expressive enough to implement many other policy evaluation algorithms in the forward pass, including residual gradient, TD with eligibility trace, and average-reward TD.