Provable optimal transport with transformers: The essence of depth and prompt engineering

Can we establish provable performance guarantees for transformers? Establishing such theoretical guarantees is a milestone in developing trustworthy generative AI. In this paper, we take a step toward addressing this question by focusing on optimal transport, a fundamental problem at the intersection of combinatorial and continuous optimization. Leveraging the computational power of attention layers, we prove that a transformer with fixed parameters can effectively solve the optimal transport problem in Wasserstein-2 with entropic regularization for an arbitrary number of points. Consequently, the transformer can sort lists of arbitrary sizes up to an approximation factor. Our results rely on an engineered prompt that enables the transformer to implement gradient descent with adaptive stepsizes on the dual optimal transport. Combining the convergence analysis of gradient descent with Sinkhorn dynamics, we establish an explicit approximation bound for optimal transport with transformers, which improves as depth increases. Our findings provide novel insights into the essence of prompt engineering and depth for solving optimal transport. In particular, prompt engineering boosts the algorithmic expressivity of transformers, allowing them implement an optimization method. With increasing depth, transformers can simulate several iterations of gradient descent.

Transformers Learn Temporal Difference Methods for In-Context Reinforcement Learning

In-context learning refers to the learning ability of a model during inference time without adapting its parameters. The input (i.e., prompt) to the model (e.g., transformers) consists of both a context (i.e., instance-label pairs) and a query instance. The model is then able to output a label for the query instance according to the context during inference. A possible explanation for in-context learning is that the forward pass of (linear) transformers implements iterations of gradient descent on the instance-label pairs in the context. In this paper, we prove by construction that transformers can also implement temporal difference (TD) learning in the forward pass, a phenomenon we refer to as in-context TD. We demonstrate the emergence of in-context TD after training the transformer with a multi-task TD algorithm, accompanied by theoretical analysis. Furthermore, we prove that transformers are expressive enough to implement many other policy evaluation algorithms in the forward pass, including residual gradient, TD with eligibility trace, and average-reward TD.

Towards Training Without Depth Limits: Batch Normalization Without Gradient Explosion

Normalization layers are one of the key building blocks for deep neural networks. Several theoretical studies have shown that batch normalization improves the signal propagation, by avoiding the representations from becoming collinear across the layers. However, results on mean-field theory of batch normalization also conclude that this benefit comes at the expense of exploding gradients in depth. Motivated by these two aspects of batch normalization, in this study we pose the following question: "Can a batch-normalized network keep the optimal signal propagation properties, but avoid exploding gradients?" We answer this question in the affirmative by giving a particular construction of an Multi-Layer Perceptron (MLP) with linear activations and batch-normalization that provably has bounded gradients at any depth. Based on Weingarten calculus, we develop a rigorous and non-asymptotic theory for this constructed MLP that gives a precise characterization of forward signal propagation, while proving that gradients remain bounded for linearly independent input samples, which holds in most practical settings. Inspired by our theory, we also design an activation shaping scheme that empirically achieves the same properties for certain non-linear activations.

Transformers learn to implement preconditioned gradient descent for in-context learning

Motivated by the striking ability of transformers for in-context learning, several works demonstrate that transformers can implement algorithms like gradient descent. By a careful construction of weights, these works show that multiple layers of transformers are expressive enough to simulate gradient descent iterations. Going beyond the question of expressivity, we ask: Can transformers learn to implement such algorithms by training over random problem instances? To our knowledge, we make the first theoretical progress toward this question via analysis of the loss landscape for linear transformers trained over random instances of linear regression. For a single attention layer, we prove the global minimum of the training objective implements a single iteration of preconditioned gradient descent. Notably, the preconditioning matrix not only adapts to the input distribution but also to the variance induced by data inadequacy. For a transformer with $k$ attention layers, we prove certain critical points of the training objective implement $k$ iterations of preconditioned gradient descent. Our results call for future theoretical studies on learning algorithms by training transformers.

On the impact of activation and normalization in obtaining isometric embeddings at initialization

In this paper, we explore the structure of the penultimate Gram matrix in deep neural networks, which contains the pairwise inner products of outputs corresponding to a batch of inputs. In several architectures it has been observed that this Gram matrix becomes degenerate with depth at initialization, which dramatically slows training. Normalization layers, such as batch or layer normalization, play a pivotal role in preventing the rank collapse issue. Despite promising advances, the existing theoretical results (i) do not extend to layer normalization, which is widely used in transformers, (ii) can not characterize the bias of normalization quantitatively at finite depth. To bridge this gap, we provide a proof that layer normalization, in conjunction with activation layers, biases the Gram matrix of a multilayer perceptron towards isometry at an exponential rate with depth at initialization. We quantify this rate using the Hermite expansion of the activation function, highlighting the importance of higher order ($\ge 2$) Hermite coefficients in the bias towards isometry.

Efficient displacement convex optimization with particle gradient descent

Particle gradient descent, which uses particles to represent a probability measure and performs gradient descent on particles in parallel, is widely used to optimize functions of probability measures. This paper considers particle gradient descent with a finite number of particles and establishes its theoretical guarantees to optimize functions that are \emph{displacement convex} in measures. Concretely, for Lipschitz displacement convex functions defined on probability over $\mathbb{R}^d$, we prove that $O(1/\epsilon^2)$ particles and $O(d/\epsilon^4)$ computations are sufficient to find the $\epsilon$-optimal solutions. We further provide improved complexity bounds for optimizing smooth displacement convex functions. We demonstrate the application of our results for function approximation with specific neural architectures with two-dimensional inputs.

Entropy Maximization with Depth: A Variational Principle for Random Neural Networks

To understand the essential role of depth in neural networks, we investigate a variational principle for depth: Does increasing depth perform an implicit optimization for the representations in neural networks? We prove that random neural networks equipped with batch normalization maximize the differential entropy of representations with depth up to constant factors, assuming that the representations are contractive. Thus, representations inherently obey the \textit{principle of maximum entropy} at initialization, in the absence of information about the learning task. Our variational formulation for neural representations characterizes the interplay between representation entropy and architectural components, including depth, width, and non-linear activations, thereby potentially inspiring the design of neural architectures.

Polynomial-time sparse measure recovery

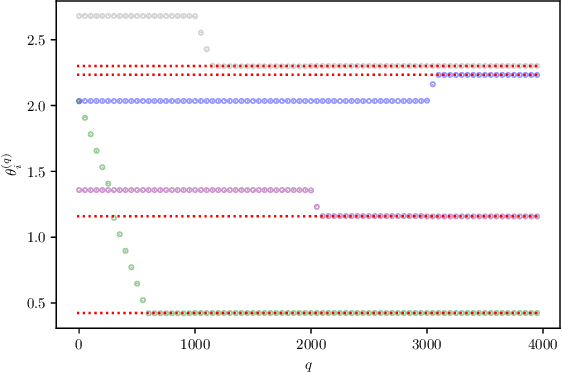
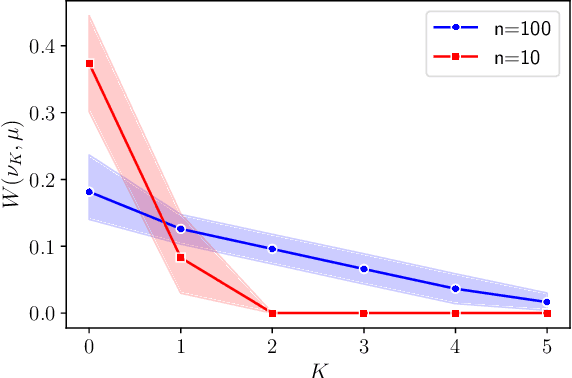
How to recover a probability measure with sparse support from particular moments? This problem has been the focus of research in theoretical computer science and neural computing. However, there is no polynomial-time algorithm for the recovery. The best algorithm for the recovery requires $O(2^{\text{poly}(1/\epsilon)})$ for $\epsilon$-accurate recovery. We propose the first poly-time recovery method from carefully designed moments that only requires $O(\log(1/\epsilon)/\epsilon^2)$ computations for an $\epsilon$-accurate recovery. This method relies on the recovery of a planted two-layer neural network with two-dimensional inputs, a finite width, and zero-one activation. For such networks, we establish the first global convergence of gradient descent and demonstrate its application in sparse measure recovery.

Batch Normalization Orthogonalizes Representations in Deep Random Networks

This paper underlines a subtle property of batch-normalization (BN): Successive batch normalizations with random linear transformations make hidden representations increasingly orthogonal across layers of a deep neural network. We establish a non-asymptotic characterization of the interplay between depth, width, and the orthogonality of deep representations. More precisely, under a mild assumption, we prove that the deviation of the representations from orthogonality rapidly decays with depth up to a term inversely proportional to the network width. This result has two main implications: 1) Theoretically, as the depth grows, the distribution of the representation -- after the linear layers -- contracts to a Wasserstein-2 ball around an isotropic Gaussian distribution. Furthermore, the radius of this Wasserstein ball shrinks with the width of the network. 2) In practice, the orthogonality of the representations directly influences the performance of stochastic gradient descent (SGD). When representations are initially aligned, we observe SGD wastes many iterations to orthogonalize representations before the classification. Nevertheless, we experimentally show that starting optimization from orthogonal representations is sufficient to accelerate SGD, with no need for BN.

Revisiting the Role of Euler Numerical Integration on Acceleration and Stability in Convex Optimization

Viewing optimization methods as numerical integrators for ordinary differential equations (ODEs) provides a thought-provoking modern framework for studying accelerated first-order optimizers. In this literature, acceleration is often supposed to be linked to the quality of the integrator (accuracy, energy preservation, symplecticity). In this work, we propose a novel ordinary differential equation that questions this connection: both the explicit and the semi-implicit (a.k.a symplectic) Euler discretizations on this ODE lead to an accelerated algorithm for convex programming. Although semi-implicit methods are well-known in numerical analysis to enjoy many desirable features for the integration of physical systems, our findings show that these properties do not necessarily relate to acceleration.