Almost Sure Convergence of Average Reward Temporal Difference Learning

Tabular average reward Temporal Difference (TD) learning is perhaps the simplest and the most fundamental policy evaluation algorithm in average reward reinforcement learning. After at least 25 years since its discovery, we are finally able to provide a long-awaited almost sure convergence analysis. Namely, we are the first to prove that, under very mild conditions, tabular average reward TD converges almost surely to a sample path dependent fixed point. Key to this success is a new general stochastic approximation result concerning nonexpansive mappings with Markovian and additive noise, built on recent advances in stochastic Krasnoselskii-Mann iterations.

Transformers Learn Temporal Difference Methods for In-Context Reinforcement Learning

In-context learning refers to the learning ability of a model during inference time without adapting its parameters. The input (i.e., prompt) to the model (e.g., transformers) consists of both a context (i.e., instance-label pairs) and a query instance. The model is then able to output a label for the query instance according to the context during inference. A possible explanation for in-context learning is that the forward pass of (linear) transformers implements iterations of gradient descent on the instance-label pairs in the context. In this paper, we prove by construction that transformers can also implement temporal difference (TD) learning in the forward pass, a phenomenon we refer to as in-context TD. We demonstrate the emergence of in-context TD after training the transformer with a multi-task TD algorithm, accompanied by theoretical analysis. Furthermore, we prove that transformers are expressive enough to implement many other policy evaluation algorithms in the forward pass, including residual gradient, TD with eligibility trace, and average-reward TD.

Federated Linear Contextual Bandits with Heterogeneous Clients

The demand for collaborative and private bandit learning across multiple agents is surging due to the growing quantity of data generated from distributed systems. Federated bandit learning has emerged as a promising framework for private, efficient, and decentralized online learning. However, almost all previous works rely on strong assumptions of client homogeneity, i.e., all participating clients shall share the same bandit model; otherwise, they all would suffer linear regret. This greatly restricts the application of federated bandit learning in practice. In this work, we introduce a new approach for federated bandits for heterogeneous clients, which clusters clients for collaborative bandit learning under the federated learning setting. Our proposed algorithm achieves non-trivial sub-linear regret and communication cost for all clients, subject to the communication protocol under federated learning that at anytime only one model can be shared by the server.

Graph Structural Attack by Spectral Distance

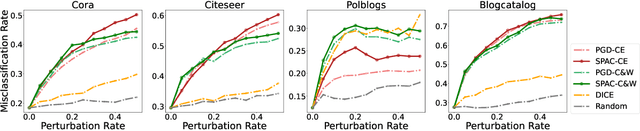
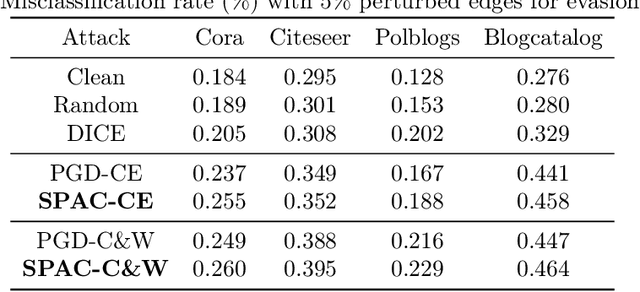
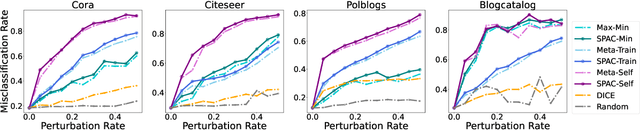
Graph Convolutional Networks (GCNs) have fueled a surge of interest due to their superior performance on graph learning tasks, but are also shown vulnerability to adversarial attacks. In this paper, an effective graph structural attack is investigated to disrupt graph spectral filters in the Fourier domain. We define the spectral distance based on the eigenvalues of graph Laplacian to measure the disruption of spectral filters. We then generate edge perturbations by simultaneously maximizing a task-specific attack objective and the proposed spectral distance. The experiments demonstrate remarkable effectiveness of the proposed attack in the white-box setting at both training and test time. Our qualitative analysis shows the connection between the attack behavior and the imposed changes on the spectral distribution, which provides empirical evidence that maximizing spectral distance is an effective manner to change the structural property of graphs in the spatial domain and perturb the frequency components in the Fourier domain.

Graph Embedding with Hierarchical Attentive Membership

The exploitation of graph structures is the key to effectively learning representations of nodes that preserve useful information in graphs. A remarkable property of graph is that a latent hierarchical grouping of nodes exists in a global perspective, where each node manifests its membership to a specific group based on the context composed by its neighboring nodes. Most prior works ignore such latent groups and nodes' membership to different groups, not to mention the hierarchy, when modeling the neighborhood structure. Thus, they fall short of delivering a comprehensive understanding of the nodes under different contexts in a graph. In this paper, we propose a novel hierarchical attentive membership model for graph embedding, where the latent memberships for each node are dynamically discovered based on its neighboring context. Both group-level and individual-level attentions are performed when aggregating neighboring states to generate node embeddings. We introduce structural constraints to explicitly regularize the inferred memberships of each node, such that a well-defined hierarchical grouping structure is captured. The proposed model outperformed a set of state-of-the-art graph embedding solutions on node classification and link prediction tasks in a variety of graphs including citation networks and social networks. Qualitative evaluations visualize the learned node embeddings along with the inferred memberships, which proved the concept of membership hierarchy and enables explainable embedding learning in graphs.