Graph Structural Attack by Spectral Distance
Paper and Code
Nov 03, 2021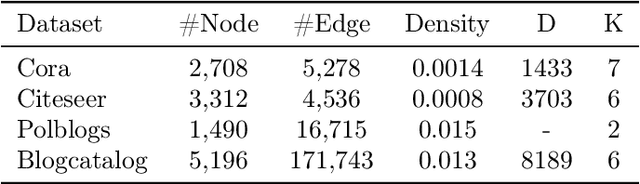
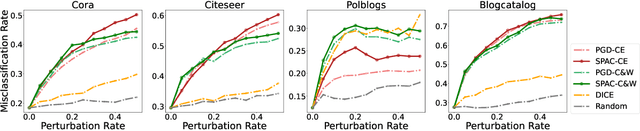
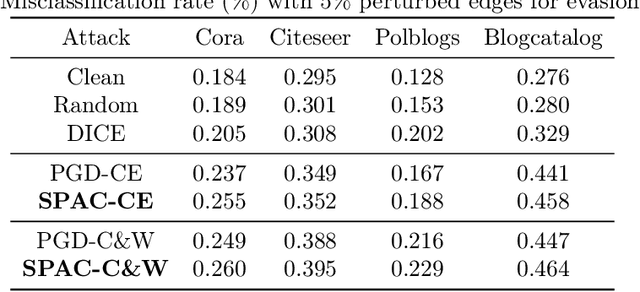
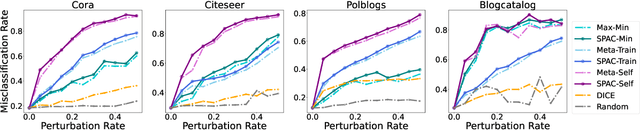
Graph Convolutional Networks (GCNs) have fueled a surge of interest due to their superior performance on graph learning tasks, but are also shown vulnerability to adversarial attacks. In this paper, an effective graph structural attack is investigated to disrupt graph spectral filters in the Fourier domain. We define the spectral distance based on the eigenvalues of graph Laplacian to measure the disruption of spectral filters. We then generate edge perturbations by simultaneously maximizing a task-specific attack objective and the proposed spectral distance. The experiments demonstrate remarkable effectiveness of the proposed attack in the white-box setting at both training and test time. Our qualitative analysis shows the connection between the attack behavior and the imposed changes on the spectral distribution, which provides empirical evidence that maximizing spectral distance is an effective manner to change the structural property of graphs in the spatial domain and perturb the frequency components in the Fourier domain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge