Efficient Policy Evaluation with Safety Constraint for Reinforcement Learning

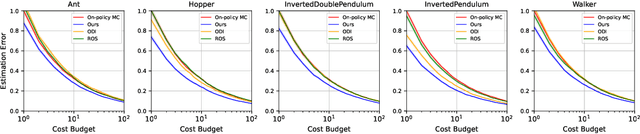
In reinforcement learning, classic on-policy evaluation methods often suffer from high variance and require massive online data to attain the desired accuracy. Previous studies attempt to reduce evaluation variance by searching for or designing proper behavior policies to collect data. However, these approaches ignore the safety of such behavior policies -- the designed behavior policies have no safety guarantee and may lead to severe damage during online executions. In this paper, to address the challenge of reducing variance while ensuring safety simultaneously, we propose an optimal variance-minimizing behavior policy under safety constraints. Theoretically, while ensuring safety constraints, our evaluation method is unbiased and has lower variance than on-policy evaluation. Empirically, our method is the only existing method to achieve both substantial variance reduction and safety constraint satisfaction. Furthermore, we show our method is even superior to previous methods in both variance reduction and execution safety.

Doubly Optimal Policy Evaluation for Reinforcement Learning

Policy evaluation estimates the performance of a policy by (1) collecting data from the environment and (2) processing raw data into a meaningful estimate. Due to the sequential nature of reinforcement learning, any improper data-collecting policy or data-processing method substantially deteriorates the variance of evaluation results over long time steps. Thus, policy evaluation often suffers from large variance and requires massive data to achieve the desired accuracy. In this work, we design an optimal combination of data-collecting policy and data-processing baseline. Theoretically, we prove our doubly optimal policy evaluation method is unbiased and guaranteed to have lower variance than previously best-performing methods. Empirically, compared with previous works, we show our method reduces variance substantially and achieves superior empirical performance.

Efficient Multi-Policy Evaluation for Reinforcement Learning

To unbiasedly evaluate multiple target policies, the dominant approach among RL practitioners is to run and evaluate each target policy separately. However, this evaluation method is far from efficient because samples are not shared across policies, and running target policies to evaluate themselves is actually not optimal. In this paper, we address these two weaknesses by designing a tailored behavior policy to reduce the variance of estimators across all target policies. Theoretically, we prove that executing this behavior policy with manyfold fewer samples outperforms on-policy evaluation on every target policy under characterized conditions. Empirically, we show our estimator has a substantially lower variance compared with previous best methods and achieves state-of-the-art performance in a broad range of environments.

The ODE Method for Stochastic Approximation and Reinforcement Learning with Markovian Noise

Stochastic approximation is a class of algorithms that update a vector iteratively, incrementally, and stochastically, including, e.g., stochastic gradient descent and temporal difference learning. One fundamental challenge in analyzing a stochastic approximation algorithm is to establish its stability, i.e., to show that the stochastic vector iterates are bounded almost surely. In this paper, we extend the celebrated Borkar-Meyn theorem for stability from the Martingale difference noise setting to the Markovian noise setting, which greatly improves its applicability in reinforcement learning, especially in those off-policy reinforcement learning algorithms with linear function approximation and eligibility traces. Central to our analysis is the diminishing asymptotic rate of change of a few functions, which is implied by both a form of strong law of large numbers and a commonly used V4 Lyapunov drift condition and trivially holds if the Markov chain is finite and irreducible.

Improving Monte Carlo Evaluation with Offline Data

Monte Carlo (MC) methods are the most widely used methods to estimate the performance of a policy. Given an interested policy, MC methods give estimates by repeatedly running this policy to collect samples and taking the average of the outcomes. Samples collected during this process are called online samples. To get an accurate estimate, MC methods consume massive online samples. When online samples are expensive, e.g., online recommendations and inventory management, we want to reduce the number of online samples while achieving the same estimate accuracy. To this end, we use off-policy MC methods that evaluate the interested policy by running a different policy called behavior policy. We design a tailored behavior policy such that the variance of the off-policy MC estimator is provably smaller than the ordinary MC estimator. Importantly, this tailored behavior policy can be efficiently learned from existing offline data, i,e., previously logged data, which are much cheaper than online samples. With reduced variance, our off-policy MC method requires fewer online samples to evaluate the performance of a policy compared with the ordinary MC method. Moreover, our off-policy MC estimator is always unbiased.