The Bayesian Context Trees State Space Model for time series modelling and forecasting

A hierarchical Bayesian framework is introduced for developing rich mixture models for real-valued time series, along with a collection of effective tools for learning and inference. At the top level, meaningful discrete states are identified as appropriately quantised values of some of the most recent samples. This collection of observable states is described as a discrete context-tree model. Then, at the bottom level, a different, arbitrary model for real-valued time series - a base model - is associated with each state. This defines a very general framework that can be used in conjunction with any existing model class to build flexible and interpretable mixture models. We call this the Bayesian Context Trees State Space Model, or the BCT-X framework. Efficient algorithms are introduced that allow for effective, exact Bayesian inference; in particular, the maximum a posteriori probability (MAP) context-tree model can be identified. These algorithms can be updated sequentially, facilitating efficient online forecasting. The utility of the general framework is illustrated in two particular instances: When autoregressive (AR) models are used as base models, resulting in a nonlinear AR mixture model, and when conditional heteroscedastic (ARCH) models are used, resulting in a mixture model that offers a powerful and systematic way of modelling the well-known volatility asymmetries in financial data. In forecasting, the BCT-X methods are found to outperform state-of-the-art techniques on simulated and real-world data, both in terms of accuracy and computational requirements. In modelling, the BCT-X structure finds natural structure present in the data. In particular, the BCT-ARCH model reveals a novel, important feature of stock market index data, in the form of an enhanced leverage effect.

Change-point Detection and Segmentation of Discrete Data using Bayesian Context Trees

A new Bayesian modelling framework is introduced for piece-wise homogeneous variable-memory Markov chains, along with a collection of effective algorithmic tools for change-point detection and segmentation of discrete time series. Building on the recently introduced Bayesian Context Trees (BCT) framework, the distributions of different segments in a discrete time series are described as variable-memory Markov chains. Inference for the presence and location of change-points is then performed via Markov chain Monte Carlo sampling. The key observation that facilitates effective sampling is that, using one of the BCT algorithms, the prior predictive likelihood of the data can be computed exactly, integrating out all the models and parameters in each segment. This makes it possible to sample directly from the posterior distribution of the number and location of the change-points, leading to accurate estimates and providing a natural quantitative measure of uncertainty in the results. Estimates of the actual model in each segment can also be obtained, at essentially no additional computational cost. Results on both simulated and real-world data indicate that the proposed methodology performs better than or as well as state-of-the-art techniques.

The ODE Method for Asymptotic Statistics in Stochastic Approximation and Reinforcement Learning

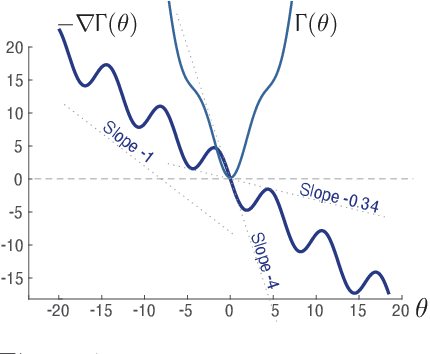
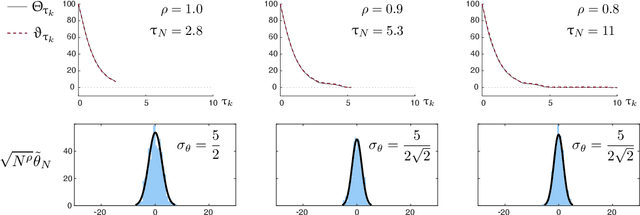
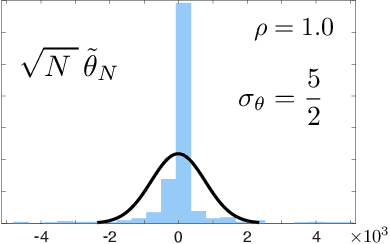
The paper concerns convergence and asymptotic statistics for stochastic approximation driven by Markovian noise: $$ \theta_{n+1}= \theta_n + \alpha_{n + 1} f(\theta_n, \Phi_{n+1}) \,,\quad n\ge 0, $$ in which each $\theta_n\in\Re^d$, $ \{ \Phi_n \}$ is a Markov chain on a general state space X with stationary distribution $\pi$, and $f:\Re^d\times \text{X} \to\Re^d$. In addition to standard Lipschitz bounds on $f$, and conditions on the vanishing step-size sequence $\{\alpha_n\}$, it is assumed that the associated ODE is globally asymptotically stable with stationary point denoted $\theta^*$, where $\bar f(\theta)=E[f(\theta,\Phi)]$ with $\Phi\sim\pi$. Moreover, the ODE@$\infty$ defined with respect to the vector field, $$ \bar f_\infty(\theta):= \lim_{r\to\infty} r^{-1} \bar f(r\theta) \,,\qquad \theta\in\Re^d, $$ is asymptotically stable. The main contributions are summarized as follows: (i) The sequence $\theta$ is convergent if $\Phi$ is geometrically ergodic, and subject to compatible bounds on $f$. The remaining results are established under a stronger assumption on the Markov chain: A slightly weaker version of the Donsker-Varadhan Lyapunov drift condition known as (DV3). (ii) A Lyapunov function is constructed for the joint process $\{\theta_n,\Phi_n\}$ that implies convergence of $\{ \theta_n\}$ in $L_4$. (iii) A functional CLT is established, as well as the usual one-dimensional CLT for the normalized error $z_n:= (\theta_n-\theta^*)/\sqrt{\alpha_n}$. Moment bounds combined with the CLT imply convergence of the normalized covariance, $$ \lim_{n \to \infty} E [ z_n z_n^T ] = \Sigma_\theta, $$ where $\Sigma_\theta$ is the asymptotic covariance appearing in the CLT. (iv) An example is provided where the Markov chain $\Phi$ is geometrically ergodic but it does not satisfy (DV3). While the algorithm is convergent, the second moment is unbounded.

Hierarchical Bayesian Mixture Models for Time Series Using Context Trees as State Space Partitions

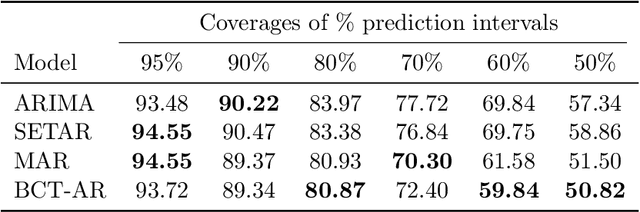
A general Bayesian framework is introduced for mixture modelling and inference with real-valued time series. At the top level, the state space is partitioned via the choice of a discrete context tree, so that the resulting partition depends on the values of some of the most recent samples. At the bottom level, a different model is associated with each region of the partition. This defines a very rich and flexible class of mixture models, for which we provide algorithms that allow for efficient, exact Bayesian inference. In particular, we show that the maximum a posteriori probability (MAP) model (including the relevant MAP context tree partition) can be precisely identified, along with its exact posterior probability. The utility of this general framework is illustrated in detail when a different autoregressive (AR) model is used in each state-space region, resulting in a mixture-of-AR model class. The performance of the associated algorithmic tools is demonstrated in the problems of model selection and forecasting on both simulated and real-world data, where they are found to provide results as good or better than state-of-the-art methods.

Inferring community characteristics in labelled networks

Labelled networks form a very common and important class of data, naturally appearing in numerous applications in science and engineering. A typical inference goal is to determine how the vertex labels(or {\em features}) affect the network's graph structure. A standard approach has been to partition the network into blocks grouped by distinct values of the feature of interest. A block-based random graph model -- typically a variant of the stochastic block model -- is then used to test for evidence of asymmetric behaviour within these feature-based communities. Nevertheless, the resulting communities often do not produce a natural partition of the graph. In this work, we introduce a new generative model, the feature-first block model (FFBM), which is more effective at describing vertex-labelled undirected graphs and also facilitates the use of richer queries on labelled networks. We develop a Bayesian framework for inference with this model, and we present a method to efficiently sample from the posterior distribution of the FFBM parameters. The FFBM's structure is kept deliberately simple to retain easy interpretability of the parameter values. We apply the proposed methods to a variety of network data to extract the most important features along which the vertices are partitioned. The main advantages of the proposed approach are that the whole feature-space is used automatically, and features can be rank-ordered implicitly according to impact. Any features that do not significantly impact the high-level structure can be discarded to reduce the problem dimension. In cases where the vertex features available do not readily explain the community structure in the resulting network, the approach detects this and is protected against over-fitting. Results on several real-world datasets illustrate the performance of the proposed methods.

Optimal rates for independence testing via $U$-statistic permutation tests

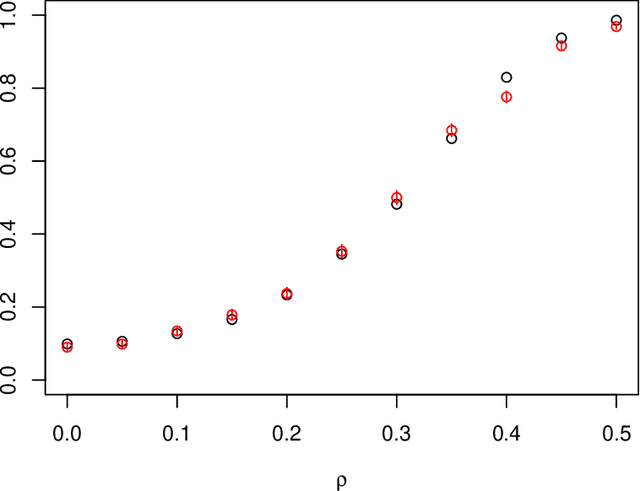
We study the problem of independence testing given independent and identically distributed pairs taking values in a $\sigma$-finite, separable measure space. Defining a natural measure of dependence $D(f)$ as the squared $L_2$-distance between a joint density $f$ and the product of its marginals, we first show that there is no valid test of independence that is uniformly consistent against alternatives of the form $\{f: D(f) \geq \rho^2 \}$. We therefore restrict attention to alternatives that impose additional Sobolev-type smoothness constraints, and define a permutation test based on a basis expansion and a $U$-statistic estimator of $D(f)$ that we prove is minimax optimal in terms of its separation rates in many instances. Finally, for the case of a Fourier basis on $[0,1]^2$, we provide an approximation to the power function that offers several additional insights.

Differential Temporal Difference Learning

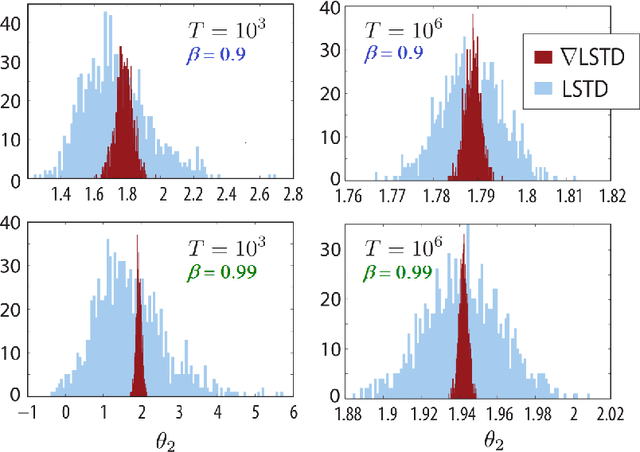
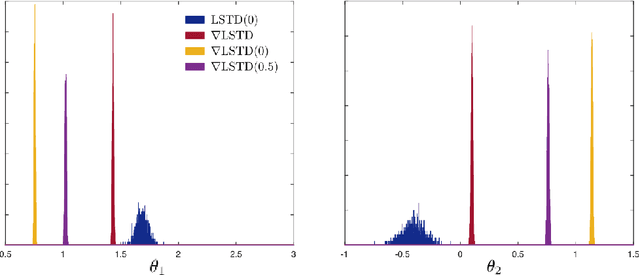
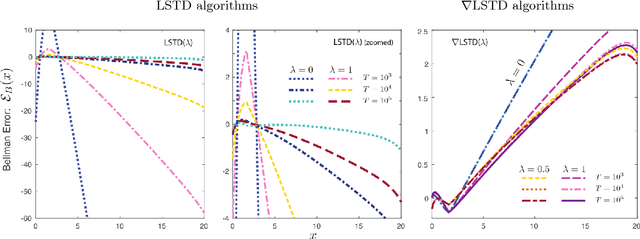
Value functions derived from Markov decision processes arise as a central component of algorithms as well as performance metrics in many statistics and engineering applications of machine learning techniques. Computation of the solution to the associated Bellman equations is challenging in most practical cases of interest. A popular class of approximation techniques, known as Temporal Difference (TD) learning algorithms, are an important sub-class of general reinforcement learning methods. The algorithms introduced in this paper are intended to resolve two well-known difficulties of TD-learning approaches: Their slow convergence due to very high variance, and the fact that, for the problem of computing the relative value function, consistent algorithms exist only in special cases. First we show that the gradients of these value functions admit a representation that lends itself to algorithm design. Based on this result, a new class of differential TD-learning algorithms is introduced. For Markovian models on Euclidean space with smooth dynamics, the algorithms are shown to be consistent under general conditions. Numerical results show dramatic variance reduction when compared to standard methods.