The Bayesian Context Trees State Space Model for time series modelling and forecasting

A hierarchical Bayesian framework is introduced for developing rich mixture models for real-valued time series, along with a collection of effective tools for learning and inference. At the top level, meaningful discrete states are identified as appropriately quantised values of some of the most recent samples. This collection of observable states is described as a discrete context-tree model. Then, at the bottom level, a different, arbitrary model for real-valued time series - a base model - is associated with each state. This defines a very general framework that can be used in conjunction with any existing model class to build flexible and interpretable mixture models. We call this the Bayesian Context Trees State Space Model, or the BCT-X framework. Efficient algorithms are introduced that allow for effective, exact Bayesian inference; in particular, the maximum a posteriori probability (MAP) context-tree model can be identified. These algorithms can be updated sequentially, facilitating efficient online forecasting. The utility of the general framework is illustrated in two particular instances: When autoregressive (AR) models are used as base models, resulting in a nonlinear AR mixture model, and when conditional heteroscedastic (ARCH) models are used, resulting in a mixture model that offers a powerful and systematic way of modelling the well-known volatility asymmetries in financial data. In forecasting, the BCT-X methods are found to outperform state-of-the-art techniques on simulated and real-world data, both in terms of accuracy and computational requirements. In modelling, the BCT-X structure finds natural structure present in the data. In particular, the BCT-ARCH model reveals a novel, important feature of stock market index data, in the form of an enhanced leverage effect.

Change-point Detection and Segmentation of Discrete Data using Bayesian Context Trees

A new Bayesian modelling framework is introduced for piece-wise homogeneous variable-memory Markov chains, along with a collection of effective algorithmic tools for change-point detection and segmentation of discrete time series. Building on the recently introduced Bayesian Context Trees (BCT) framework, the distributions of different segments in a discrete time series are described as variable-memory Markov chains. Inference for the presence and location of change-points is then performed via Markov chain Monte Carlo sampling. The key observation that facilitates effective sampling is that, using one of the BCT algorithms, the prior predictive likelihood of the data can be computed exactly, integrating out all the models and parameters in each segment. This makes it possible to sample directly from the posterior distribution of the number and location of the change-points, leading to accurate estimates and providing a natural quantitative measure of uncertainty in the results. Estimates of the actual model in each segment can also be obtained, at essentially no additional computational cost. Results on both simulated and real-world data indicate that the proposed methodology performs better than or as well as state-of-the-art techniques.

Hierarchical Bayesian Mixture Models for Time Series Using Context Trees as State Space Partitions

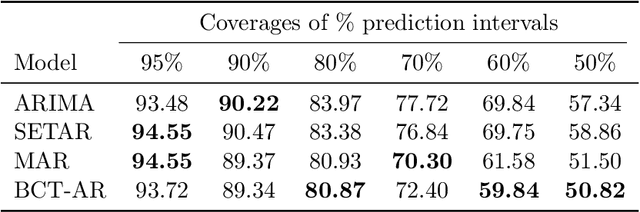
A general Bayesian framework is introduced for mixture modelling and inference with real-valued time series. At the top level, the state space is partitioned via the choice of a discrete context tree, so that the resulting partition depends on the values of some of the most recent samples. At the bottom level, a different model is associated with each region of the partition. This defines a very rich and flexible class of mixture models, for which we provide algorithms that allow for efficient, exact Bayesian inference. In particular, we show that the maximum a posteriori probability (MAP) model (including the relevant MAP context tree partition) can be precisely identified, along with its exact posterior probability. The utility of this general framework is illustrated in detail when a different autoregressive (AR) model is used in each state-space region, resulting in a mixture-of-AR model class. The performance of the associated algorithmic tools is demonstrated in the problems of model selection and forecasting on both simulated and real-world data, where they are found to provide results as good or better than state-of-the-art methods.