Convex Q-Learning, Part 1: Deterministic Optimal Control

It is well known that the extension of Watkins' algorithm to general function approximation settings is challenging: does the projected Bellman equation have a solution? If so, is the solution useful in the sense of generating a good policy? And, if the preceding questions are answered in the affirmative, is the algorithm consistent? These questions are unanswered even in the special case of Q-function approximations that are linear in the parameter. The challenge seems paradoxical, given the long history of convex analytic approaches to dynamic programming. The paper begins with a brief survey of linear programming approaches to optimal control, leading to a particular over parameterization that lends itself to applications in reinforcement learning. The main conclusions are summarized as follows: (i) The new class of convex Q-learning algorithms is introduced based on the convex relaxation of the Bellman equation. Convergence is established under general conditions, including a linear function approximation for the Q-function. (ii) A batch implementation appears similar to the famed DQN algorithm (one engine behind AlphaZero). It is shown that in fact the algorithms are very different: while convex Q-learning solves a convex program that approximates the Bellman equation, theory for DQN is no stronger than for Watkins' algorithm with function approximation: (a) it is shown that both seek solutions to the same fixed point equation, and (b) the ODE approximations for the two algorithms coincide, and little is known about the stability of this ODE. These results are obtained for deterministic nonlinear systems with total cost criterion. Many extensions are proposed, including kernel implementation, and extension to MDP models.

Q-learning with Uniformly Bounded Variance: Large Discounting is Not a Barrier to Fast Learning

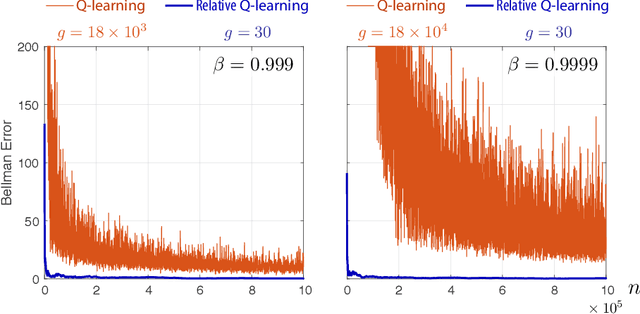
It has been a trend in the Reinforcement Learning literature to derive sample complexity bounds: a bound on how many experiences with the environment are required to obtain an $\varepsilon$-optimal policy. In the discounted cost, infinite horizon setting, all of the known bounds have a factor that is a polynomial in $1/(1-\beta)$, where $\beta < 1$ is the discount factor. For a large discount factor, these bounds seem to imply that a very large number of samples is required to achieve an $\varepsilon$-optimal policy. The objective of the present work is to introduce a new class of algorithms that have sample complexity uniformly bounded for all $\beta < 1$. One may argue that this is impossible, due to a recent min-max lower bound. The explanation is that this previous lower bound is for a specific problem, which we modify, without compromising the ultimate objective of obtaining an $\varepsilon$-optimal policy. Specifically, we show that the asymptotic variance of the Q-learning algorithm, with an optimized step-size sequence, is a quadratic function of $1/(1-\beta)$; an expected, and essentially known result. The new relative Q-learning algorithm proposed here is shown to have asymptotic variance that is a quadratic in $1/(1- \rho \beta)$, where $1 - \rho > 0$ is the spectral gap of an optimal transition matrix.

Zap Q-Learning for Optimal Stopping Time Problems

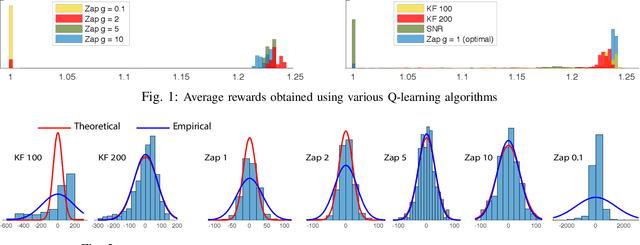
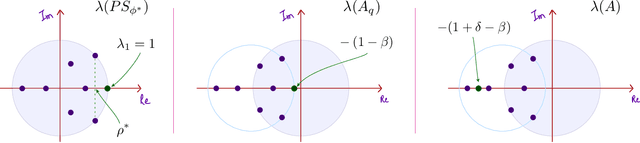
We propose a novel reinforcement learning algorithm that approximates solutions to the problem of discounted optimal stopping in an irreducible, uniformly ergodic Markov chain evolving on a compact subset of $\mathbb R^n$. A dynamic programming approach has been taken by Tsitsikilis and Van Roy to solve this problem, wherein they propose a Q-learning algorithm to estimate the value function, in a linear function approximation setting. The Zap-Q learning algorithm proposed in this work is the first algorithm that is designed to achieve optimal asymptotic variance. We prove convergence of the algorithm using ODE analysis, and the optimal asymptotic variance property is reflected via fast convergence in a finance example.

Differential Temporal Difference Learning

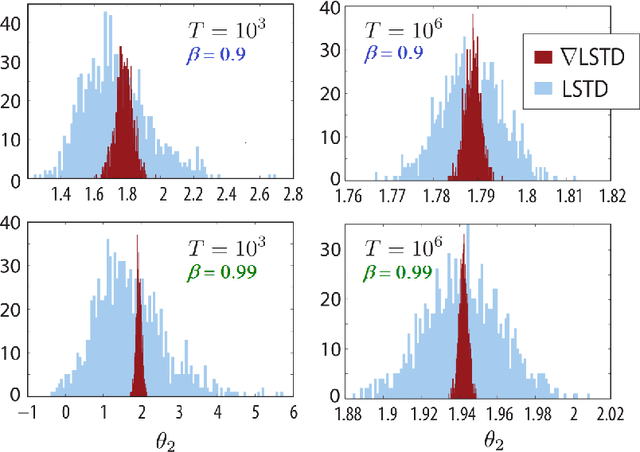
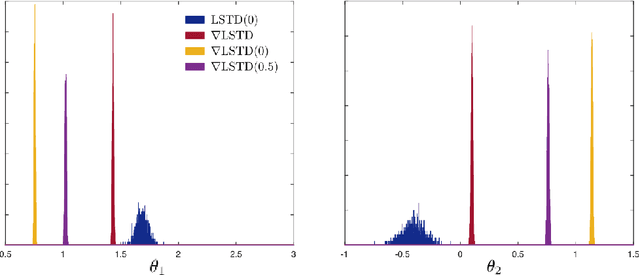
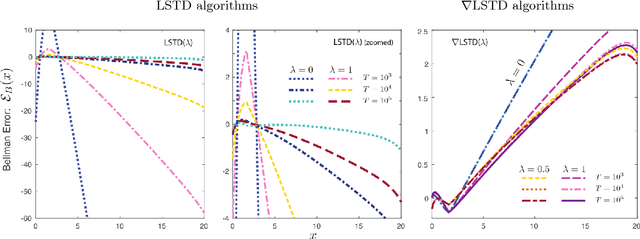
Value functions derived from Markov decision processes arise as a central component of algorithms as well as performance metrics in many statistics and engineering applications of machine learning techniques. Computation of the solution to the associated Bellman equations is challenging in most practical cases of interest. A popular class of approximation techniques, known as Temporal Difference (TD) learning algorithms, are an important sub-class of general reinforcement learning methods. The algorithms introduced in this paper are intended to resolve two well-known difficulties of TD-learning approaches: Their slow convergence due to very high variance, and the fact that, for the problem of computing the relative value function, consistent algorithms exist only in special cases. First we show that the gradients of these value functions admit a representation that lends itself to algorithm design. Based on this result, a new class of differential TD-learning algorithms is introduced. For Markovian models on Euclidean space with smooth dynamics, the algorithms are shown to be consistent under general conditions. Numerical results show dramatic variance reduction when compared to standard methods.

Fastest Convergence for Q-learning

The Zap Q-learning algorithm introduced in this paper is an improvement of Watkins' original algorithm and recent competitors in several respects. It is a matrix-gain algorithm designed so that its asymptotic variance is optimal. Moreover, an ODE analysis suggests that the transient behavior is a close match to a deterministic Newton-Raphson implementation. This is made possible by a two time-scale update equation for the matrix gain sequence. The analysis suggests that the approach will lead to stable and efficient computation even for non-ideal parameterized settings. Numerical experiments confirm the quick convergence, even in such non-ideal cases. A secondary goal of this paper is tutorial. The first half of the paper contains a survey on reinforcement learning algorithms, with a focus on minimum variance algorithms.

Differential TD Learning for Value Function Approximation

Value functions arise as a component of algorithms as well as performance metrics in statistics and engineering applications. Computation of the associated Bellman equations is numerically challenging in all but a few special cases. A popular approximation technique is known as Temporal Difference (TD) learning. The algorithm introduced in this paper is intended to resolve two well-known problems with this approach:In the discounted-cost setting, the variance of the algorithm diverges as the discount factor approaches unity. Second, for the average cost setting, unbiased algorithms exist only in special cases. It is shown that the gradient of any of these value functions admits a representation that lends itself to algorithm design. Based on this result, the new differential TD method is obtained for Markovian models on Euclidean space with smooth dynamics. Numerical examples show remarkable improvements in performance. In application to speed scaling, variance is reduced by two orders of magnitude.