Neural Models and Algorithms for Sensorimotor Control of an Octopus Arm

In this article, a biophysically realistic model of a soft octopus arm with internal musculature is presented. The modeling is motivated by experimental observations of sensorimotor control where an arm localizes and reaches a target. Major contributions of this article are: (i) development of models to capture the mechanical properties of arm musculature, the electrical properties of the arm peripheral nervous system (PNS), and the coupling of PNS with muscular contractions; (ii) modeling the arm sensory system, including chemosensing and proprioception; and (iii) algorithms for sensorimotor control, which include a novel feedback neural motor control law for mimicking target-oriented arm reaching motions, and a novel consensus algorithm for solving sensing problems such as locating a food source from local chemical sensory information (exogenous) and arm deformation information (endogenous). Several analytical results, including rest-state characterization and stability properties of the proposed sensing and motor control algorithms, are provided. Numerical simulations demonstrate the efficacy of our approach. Qualitative comparisons against observed arm rest shapes and target-oriented reaching motions are also reported.

Topology, dynamics, and control of an octopus-analog muscular hydrostat

Muscular hydrostats, such as octopus arms or elephant trunks, lack bones entirely, endowing them with exceptional dexterity and reconfigurability. Key to their unmatched ability to control nearly infinite degrees of freedom is the architecture into which muscle fibers are weaved. Their arrangement is, effectively, the instantiation of a sophisticated mechanical program that mediates, and likely facilitates, the control and realization of complex, dynamic morphological reconfigurations. Here, by combining medical imaging, biomechanical data, live behavioral experiments and numerical simulations, we synthesize a model octopus arm entailing ~200 continuous muscles groups, and begin to unravel its complexity. We show how 3D arm motions can be understood in terms of storage, transport, and conversion of topological quantities, effected by simple muscle activation templates. These, in turn, can be composed into higher-level control strategies that, compounded by the arm's compliance, are demonstrated in a range of object manipulation tasks rendered additionally challenging by the need to appropriately align suckers, to sense and grasp. Overall, our work exposes broad design and algorithmic principles pertinent to muscular hydrostats, robotics, and dynamics, while significantly advancing our ability to model muscular structures from medical imaging, with potential implications for human health and care.

Hierarchical control and learning of a foraging CyberOctopus

Inspired by the unique neurophysiology of the octopus, we propose a hierarchical framework that simplifies the coordination of multiple soft arms by decomposing control into high-level decision making, low-level motor activation, and local reflexive behaviors via sensory feedback. When evaluated in the illustrative problem of a model octopus foraging for food, this hierarchical decomposition results in significant improvements relative to end-to-end methods. Performance is achieved through a mixed-modes approach, whereby qualitatively different tasks are addressed via complementary control schemes. Here, model-free reinforcement learning is employed for high-level decision-making, while model-based energy shaping takes care of arm-level motor execution. To render the pairing computationally tenable, a novel neural-network energy shaping (NN-ES) controller is developed, achieving accurate motions with time-to-solutions 200 times faster than previous attempts. Our hierarchical framework is then successfully deployed in increasingly challenging foraging scenarios, including an arena littered with obstacles in 3D space, demonstrating the viability of our approach.

Modeling the Neuromuscular Control System of an Octopus Arm

The octopus arm is a neuromechanical system that involves a complex interplay between peripheral nervous system (PNS) and arm musculature. This makes the arm capable of carrying out rich maneuvers. In this paper, we build a model for the PNS and integrate it with a muscular soft octopus arm. The proposed neuromuscular architecture is used to qualitatively reproduce several biophysical observations in real octopuses, including curled rest shapes and target-directed arm reaching motions. Two control laws are proposed for target-oriented arm motions, and their performance is compared against a benchmark. Several analytical results, including rest-state characterization and stability properties of the proposed control laws, are provided.

Energy Shaping Control of a Muscular Octopus Arm Moving in Three Dimensions

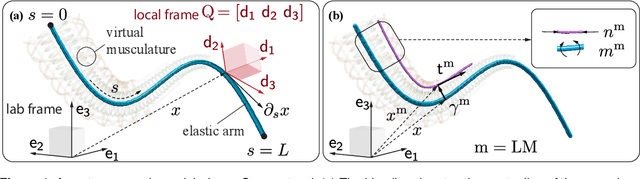
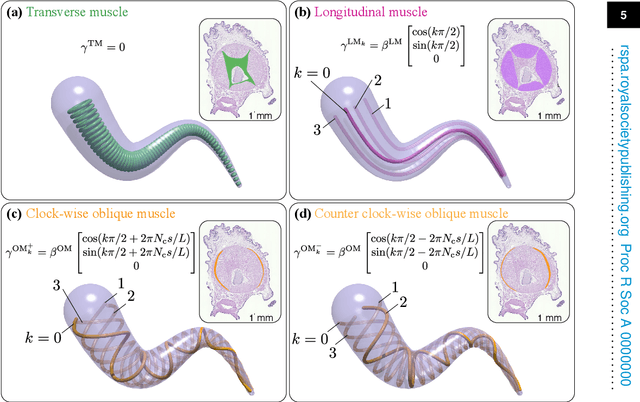
Flexible octopus arms exhibit an exceptional ability to coordinate large numbers of degrees of freedom and perform complex manipulation tasks. As a consequence, these systems continue to attract the attention of biologists and roboticists alike. In this paper, we develop a three-dimensional model of a soft octopus arm, equipped with biomechanically realistic muscle actuation. Internal forces and couples exerted by all major muscle groups are considered. An energy shaping control method is described to coordinate muscle activity so as to grasp and reach in 3D space. Key contributions of this paper are: (i) modeling of major muscle groups to elicit three-dimensional movements; (ii) a mathematical formulation for muscle activations based on a stored energy function; and (iii) a computationally efficient procedure to design task-specific equilibrium configurations, obtained by solving an optimization problem in the Special Euclidean group SE(3). Muscle controls are then iteratively computed based on the co-state variable arising from the solution of the optimization problem. The approach is numerically demonstrated in the physically accurate software environment Elastica. Results of numerical experiments mimicking observed octopus behaviors are reported.

A Sensory Feedback Control Law for Octopus Arm Movements

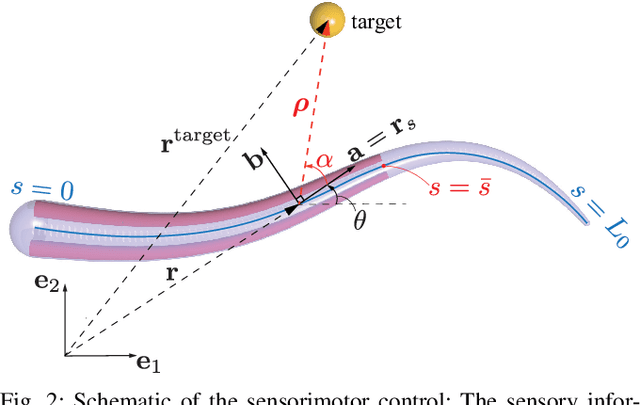
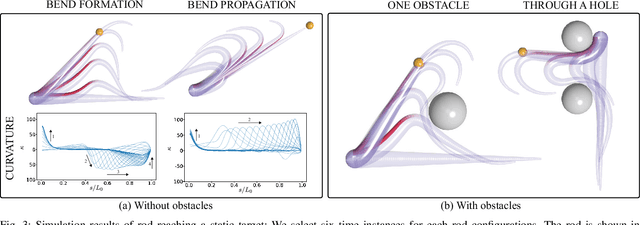
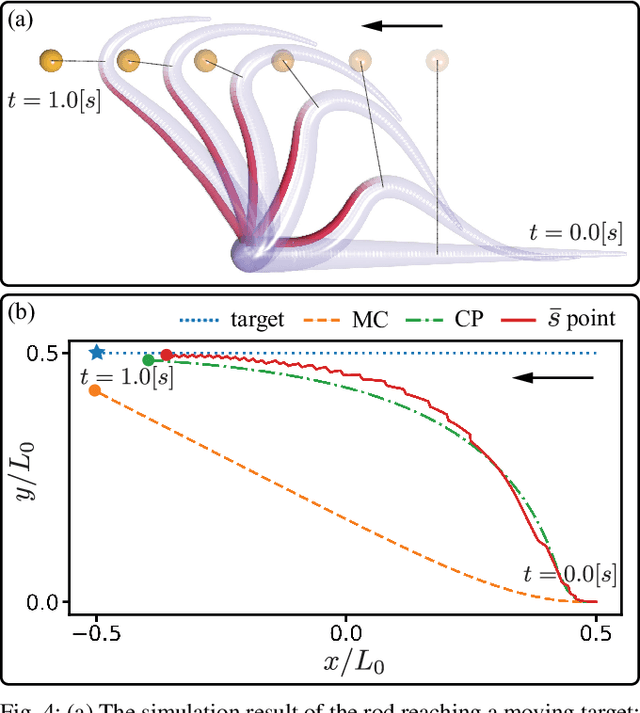
The main contribution of this paper is a novel sensory feedback control law for an octopus arm. The control law is inspired by, and helps integrate, several observations made by biologists. The proposed control law is distinct from prior work which has mainly focused on open-loop control strategies. Several analytical results are described including characterization of the equilibrium and its stability analysis. Numerical simulations demonstrate life-like motion of the soft octopus arm, qualitatively matching behavioral experiments. Quantitative comparison with bend propagation experiments helps provide the first explanation of such canonical motion using a sensory feedback control law. Several remarks are included that help draw parallels with natural pursuit strategies such as motion camouflage or classical pursuit.

A physics-informed, vision-based method to reconstruct all deformation modes in slender bodies

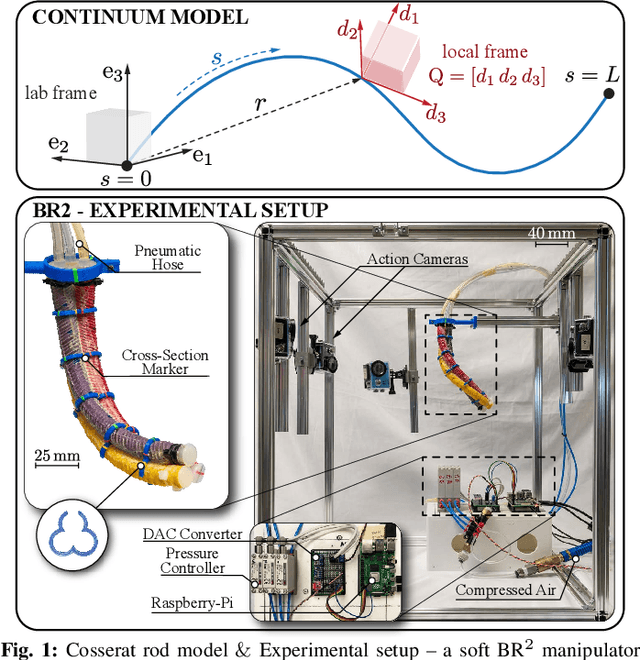
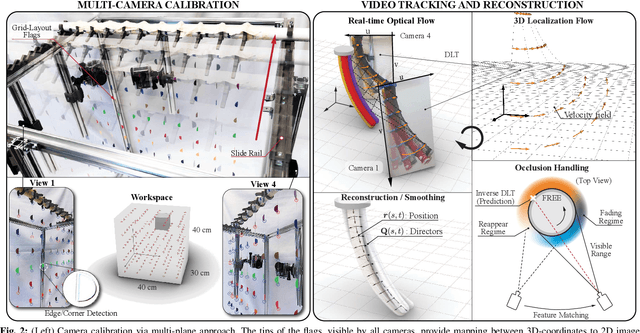
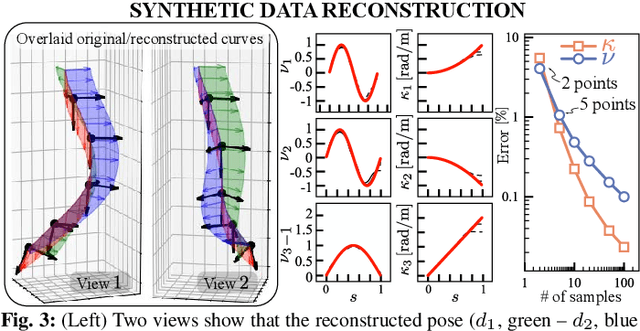
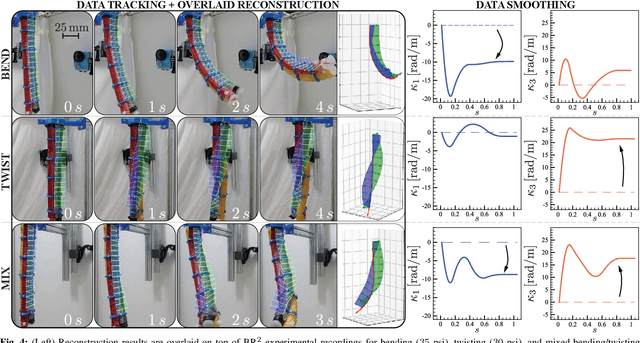
This paper is concerned with the problem of estimating (interpolating and smoothing) the shape (pose and the six modes of deformation) of a slender flexible body from multiple camera measurements. This problem is important in both biology, where slender, soft, and elastic structures are ubiquitously encountered across species, and in engineering, particularly in the area of soft robotics. The proposed mathematical formulation for shape estimation is physics-informed, based on the use of the special Cosserat rod theory whose equations encode slender body mechanics in the presence of bending, shearing, twisting and stretching. The approach is used to derive numerical algorithms which are experimentally demonstrated for fiber reinforced and cable-driven soft robot arms. These experimental demonstrations show that the methodology is accurate (<5 mm error, three times less than the arm diameter) and robust to noise and uncertainties.

Optimal Control of a Soft CyberOctopus Arm

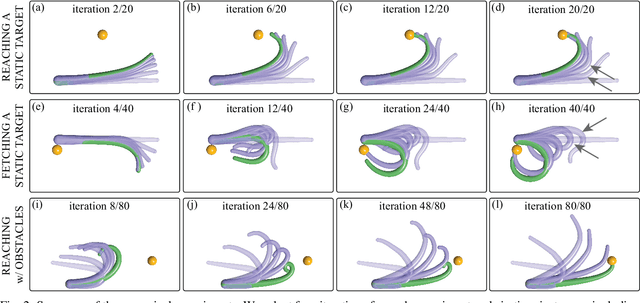
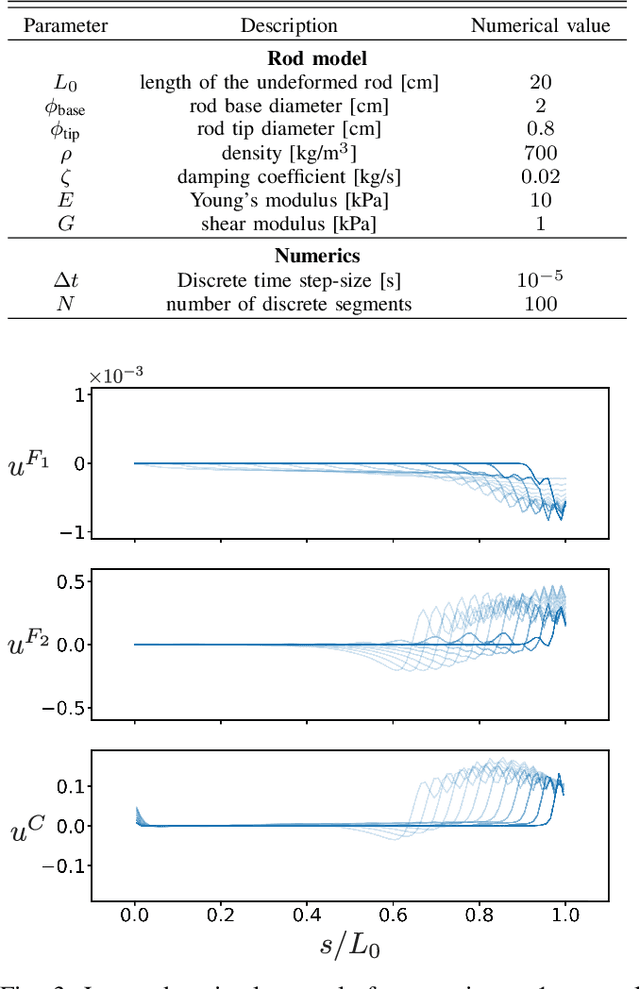
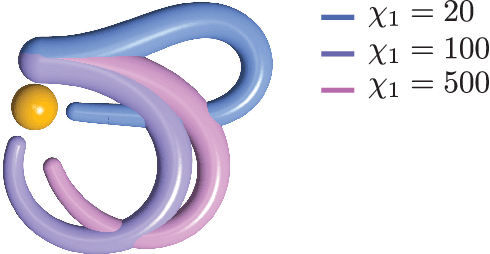
In this paper, we use the optimal control methodology to control a flexible, elastic Cosserat rod. An inspiration comes from stereotypical movement patterns in octopus arms, which are observed in a variety of manipulation tasks, such as reaching or fetching. To help uncover the mechanisms underlying these observed behaviors, we outline an optimal control-based framework. A single octopus arm is modeled as a Hamiltonian control system, where the continuum mechanics of the arm is captured by the Cosserat rod theory, and internal, distributed muscle forces and couples are considered as controls. First order necessary optimality conditions are derived for an optimal control problem formulated for this infinite dimensional system. Solutions to this problem are obtained numerically by an iterative forward-backward algorithm. The state and adjoint equations are solved in a dynamic simulation environment, setting the stage for studying a broader class of optimal control problems. Trajectories that minimize control effort are demonstrated and qualitatively compared with observed behaviors.

Controlling a CyberOctopus Soft Arm with Muscle-like Actuation

This paper entails the application of the energy shaping methodology to control a flexible, elastic Cosserat rod model of a single octopus arm. The principal focus and novel contribution of this work is two-fold: (i) reduced order control oriented modeling of the realistic internal muscular architecture in an octopus arm; and (ii) incorporation of such models into the energy shaping methodology, extending our prior work by formally accounting for muscle constraints. Extension of the control scheme to the under-actuated muscle control case involves two steps: (i) design of a desired potential energy function whose static minimizer solves a given control task; and (ii) implementing the resulting energy shaping control input into the dynamic model. Due to the muscle actuator constraints, the desired potential energy function may not be arbitrarily chosen. Indeed, the desired energy must now satisfy a partial differential equation, known as the matching condition, which is derived for the infinite dimensional Hamiltonian control system. A particular solution to those matching conditions is described, paving the way to the application of energy shaping methodology. The overall control design methodology including muscle models is implemented and demonstrated in a dynamic simulation environment. Results of several bio-inspired numerical experiments involving the control of octopus arms are reported.

Deep FPF: Gain function approximation in high-dimensional setting

In this paper, we present a novel approach to approximate the gain function of the feedback particle filter (FPF). The exact gain function is the solution of a Poisson equation involving a probability-weighted Laplacian. The numerical problem is to approximate the exact gain function using only finitely many particles sampled from the probability distribution. Inspired by the recent success of the deep learning methods, we represent the gain function as a gradient of the output of a neural network. Thereupon considering a certain variational formulation of the Poisson equation, an optimization problem is posed for learning the weights of the neural network. A stochastic gradient algorithm is described for this purpose. The proposed approach has two significant properties/advantages: (i) The stochastic optimization algorithm allows one to process, in parallel, only a batch of samples (particles) ensuring good scaling properties with the number of particles; (ii) The remarkable representation power of neural networks means that the algorithm is potentially applicable and useful to solve high-dimensional problems. We numerically establish these two properties and provide extensive comparison to the existing approaches.