Topology, dynamics, and control of an octopus-analog muscular hydrostat

Muscular hydrostats, such as octopus arms or elephant trunks, lack bones entirely, endowing them with exceptional dexterity and reconfigurability. Key to their unmatched ability to control nearly infinite degrees of freedom is the architecture into which muscle fibers are weaved. Their arrangement is, effectively, the instantiation of a sophisticated mechanical program that mediates, and likely facilitates, the control and realization of complex, dynamic morphological reconfigurations. Here, by combining medical imaging, biomechanical data, live behavioral experiments and numerical simulations, we synthesize a model octopus arm entailing ~200 continuous muscles groups, and begin to unravel its complexity. We show how 3D arm motions can be understood in terms of storage, transport, and conversion of topological quantities, effected by simple muscle activation templates. These, in turn, can be composed into higher-level control strategies that, compounded by the arm's compliance, are demonstrated in a range of object manipulation tasks rendered additionally challenging by the need to appropriately align suckers, to sense and grasp. Overall, our work exposes broad design and algorithmic principles pertinent to muscular hydrostats, robotics, and dynamics, while significantly advancing our ability to model muscular structures from medical imaging, with potential implications for human health and care.

Controlling a CyberOctopus Soft Arm with Muscle-like Actuation

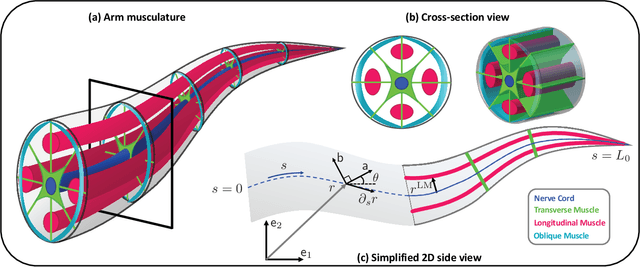
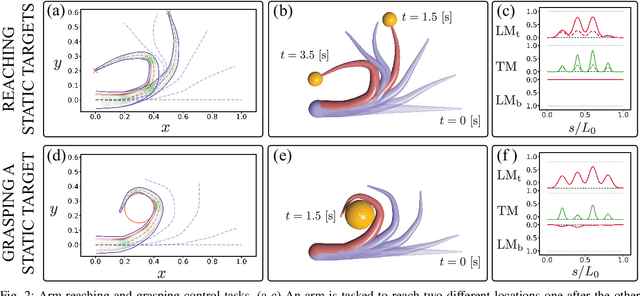
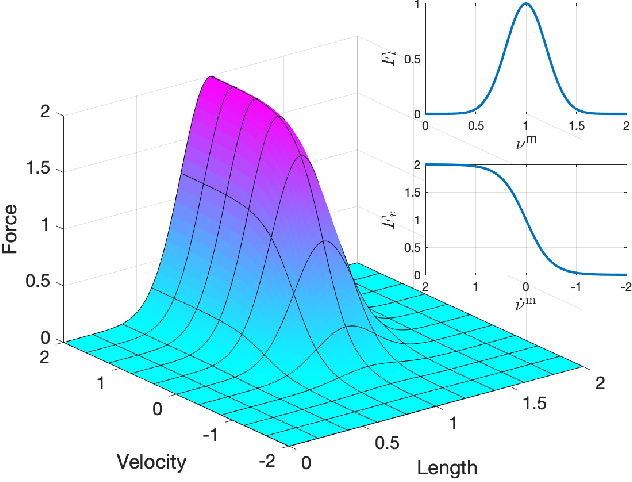
This paper entails the application of the energy shaping methodology to control a flexible, elastic Cosserat rod model of a single octopus arm. The principal focus and novel contribution of this work is two-fold: (i) reduced order control oriented modeling of the realistic internal muscular architecture in an octopus arm; and (ii) incorporation of such models into the energy shaping methodology, extending our prior work by formally accounting for muscle constraints. Extension of the control scheme to the under-actuated muscle control case involves two steps: (i) design of a desired potential energy function whose static minimizer solves a given control task; and (ii) implementing the resulting energy shaping control input into the dynamic model. Due to the muscle actuator constraints, the desired potential energy function may not be arbitrarily chosen. Indeed, the desired energy must now satisfy a partial differential equation, known as the matching condition, which is derived for the infinite dimensional Hamiltonian control system. A particular solution to those matching conditions is described, paving the way to the application of energy shaping methodology. The overall control design methodology including muscle models is implemented and demonstrated in a dynamic simulation environment. Results of several bio-inspired numerical experiments involving the control of octopus arms are reported.

Elastica: A compliant mechanics environment for soft robotic control

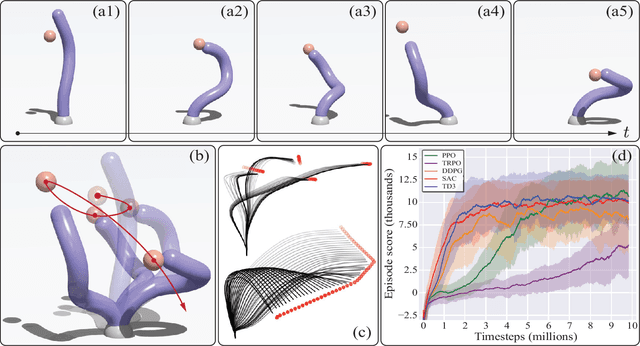
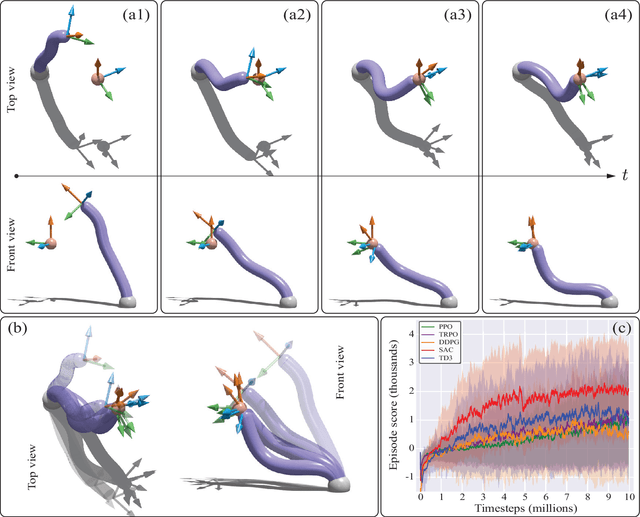
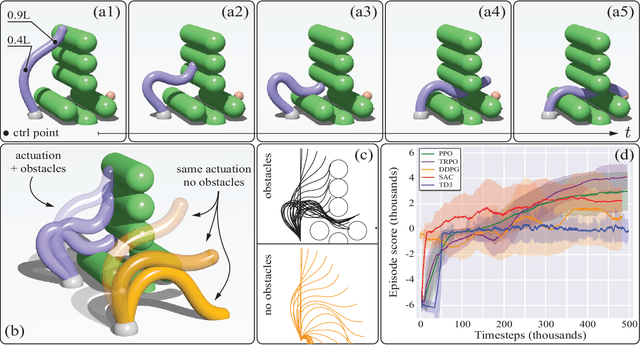
Soft robots are notoriously hard to control. This is partly due to the scarcity of models able to capture their complex continuum mechanics, resulting in a lack of control methodologies that take full advantage of body compliance. Currently available simulation methods are either too computational demanding or overly simplistic in their physical assumptions, leading to a paucity of available simulation resources for developing such control schemes. To address this, we introduce Elastica, a free, open-source simulation environment for soft, slender rods that can bend, twist, shear and stretch. We demonstrate how Elastica can be coupled with five state-of-the-art reinforcement learning algorithms to successfully control a soft, compliant robotic arm and complete increasingly challenging tasks.

Energy Shaping Control of a CyberOctopus Soft Arm

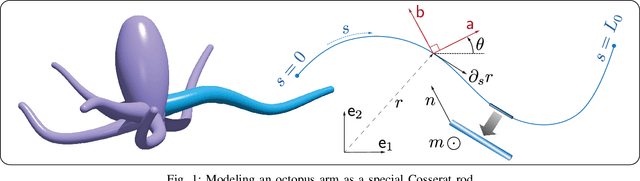
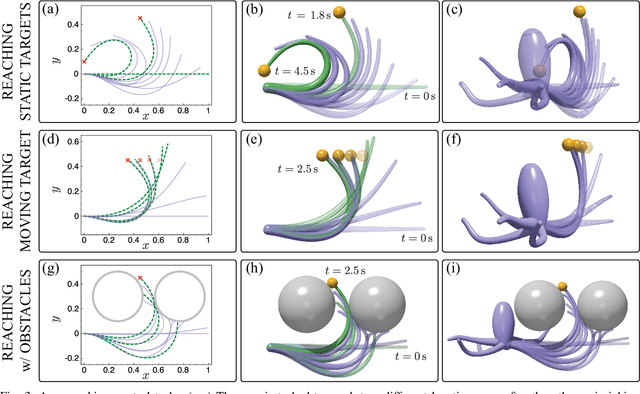
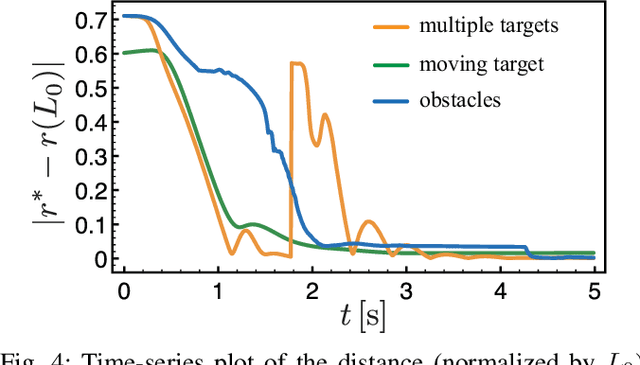
This paper entails application of the energy shaping methodology to control a flexible, elastic Cosserat rod model. Recent interest in such continuum models stems from applications in soft robotics, and from the growing recognition of the role of mechanics and embodiment in biological control strategies: octopuses are often regarded as iconic examples of this interplay. Here, the dynamics of the Cosserat rod, modeling a single octopus arm, are treated as a Hamiltonian system and the internal muscle actuators are modeled as distributed forces and couples. The proposed energy shaping control design procedure involves two steps: (1) a potential energy is designed such that its minimizer is the desired equilibrium configuration; (2) an energy shaping control law is implemented to reach the desired equilibrium. By interpreting the controlled Hamiltonian as a Lyapunov function, asymptotic stability of the equilibrium configuration is deduced. The energy shaping control law is shown to require only the deformations of the equilibrium configuration. A forward-backward algorithm is proposed to compute these deformations in an online iterative manner. The overall control design methodology is implemented and demonstrated in a dynamic simulation environment. Results of several bio-inspired numerical experiments involving the control of octopus arms are reported.